
- •Московский государственный университет путей сообщения рф (миит) Кафедра «Физика-2»
- •Отчёт по лабораторной работе № 29 изучение затухающих электромагнитных колебаний в колебательном контуре с помощью осциллографа
- •3. Основные теоретические положения к данной работе
- •4. Установим некоторые значения индуктивности и емкости в контуре, учитывая, что при последовательном соединении lоб l1 l2, cоб с1с2/(c1 c2).
- •5. Расчёт погрешностей измерений
- •6. Окончательные результаты:
- •7. Дополнительная страница
Московский государственный университет путей сообщения рф (миит) Кафедра «Физика-2»
Институт, группа ИТТСУ, ВПЛ-111 К работе допущен __________________
(Дата, подпись преподавателя)
Студент Работа выполнена__________________
(Дата, подпись преподавателя)
Преподаватель Пыканов. И. В. Отчёт принят_______________________ (Дата, подпись преподавателя)
Отчёт по лабораторной работе № 29 изучение затухающих электромагнитных колебаний в колебательном контуре с помощью осциллографа
Цель работы:
Изучение с помощью электронного осциллографа электромагнитных колебаний, возникающих в колебательном контуре, содержащем индуктивность, емкость и активное сопротивление; изучение условий возникновения затухающих колебаний в контуре; расчет основных физических величин, характеризующих эти колебания.
П
 риборы
и принадлежности:
панель с колебательным контуром, магазин
сопротивлений, электронный осциллограф,
соединительные провода
риборы
и принадлежности:
панель с колебательным контуром, магазин
сопротивлений, электронный осциллограф,
соединительные провода
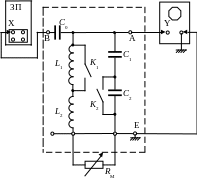
Y – Осциллограф.
ЗП – Задняя панель осциллографа.
Rm – Магазин сопротивлений.
LC – Колебательный контур.
3. Основные теоретические положения к данной работе
В данной работе мы изучим работу электромагнитных колебаний, возникающих в колебательном контуре, содержащем индуктивность, емкость и активное сопротивление.
На рис. 1 изображена электрическая схема простейшего колебательного контура с сосредоточенными параметрами, содержащего последовательно соединённые конденсатор электроёмкостью C, катушку индуктивностью L и резистор с активным сопротивлением R.
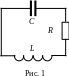
Если в какой-либо момент времени одной из обкладок конденсатора сообщить электрический заряд или создать условия для возникновения в катушке электродвижущей силы (э. д. с.) индукции, а затем отключить источники возбуждения, в контуре начнутся свободные электромагнитные колебания.
Исследуем характер колебаний, возникающих в идеализированном колебательном контуре в отсутствие сопротивления R 0 при сообщении конденсатору заряда q0.
Вначале энергия электрического поля конденсатора емкостью C равна: WC q02/2C CU02/2,
где U0 q0/С - максимальная разность потенциалов на обкладках конденсатора. Под действием электрического поля начинается движение зарядов и конденсатор разряжается. В контуре возникает электрический ток: I(t) – dq(t)/dt, (1)
где dq(t) – изменение заряда на обкладках конденсатора. Знак минус показывает, что возникновение тока сопровождается уменьшением заряда на обкладках конденсатора (dq<0).
Энергия электрического поля конденсатора уменьшается, переходя в энергию магнитного поля, создаваемого током в катушке. Возрастание тока (dI > 0) в катушке индуктивностью L приводит к появлению в ней электродвижущей силы (э. д. с.) самоиндукции Et), препятствующей изменению тока (E < 0): E(t) – L(dI/dt).
При полном разряде конденсатора его электрическое поле исчезает, а ток в контуре, наоборот, достигает максимального значения I0. Максимального значения достигает и энергия магнитного поля в катушке: WL = LI02/2.
С этого момента начинается перезарядка конденсатора под действием э. д. с. самоиндукции. Ток в контуре начинает убывать, вследствие чего э. д. с. самоиндукции изменяет знак, препятствуя убыванию тока. Энергия магнитного поля катушки уменьшается, а энергия электрического поля конденсатора растет, стремясь к максимальному значению, которому соответствует полная перезарядка конденсатора. В тот момент времени мгновенные значения электрического тока и энергии магнитного поля обращаются в нуль. Далее процесс повторяется в обратном порядке. В контуре устанавливаются незатухающие электромагнитные колебания.
Если колебательный контур содержит активное сопротивление R, то при протекании по нему тока часть общей энергии контура W выделяется в виде тепла:
Q WR I2Rt.
При этом уменьшаются с течением времени амплитудные значения тока в контуре и разности потенциалов на обкладках конденсатора. Колебания затухают.
Временная зависимость разности потенциалов на обкладках конденсатора U(t) 1 2 наблюдается в данной работе на экране осциллографа. Эту зависимость можно получить теоретическим путем, используя закон Ома для участка цепи, содержащей э.д.с. Для мгновенных значений токов и напряжений в таком контуре закон Ома запишется в виде:
I
T

Преобразуем это уравнение, используя формулу (1) и соотношение q = CU. Тогда уравнение (2) примет вид:
LC(d2U/dt2) RC(dU/dt) U 0 (3)
Разделив обе части уравнения (3) на LC и введя обозначения R/2L β, 1/LC 02,
где 0 называется собственной циклической (круговой) частотой контура, а – коэффициентом затухания, получим дифференциальное уравнение:
d2U/dt2 2(dU/dt) 02U 0, (4)
решение которого дает искомую зависимость U(t).
Уравнение (4) – линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами. В частном случае, когда < 0, его решение имеет вид:
U(t) U0etcos(t 0), (5)
где 0 – начальная фаза колебаний; – циклическая частота затухающих колебаний:
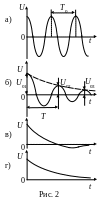
![]()
![]() (6)
(6)
На рис. 2 приведены примеры графиков зависимости U(t) для различных типов колебаний в контуре.
Выражение (5) описывает затухающий колебательный процесс (рис. 2б) с периодом колебаний
T
![]()
 .
(7)
.
(7)
Амплитудой затухающих колебаний называют величину
A(t) U0et, (8)
где U0 – максимально возможное значение амплитуды напряжения: U0 A(t 0).
Как следует из формул (5) и (8), изменение амплитуды колебаний зависит от величины коэффициента затухания . Согласно (8) коэффициент затухания есть физическая величина, обратная времени , в течение которого амплитуда колебаний уменьшается в е раз:
U0/A() e при t 1/.
Таким образом, характер колебательного процесса определяется соотношениями между электрическими параметрами контура R, L и C. Так, при 0 в контуре устанавливаются свободные незатухающие гармонические (колеблющаяся величина изменяется со временем по закону синуса или косинуса) колебания (рис. 2а): U(t) U0cos(0t 0)
с периодом
T0
2/0
2![]() (формула У.Томсона).
(формула У.Томсона).
При критическом сопротивлении (см. формулы (6) и (7))
R
RКР
2![]()
0 и период колебаний становится бесконечным. В контуре возникает апериодический процесс, когда напряжение на конденсаторе постепенно уменьшается, не совершая при этом колебаний (рис. 2в).
При R < RКР (т. е. при < 0) в контуре реализуется затухающий колебательный процесс (рис. 2б).
При R > RКР ( 0) циклическая частота и период колебаний Т становятся мнимыми величинами. Это соответствует апериодическому процессу разряда конденсатора на большое активное сопротивление (рис. 2г).
ln![]()
ln
ln![]()
T
T/
1/N,
(9)
T
T/
1/N,
(9)
т.е. он равен величине, обратной числу колебаний (периодов), за которое амплитуда уменьшается в е раз (N ).
Добротность контура Q – важный параметр, характеризующий быстроту потери энергии, запасенной в контуре. Добротность контура показывает, во сколько раз амплитуда вынужденных колебаний напряжения на конденсаторе при резонансе превышает амплитуду внешней прикладываемой электродвижущей силы, и определяется формулой: Q 0/2.
Для колебаний при малых частота затухающих колебаний ω приблизительно равна собственной частоте колебаний 0 (см. формулу (6)) и тогда, учитывая формулу (9), величина добротности:
Q 0/2 ≈ /2 = 2/2βT /.
Для
колебательного контура: R/2L,
и 0
1/![]() .
.
Добротность в этом случае:
Q
0/2
![]()
/R.
(10)
/R.
(10)
Физическую
величину
![]() называют волновым или характеристическим
сопротивлением колебательного контура.
называют волновым или характеристическим
сопротивлением колебательного контура.
Схема установки и способы возбуждения и наблюдения колебаний
Колебательный контур состоит из последовательно соединенных конденсаторов С1 и C2 катушек L1 и L2 , магазина сопротивлений RМ. Значения емкостей С1 и C2, индуктивностей L1 и L2 , а также величины активного сопротивления катушек RL и других элементов цепи RЦ указаны на панели контура. С помощью ключей К1 и К2 можно изменять величины емкости и индуктивности контура. Разделительный конденсатор C0 в контур не входит и его электроемкость при расчетах не учитывается.
Для возбуждения колебаний в данной работе используется пилообразное напряжение генератора развертки луча осциллографа. Напряжение U снимается с выхода X-пластин, расположенного на задней панели (ЗП – рис. 3) осциллографа, и подается к клемме B колебательного контура, перераспределяясь между конденсаторами С0, С1 и С2. Поскольку в схеме подобрано С0 << С1 и С0 << С2, то
U UС0 UС1 UС2 q/C0 q/C1 q/C2 q/C0 UС0,
т. е. все напряжение падает почти полностью на конденсаторе С0.
При линейном возрастании пилообразного напряжения развертки линейно возрастает напряжение на конденсаторе С0: UC0 at (рис. 4а, участок ab).
и, следовательно, на участке ab линейно возрастающего напряжения э. д. с. самоиндукции в катушках L1, L2 не возникает: Et) L(dI/dt) 0.
В момент начала быстрого нелинейного спада пилообразного напряжения (участок bc) dUC0/dt изменяется, т. е. и ток разрядки конденсатора С0 непостоянен (I const), а следовательно, в катушках L1, L2 возникает э. д. с.: Et) L(dI/dt) ≠ 0,
к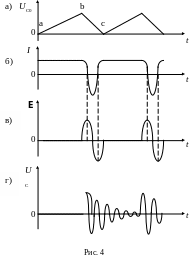 оторая
и является источником энергии, вызывающим
появление затухающих колебаний (например,
напряжения UС
на конденсаторах С1,
и C2
(рис. 4г). Возникающие в контуре затухающие
колебания (рис. 4г) будут
продолжаться и во время следующего
периода нарастания напряжения развертки,
смещающего луч по горизонтальной оси
(X)
экрана осциллографа. Их можно наблюдать
на экране осциллографа при подаче
напряжения UС
(клемма
А контура) на вход Y
осциллографа. Клемма «вход Y»
расположена на передней панели
осциллографа. Клемма Е («земля») контура
соединяется с соответствующей клеммой
осциллографа. Устойчивое изображение
затухающих колебаний можно получить
на экране осциллографа при правильном
подборе частоты развертки, частоты
синхронизации, усиления сигнала по
вертикальной (Y)
и горизонтальной (X)
осям.
оторая
и является источником энергии, вызывающим
появление затухающих колебаний (например,
напряжения UС
на конденсаторах С1,
и C2
(рис. 4г). Возникающие в контуре затухающие
колебания (рис. 4г) будут
продолжаться и во время следующего
периода нарастания напряжения развертки,
смещающего луч по горизонтальной оси
(X)
экрана осциллографа. Их можно наблюдать
на экране осциллографа при подаче
напряжения UС
(клемма
А контура) на вход Y
осциллографа. Клемма «вход Y»
расположена на передней панели
осциллографа. Клемма Е («земля») контура
соединяется с соответствующей клеммой
осциллографа. Устойчивое изображение
затухающих колебаний можно получить
на экране осциллографа при правильном
подборе частоты развертки, частоты
синхронизации, усиления сигнала по
вертикальной (Y)
и горизонтальной (X)
осям.
Порядок выполнения работы
1. Собираем схему установки в соответствии с рис. 3.
2. Подключим осциллограф к внешней сети и включим тумблер «сеть», дадим прогреться 2 – 3 мин и отрегулируем яркость и фокусировку луча. Переключатель «синхронизация» ставим в положение «внутр.», тумблер «делитель» на передней панели осциллографа в положение «до 5 В».
3. Устанавливаем на магазине сопротивлений RМ 0. С помощью ручек усиления и установки частоты развертки и синхронизации осциллографа получаем на экране устойчивое изображение затухающих колебаний.
Варьируя с помощью ключей К1 и К2 величины L и С контура, наблюдаем за изменением характера колебаний.
