6 Случайные процессы

6.1 Понятие случайного процесса

При изучении многих явлений природы приходится встречаться с процессами, течение которых заранее предсказать невозможно. Эта непредсказуемость вызвана влиянием случайных факторов, воздействующих на ход процесса. Примерами случайных процессов являются: траектории частиц в броуновском движении, траектория полета летательного аппарата, флуктуационные шумы в радиоэлектронной аппаратуре, изменение температуры больного в ходе болезни, вибрация узлов станка во время его работы и т. д.

Случайный процесс описывается случайной функцией времени x(t), мгновенные значения которой в любые моменты времени являются случайными величинами.

Случайной функцией X(t) называют функцию, которая в результате опыта может принять тот или иной вид, причем заранее неизвестно какой именно.

Случайная величина X(t0), в которую обращается случайный процесс при t=t0, называется сечением случайного процесса, соответствующим данному значению аргумента t.

Конкретный вид, который принимает случайный процесс в результате опыта, называется реализацией случайного процесса.

Реализацией случайного процесса X(t) будем называть неслучайную функцию x(t), в которую превращается случайный процесс X(t) в результате опыта.

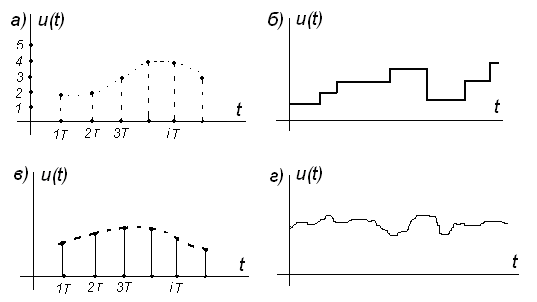
Рисунок 6.1 – Реализации случайных процессов

Реализации случайного процесса могут иметь как непрерывную, так и дискретную структуру. По своей структуре все случайные процессы делят на четыре класса:

процессы с дискретными состояниями и с дискретным временем (рис.6.1а);

процессы с дискретными состояниями и с непрерывным временем (рис.6.1б);

процессы с непрерывными состояниями и с дискретными временем (рис.6.1в);

процессы с непрерывными состояниями и с непрерывным временем (рис.6.1г).

В результате ряда опытов получают семейство реализаций случайного процесса (Рис.6.2).

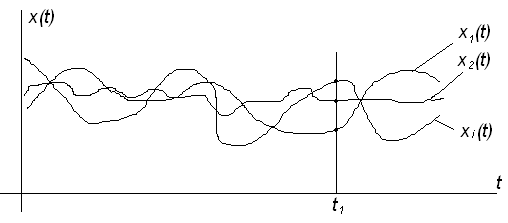
Рисунок 6.2 – Семейство реализаций случайного процесса

В каждом сечении, например, в некоторый фиксированный момент времени случайный процесс представляет собой обыкновенную случайную величину, которая принимает значения .

Поэтому случайный процесс можно трактовать как систему бесчисленного множества случайных величин.

6.2 Закон распределения случайного процесса

Под законом распределения случайного процесса понимают всякое соотношение, устанавливающее связь между реализацией случайного процесса и вероятностью ее появления.

Пусть нас интересует реализация случайного процесса x(t), проходящая через точки (таблица 6.1).

Таблица 6.1

t	t0	t1	t2	…	ti	…	tn
x	x0	x0	x2	…	xi	…	xn

Функция называется n – мерной функцией распределения вероятностей случайного процесса и определяется как вероятность того, что случайный процесс X(t) в моменты времени примет значения меньшие соответственно , т.е.

. (6.1)

Если функция имеет смешанную частную производную по аргументам , т.е.

, (6.2)

то она называется n – мерной плотностью вероятности случайного процесса.

Эти функции в зависимости от числа сечений позволяют получить наиболее полное описание случайного процесса. Однако для решения многих инженерных задач достаточно знать одномерный или двумерный закон распределения случайного процесса, т.е. или . Если эти законы имеют нормальное распределение, то и случайный процесс X(t) также называют нормальным.