
- •§ 2. Характеристики суммы случайных функций
- •§ 3. Характеристики производной от случайной функции
- •§ 4. Характеристики интеграла от случайной функции
- •Тема 2. Каноническое разложение
- •Тема 3. Стационарные случайные процессы § 1. Характеристики стационарной случайной функции
- •§2. Стационарно связанные случайные функции
- •§ 6. Спектральная плотность стационарной случайной функции
- •§ 7. Преобразование стационарной случайной функции стационарной линейной динамической системой
Тема 2. Каноническое разложение
Каноническим разложением случайной функции X(t) называется ее представление в виде
![]() (1)
(1)
где Vk (k=l, ..., m) —центрированные, некоррелированные случайные величины с дисперсиями Dk (k = 1, ..., m); φk (t) (k = 1, ..., m) — неслучайные функции.
Случайные величины Vk (k = it ..., m) называются коэффициентами, а функции φk(t) (k=1, ..., т) —координатными функциями канонического разложения.
Если случайная функция X (t) допускает каноническое разложение (1) в действительной форме, то корреляционная функция Kx(t, t') выражается суммой вида
![]()
которая называется каноническим разложением корреляционной функции.
Задачи
2.1
[9.12] Задана
случайная функция
![]() где V1
и
V2—
некоррелированные случайные величины
с характеристиками
где V1
и
V2—
некоррелированные случайные величины
с характеристиками
![]() .
Найти характеристики случайной функции
X(t).
.
Найти характеристики случайной функции
X(t).
2.2
[9.13] Случайная
функция X
(t)
задана
своим каноническим разложением
![]() где Vi
-
центрированные случайные величины с
дисперсиями
где Vi
-
центрированные случайные величины с
дисперсиями
![]() (i=
1,2,..., n);
М[ViVj]
= 0
при i
(i=
1,2,..., n);
М[ViVj]
= 0
при i![]() j,
a
—неслучайная величина. Найти характеристики
случайной функции X(t).
j,
a
—неслучайная величина. Найти характеристики
случайной функции X(t).
2.3 [9.14] Случайная функция X(t) задана каноническим разложением X(t)=t+V1cosωt+V2sin ωt, где V1 и V2—некоррелированные случайные величины с математическими ожиданиями, равными нулю, и с дисперсиями D1 = D2 = 2. Определить, является ли стационарной случайная функция X(t).
2.4
[9.15] Заданы
две случайные функции: X(t)=t+V1cosωt+
+V2sinωt,
Y(t)=t+U1cosωt+U2sinωt.
Математические ожидания всех случайных
величин V1,
V2,
U1,
U2
равны
нулю, дисперсии равны
![]()
![]() нормированная корреляционная матрица
системы (V1,
V2,
U1,
U2)
имеет
вид:
нормированная корреляционная матрица
системы (V1,
V2,
U1,
U2)
имеет
вид:
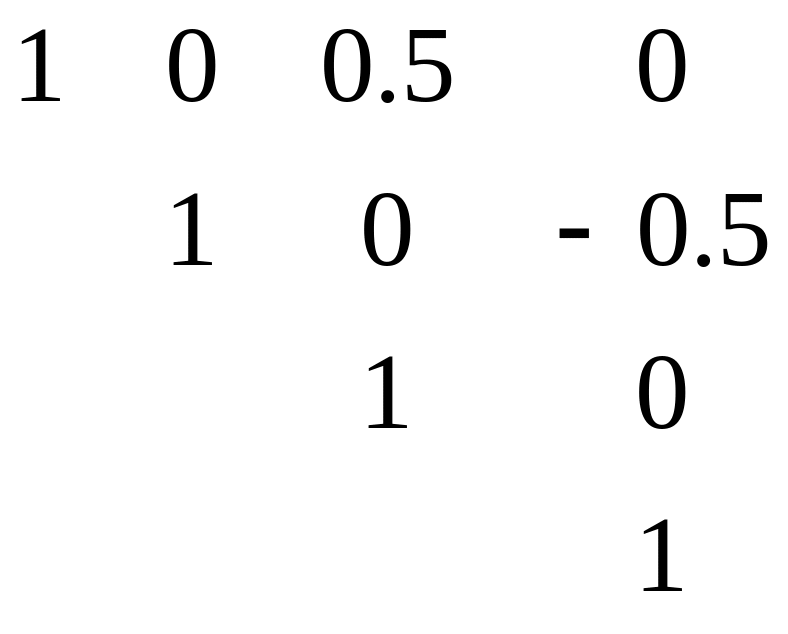
Определить взаимную корреляционную функцию Rxy(t,t’) и найти значение этой функции при t=0, t’=1. Определить Ryx(t,t’) и найти значение этой функции при t=0; t’=1.
2.5
[14.617] Случайный
процесс X(t)
задан
представлением X(t)=
=t+U1cost+U2sint,
где М
[U1]
= 1, M[U2]==2,
![]() Найти канонические разложения процесса
и корреляционной функции.
Найти канонические разложения процесса
и корреляционной функции.
2.6
[14.619] Случайная
функция задана каноническим разложением
X(t)=t+М1cost+М2sint,
D[V1]=1,
D[V2]=2.
Вычислить математическое ожидание,
дисперсию и корреляционную функцию
процесса a)![]() б)
.
б)
.
2.7 [14.621] Случайный процесс X(t) задан каноническим разложением X(t)=1+Ut+Vt2 с характеристиками DU=3, Dv=l. Найти математическое ожидание и корреляционную функцию производной данного процесса. Найти математическое ожидание и дисперсию процесса.
Ответы
2.1
mx(t)=0;Kx(t,t’)=![]()
![]() .
2.2
mx(t)=a;
.
2.2
mx(t)=a;![]()
![]() 2.4
a)
Rxy(t,t’)=cos(ω1t+ω2t’),
Rxy(0,1)=cosω2;
б) Ryx(t,t’)=cos(ω1t’+ω2t),
Ryx(0,1)=cosω1.
2.5
X(t)=t+cost+2sint+V1φ1(t)+V2φ2(t),
Kx(t1,t2)=
=φ1(t1)φ2(t2)+(13/8)
φ2(t1)φ2(t2),
где
φ(t)=Aψ(t), V=(AT)-1
2.4
a)
Rxy(t,t’)=cos(ω1t+ω2t’),
Rxy(0,1)=cosω2;
б) Ryx(t,t’)=cos(ω1t’+ω2t),
Ryx(0,1)=cosω1.
2.5
X(t)=t+cost+2sint+V1φ1(t)+V2φ2(t),
Kx(t1,t2)=
=φ1(t1)φ2(t2)+(13/8)
φ2(t1)φ2(t2),
где
φ(t)=Aψ(t), V=(AT)-1![]() ,
A=
,
A=![]() ,
(AT)-1=
,
(AT)-1=![]() .
2.6
a)
mz(t)=1,
Dz(t)=1+cos2t,
Kz(t1,t2)=sint1sint2+
+2cost1cost2;
б)
my(t)=t2/2,
Dy(t)=(1-cost)2+2(1-cost),
Ky(t1,t2)=sint1sint2+
+2cost1cost2-2(cost1+cost2)+2.
2.7
mz(t)=0,
Kz(t1,t2)=3+4t1t2,
где
Z(t)= =dX(t)/dt.
.
2.6
a)
mz(t)=1,
Dz(t)=1+cos2t,
Kz(t1,t2)=sint1sint2+
+2cost1cost2;
б)
my(t)=t2/2,
Dy(t)=(1-cost)2+2(1-cost),
Ky(t1,t2)=sint1sint2+
+2cost1cost2-2(cost1+cost2)+2.
2.7
mz(t)=0,
Kz(t1,t2)=3+4t1t2,
где
Z(t)= =dX(t)/dt.
Тема 3. Стационарные случайные процессы § 1. Характеристики стационарной случайной функции
Стационарной называют случайную функцию X(t), математическое ожидание которой постоянно при всех значениях аргумента t и корреляционная функция которой зависит только от разности аргументов t2 – t1. Отсюда следует, что:
1. Корреляционная функция стационарной случайной функции есть функция одного аргумента τ= t2 – t1:
Kx(t1, t2)=kx(t2 – t1)=kx(τ).
2. Дисперсия стационарной случайной функции постоянна при вcex значениях аргумента t и равна значению корреляционной функции в начале координат (τ=0):DX(t)=kx(0).
Корреляционная функция стационарной функции обладает следующими свойствами.
Свойство 1. Корреляционная функция стационарной случайной функции —четная функция :kx(τ)=kx(-τ).
Свойство
2. Абсолютная
величина корреляционной функции
стационарной случайной функции не
превышает ее значения в начале координат:
| kx
(τ)
|
![]() kx
(0).
kx
(0).
Нормированной корреляционной функцией стационарной случайной функции называют неслучайную функцию аргумента τ:
ρx(τ)=kx(τ)/kx(0).
Абсолютная величина нормированной коорреляционной функции не превышает единицы: | ρх (τ) |< 1.
Задачи
3.1[14.585] Двумерный
закон распределения случайной функции
X(t)
описывается плотностью
![]() ,
где υ>0.
Найти основные характеристики: mx(t),
Dx(t)
и Kx(t1,
t2).
,
где υ>0.
Найти основные характеристики: mx(t),
Dx(t)
и Kx(t1,
t2).
3.2[14.586]
Случайная величина является частным
случаем такой случайной функции, у
которой отсутствует зависимость от t.
Пусть X(t)=X
для
всех t![]() R,
причем X
— С.В.Н.Т., подчиняющаяся показательному
распределению с параметром λ=
2.
Найти mх
(t),
Dx
(t)
и F2
(x,
у/t1,
t2).
R,
причем X
— С.В.Н.Т., подчиняющаяся показательному
распределению с параметром λ=
2.
Найти mх
(t),
Dx
(t)
и F2
(x,
у/t1,
t2).
3.3[14.587] Случайный процесс Х(t) имеет вид X(t) =Vt2, (t>0), где V—случайная величина, равномерно распределенная на [0,3]. Найти одномерную функцию распределения и одномерную плотность этого процесса.
3.4 [14.588] Случайная функция X(t) задана в виде X(t)=Vt+b, где V—С. В. Н. Т., подчиняющаяся закону N (m, σ), a b—неслучайная константа. Найти одномерную плотность f1(x/t) и основные характеристики процесса: mx(t), σx(t) и Kx(t1, t2).
3.5[14.589] Случайная функция Х(t) задана в виде X(t)=U+Vt, где U и V—независимые случайные величины, подчиняющиеся одному и тому же закону распределения N(m,σ). Используя свойства математического ожидания и дисперсии, вычислить mx(t), Dx(t) и Kx(t1, t2).
3.6[14.591] Заданы плотности fU(u) и fv(v) независимых случайных величин U и V. Записать одномерную плотность f1(x/t) процесса X(t)=U+Vt при t > 0.
3.7[14.592] Заданы корреляционные функции Kx(t1, t2) и Ky(t1, t2) и математические ожидания mx(t) и my(t) двух независимых случайных процессов X(t) и Y(t). Найти корреляционную функцию процесса Z(t)=X(t)Y (t).
3.8[14.593] Показать, что если две случайные функции X(t) и Y (t) некоррелированы при любом фиксированном t и имеют нулевые математические ожидания, то а корреляционная функция их произведения равна произведению корреляционных функций отдельных сомножителей.
3.9 [14.594] Доказать следующее свойство корреляционной функции: если Y(t)=ψ(t)Х(/)+φ(t), где φ(t) и ψ(t) —неслучайные функции, то KY(t1, t2)=ψ(t1)ψ(t2)KX(t1,t2).
3.10
[14.595]
Дана корреляционная функция случайного
процесса X(t):
![]() Найти корреляционную функцию и дисперсию
процесса
Найти корреляционную функцию и дисперсию
процесса
![]()
3.11 [14.596] Случайный процесс Z(t) задан в виде Z(t)=X(t)+ +tY(t)+t2, где X(t) и Y (t) — некоррелированные случайные процессы с
характеристиками
![]()
![]()
Найти mz(t) и Dz(t).
3.12[14.598] Заданы случайные функции Х(t) = -Usint + Vcost, Y(t)=Ucost + Vsint, где U и V—некоррелированные стандартизованные случайные величины. Найти автокорреляционные функции ρx(t1, t2) и ρy(t1, t2) процессов Х(t) и Y(t), а также корреляционную функцию связи ρxy(t1, t2).
3.13 [830] Задана случайная функция X(t)=cos(t+φ), где φ—случайная величина, распределенная равномерно в интервале (0,2 π). Доказать, что X(t)—стационарная функция.
3.14[831] Задана случайная функция X(t)=sin(t + φ), где φ—случайная величина, распределенная равномерно в интервале (0, 2π). Доказать, что X (t)—стационарная функция.
3.15[832] Доказать, что если X(t)—стационарная случайная функция, Y—случайная величина, не связаннаяс Х(t) то случайная функция Z(t)=X(t) + Y стационарна.
3.16 [833] Доказать, что если X(t)—стационарная случайная функция, Y=Х(t0) —случайная величина, то случайная функция Z(t) = X(t) + Y нестационарна.
3.17[834] Стационарна ли случайная функция X (t) = Ucos2t, где U—случайная величина?
3.18[835] Является ли стационарной случайная функция X(t)=Usint +Vcost, где U и V—некоррелированные случайные величины, причем mu=mv= 0, Du=Dv=D?
3.19[836]
Задана
случайная функция X
(t)
= t2
+ Usint
+ Vcost,
где U
и V—случайные
величины, причем M(U)=M(V)=0,
М(UV)=0;
D(U)=D(V)=10.
Доказать, что: а) Х(t)
— нестационарная функция; б)
![]() (t)
—стационарная функция.
(t)
—стационарная функция.
3.20[837] Будет ли стационарной случайная функция X(t)=asin(ωt+φ), где а, ω—положительные постоянные числа: φ—случайная величина, плотность распределения которой f(φ) = cosφ в интервале (0, π/2)?
3.21[838]
Доказать нестационарность случайной
функции X(t)=
=asin(ωt+φ),
где а,
ω—положительные
числа; φ—нормально
распределенная случайная величина,
плотность вероятности которой f(φ)
= (1/![]() )
)![]()
3.22 [839] Найти дисперсию случайной функции X(t)= asin(ωt+ φ), где а, ω—положительные числа; φ—нормально распределенная случайная величина, плотность вероятности которой f(φ) = (1/ )
3.23 [840] Доказать, что корреляционная функция стационарной случайной функции есть четная функция.
3.24 [841] Известна корреляционная функция kx(τ) стационарной функции X(t). Доказать, что если Y(t) = aX(t), то ky(τ)=a2kx(τ).
3.25[842]
Известна
корреляционная функция
![]() стационарной случайной функции X(t).
Найти корреляционную функцию случайной
функции Y(t)
= 4X(t).
стационарной случайной функции X(t).
Найти корреляционную функцию случайной
функции Y(t)
= 4X(t).
3.26[843] Доказать, что дисперсия стационарной случайной функции X(t) постоянна и равна значению корреляционной функции в начале координат: Dx(t) = kx(0).
3.27 [844] Доказать, что абсолютная величина корреляционной функции стационарной случайной функции не превышает ее значения вначале координат: |kx(τ)] kx(0).
3.28
[845] Найти
нормированную корреляционную функцию,
зная корреляционную функцию стационарной
случайной функции X(t):
а) kx(τ)
= 3![]() ;
б) kx(τ)=Dxe-|τ|·(1+|τ|).
;
б) kx(τ)=Dxe-|τ|·(1+|τ|).
Ответы
3.1
mx(t)=υt,
Dx(t)=1+t2,
Kx(t1,t2)=![]() 3.2
mx(t)=1/2;
Dx(t)=1/4;
F2(x,y/t1,t2)=
3.2
mx(t)=1/2;
Dx(t)=1/4;
F2(x,y/t1,t2)=![]() 3.3
F1(x/t)=
3.3
F1(x/t)=![]() f1(x/t)=
f1(x/t)=![]() 3.4
3.4
![]() mx(t)=tm+b,
σx(t)=σ|t|,
Kx(t1,t2)=t1t2σ2.
3.5
mx(t)=m(1+t),
Dx(t)=σ2(1+t2),
Kx(t1,t2)=σ2(1+t1t2).
3.6
f1(x/t)=
mx(t)=tm+b,
σx(t)=σ|t|,
Kx(t1,t2)=t1t2σ2.
3.5
mx(t)=m(1+t),
Dx(t)=σ2(1+t2),
Kx(t1,t2)=σ2(1+t1t2).
3.6
f1(x/t)=![]() t>0.
3.7
Kz(t1,t2)=Kx(t1,t2)
Ky(t1,t2)+
Kx(t1,t2)my(t1)my(t2)+
Ky(t1,t2)mx(t1)mx(t2).
3.10
Ky(t1,t2)=
t>0.
3.7
Kz(t1,t2)=Kx(t1,t2)
Ky(t1,t2)+
Kx(t1,t2)my(t1)my(t2)+
Ky(t1,t2)mx(t1)mx(t2).
3.10
Ky(t1,t2)=
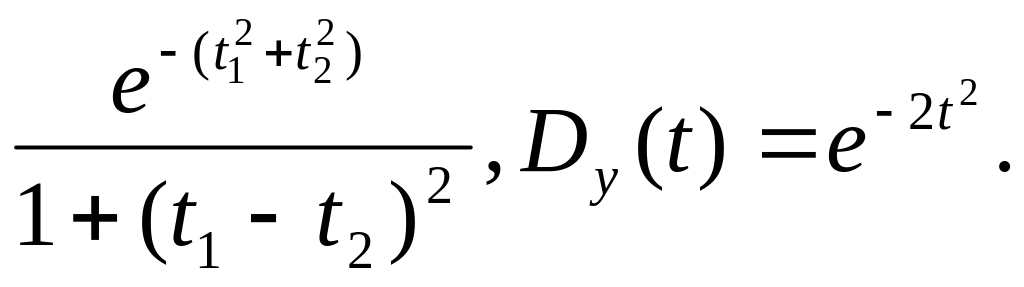 3.11
mz(t)=4+t+t2,
Dz(t)=9+4t2.
3.12
ρx(t1,t2)=ρy(t1,t2)=cos(t2-t1),
ρxy(t1,t2)=sin(t2-t1).
3.14
mx(t)=0,
Kx(t)=
=(1/2)cos(t2-t1).
3.17
X(t)
– нестационарная
функция:
mx(t)=mucos2t
≠ const. 3.18
X(t)
– стационарная
функция:
mx(t)=0;
Kx(t)=Dcos(t2-t1).
3.20
X(t)
– нестационарная
функция:
mx(t)=
3.11
mz(t)=4+t+t2,
Dz(t)=9+4t2.
3.12
ρx(t1,t2)=ρy(t1,t2)=cos(t2-t1),
ρxy(t1,t2)=sin(t2-t1).
3.14
mx(t)=0,
Kx(t)=
=(1/2)cos(t2-t1).
3.17
X(t)
– нестационарная
функция:
mx(t)=mucos2t
≠ const. 3.18
X(t)
– стационарная
функция:
mx(t)=0;
Kx(t)=Dcos(t2-t1).
3.20
X(t)
– нестационарная
функция:
mx(t)=![]() .
3.22
Dx(t)=a2[0.5-(1/2e2)2]cos2ωt+a2[0.5-(1/e)-(1/2e2)]sin2ωt.
.
3.22
Dx(t)=a2[0.5-(1/2e2)2]cos2ωt+a2[0.5-(1/e)-(1/2e2)]sin2ωt.
3.25
![]() 3.28
a)
ρx(τ)=
;
б)
ρx(τ)=e-|τ|(1+|τ|).
3.28
a)
ρx(τ)=
;
б)
ρx(τ)=e-|τ|(1+|τ|).
