Тема 1. Основные понятия.

§1. Основные понятия. Характеристики случайных функций

Задачи

Ответы

§ 2. Характеристики суммы случайных функций

Задачи

Ответы

§ 3. Характеристики производной от случайной функции

Задачи

Ответы

§ 4. Характеристики интеграла от случайной функции

Задачи

Ответы

Тема 2. Каноническое разложение

Задачи

Ответы

Тема 3. Стационарные случайные процессы

§ 1. Характеристики стационарной случайной функции

Задачи

Ответы

§2. Стационарно связанные случайные функции

Задачи

Ответы

§ 3. Корреляционная функция производной от стационарной случайной функции

Задачи

Ответы

§ 4. Корреляционная функция интеграла от стационарной случайной

функции

Задачи

Ответы

§ 5. Взаимная корреляционная функция дифференцируемой стационарной случайной функции и ее производных

Задачи

Ответы

§ 6. Спектральная плотность стационарнойслучайной функции

Задачи

Ответы

§ 7. Преобразование стационарной случайной функции стационарной линейной динамической системой

Задачи

Ответы

Тема 1. Основные понятия.

Характеристики случайных функций

§1. Основные понятия. Характеристики случайных функций

Случайной функцией X (t) называют функцию неслучайного аргумента t, которая при каждом фиксированном значении аргумента является случайной величиной.

Сечением случайной функции X(t) называют случайную величину, соответствующую фиксированному значению аргумента случайной функции.

Реализацией случайной функции X(t) называют неслучайную функцию аргумента t, которой может оказаться равной случайная функция в результате испытания.

Таким образом, случайную функцию можно рассматривать как совокупность случайных величин {X (t)}, зависящих от параметра t, или как совокупность ее возможных реализаций.

Характеристиками случайной функции называют ее моменты, которые являются неслучайными функциями.

Математическим ожиданием случайной функции X (t) называют неслучайную функцию m_x(t), значение которой при каждом фиксированном значении аргумента равно математическому ожиданию сечения, соответствующего этому же фиксированному значению аргумента:

m_x(t)=M[X(t)].

Свойства математического ожидания случайной функции.

Свойство 1. Математическое ожидание неслучайной функции φ(t) равно самой неслучайной функции:

M[φ(t)]= φ(t).

Свойство 2. Неслучайный множитель φ(t) можно выносить за знак математического ожидания:

M[φ(t)·X[t]]= φ(t)·M[X(t)]=φ(t)·m_x(t).

Свойство 3. Математическое ожидание суммы двух случайных функций равно сумме математических ожиданий слагаемых:

М [X (t)+Y (t)] =т_х (t)+m_y (t).

Свойство можно обобщить на п слагаемых функций:

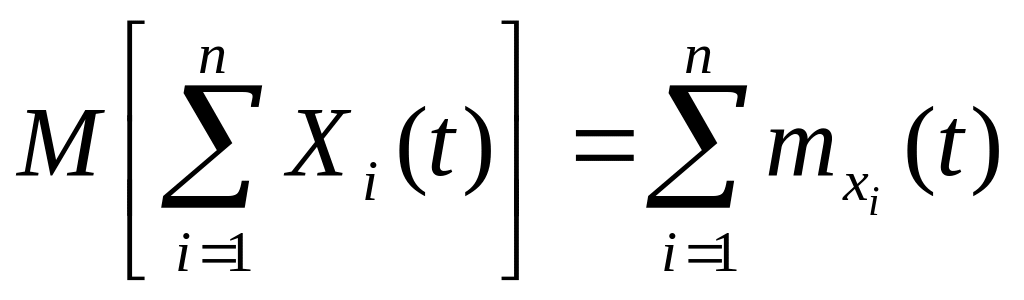
Следствие. Если X(t) —случайная функция, φ(t)—неслучайная функция, то

М [X (t)+φ (t)] =т_х (t)+φ (t).

Дисперсией случайной функции X(t) называют неслучайную неотрицательную функцию D_x (t), значение которой при каждом фиксированном значении аргумента t равно дисперсии сечения, соответствующего этому же фиксированному значению аргумента:

D_x(t)=D[X(t)].

Средним квадратическим отклонением случайной функции называют квадратный корень из дисперсии:

Свойства дисперсии случайной функции.

Свойство 1. Дисперсия неслучайной функции φ(t) равна нулю:

D [φ(t)]=0.

Свойство 2. Дисперсия суммы случайной функции X (t) и неслучайной функции φ(t) равна дисперсии случайной функции:

D [X(t)+φ(t))=D_x(t).

Свойство 3. Дисперсия произведения случайной функции X(t) на неслучайную функцию φ(t) равна произведению квадрата неслучайного множителя на дисперсию случайной функции:

D[X(t)·φ(t)]=φ²(t)·D_x(t).

Центрированной случайной функцией называют разность между случайной функцией и ее математическим ожиданием:

Корреляционной функцией случайной функции X(t) называют неслучайную функцию К_х (t₁, t₂) двух независимых аргументов t₁ и t₂ значение которой при каждой паре фиксированных значений аргументов равно корреляционному моменту сечений, соответствующих этим же фиксированным значениям аргументов:

При равных между собой значениях аргументов t₁=t₂=t корреляционная функция случайной функции равна дисперсии этой функции:

K_x(t, t)=D_x(t).

Свойства корреляционной функции.

Свойство 1. При перестановке аргументов корреляционная функция не изменяется (свойство симметрии):

K_x(t₁, t₂)= K_x(t₂, t₁).

Свойство 2. Прибавление к случайной функции X(t) неслучайного слагаемого φ(t) не изменяет ее корреляционной функции: если Y(t)=X(t)+φ(t), то

K_y(t₁, t₂)= K_x(t₁, t₂).

Свойство 3. При умножении случайной функции X (t) на неслучайный множитель φ(t) ее корреляционная функция умножается на произведение φ(t₁)·φ(t₂): если Y(t)=X(t)·φ(t),то

K_y(t₁, t₂)=K_x(t₁, t₂)· φ(t₁)·φ(t₂).

Свойство 4. Абсолютная величина корреляционной функции не превышает среднего геометрического дисперсий соответствующих сечений:

Нормированной корреляционной функцией случайной величины X(t) называют неслучайную функцию двух независимых переменных t₁ и t₂ , значение которой при каждой паре фиксированных значений аргументов равно коэффициенту корреляции сечений, соответствующих этим же фиксированным значениям аргументов:

Абсолютная величина нормированной корреляционной функции не привышает единицы:

Взаимной корреляционной функцией двух случайных функций X(t) и Y(t) называют неслучайную функцию R_xy(t₁, t₂) двух независимых аргументов t₁ и t₂, значение которой при каждой паре фиксированных значений аргументов равно корреляционному моменту сечений обеих функций, соответствующих этим же фиксированным значениям аргументов:

Коррелированными называют две случайные функции, если их взаимная корреляционная функция не равна тождественно нулю.

Некоррелированными называют две случайные функции, взаимная корреляционная функция которых тождественно равна нулю.

Свойства взаимной корреляционной функции.

Свойство 1. При одновременной перестановке индексов и аргументов корреляционная функция не изменяется:

R_xy(t₁, t₂)=R_yx(t₂, t₁).

Свойство 2. Прибавление к случайным функциям X(t) и Y(t) неслучайных слагаемых φ(t) и ψ(t) не изменяет их взаимной корреляционной функции: если

X₁(t)=X(t)+φ(t), Y₁(t)=Y(t)+ψ(t),

то

Свойство 3. При умножении случайных функций X(t) и Y(t) на неслучайные множители, соответственно φ(t) и ψ(t), взаимная корреляционная функция умножается на произведение φ(t₁)·ψ(t₂):

если

X₁(t)=X(t)·φ(t), Y₁(t)=Y(t)·ψ(t),

то

Свойство 4. Абсолютная величина взаимной корреляционной функции двух случайных функций X(t) и Y(t) не превышает среднего геометрического их дисперсий:

Нормированной взаимной корреляционной функцией двух случайных функций X(t) и Y(t) называют неслучайную функцию двух независимых аргументов t₁ и t₂:

Абсолютная величина нормированной взаимной корреляционной функции не превышает единицы:

Задачи

1.1 [9.1] Случайная функция X (t) в каждом сечении представляет собой непрерывную случайную величину с плотностью распределения f(x,t). Написать выражения для математического ожидания т_х (t) и дисперсии D_x (t) случайной функции X(t).

1.2 [9.2] Случайная функция X(t) представляет собой случайную величину X(t) = V, где V — непрерывная случайная величина с плотностью распределения φ(υ). а) Написать выражение одномерного закона (плотности) распределения f(x,t) случайной функции X(t). б) Найти математическое ожидание m_x(t) и дисперсию D_x(t) случайной функции X(t). в) Написать выражение двумерной функции распределения F(x₁, x₂, t₁, t₂) двух сечений X(t₁), X(t₂) случайной функции X(t).

1.3 [9.3] Случайная функция X(t) задана в виде X(t)=Vt+b, где V—случайная величина, распределенная по нормальному закону с параметрами m_υ, σ_υ, b - не случайная величина. Найти плотность распределения f(x,t) сечения случайной функции X(t) и ее характеристики m_x(t), D_x(f), K_x(t, t').

1.4 [9.4] Показать, что любая функция двух аргументов вида

где D_i – неотрицательные числа, φ_i(t) — любые действительные функции (i=1, ...,n), обладает всеми свойствами корреляционной функции.

1.5 [766] Доказать, что при умножении случайной функции X(t) на неслучайный множитель φ(t) корреляционная функция умножается на произведение φ(t₁)·φ(t₂).

1.6 [767] Известна корреляционная функция К_x случайной функции X(t). Найти корреляционную функцию случайной функции: a) Y(t)=X(t)·(t+1); б) Z(t) = CX(t),где С — постоянная.

1.7 [768] Пусть X(t)—случайная функция, φ(t)—неслучайная функция. Доказать: если Y(t)=X(t)+φ(t), то D_y(t) = D_x(t).

1.8 [769] Известна дисперсия D_x(t) случайной функции X(t). Найти дисперсию случайной функции Y(t) =Х(t)+2.

1.9 [770] Дано: X (t) — случайная функция, φ(t) — неслучайная функция. Доказать: если Y (t) = Х(t)·φ(t), то D_y(t)=φ²(t)·D_x(t).

1.10 [771] Известна дисперсия случайной функции X(t). Найти дисперсию случайной функции Y (t) = (t + 3) X (t).

1.11 [772] На вход усилительного звена подается случайная функция Х(t), математическое ожидание и корреляционная функция которой известны: m_x(t)=t, . Найти: а) математическое ожидание; б) корреляционную функцию выходной случайной функции Y(t), если коэффициент усиления k = 5.

1.12 [773] Доказать, что корреляционная функция произведения двух центрированных некоррелированных случайных функций равна произведению корреляционных функций сомножителей.

1.13 [774] Доказать, что корреляционная функция произведения трех центрированных независимых случайных функций равна произведению корреляционных функций сомножителей.

1.14 [775] Найти: а) математическое ожидание; б) корреляционную функцию; в) дисперсию случайной функции X(t) = Ucos2t, где U—случайная величина, причем M(U) = 5, D(U) = 6.

1.15 [776] Найти: а) математическое ожидание; б) корреляционную функцию; в) дисперсию случайной функции X(t) = sin3t, где U—случайная величина, причем М(U)=10, D(U) = 0,2.

1.16 [777] Известна корреляционная функция случайной функции Х(t). а) Убедиться на примере при t₁=1, t₂=2 что абсолютная величина корреляционной функции не превышает среднего геометрического дисперсий соответствующих сечений; б) найти нормированную корреляционную функцию и вычислить коэффициент корреляции сечений, соответствующих значениям аргументов t₁=1, t₂=4.

1.17 [778] Задана корреляционная функция случайной функции X(t). Найти нормированную корреляционную функцию.

1.18 [779] Найти взаимную корреляционную функцию двух случайных функций: X(t)=t²U и Y(t)=t²U, где U —случайная величина, причём D(U) = 5.

1.19 [780] Доказать, что взаимная корреляционная функция случайных функций Х(t) и Y(t) равна взаимной корреляционной функции центрированных функций и

1.20 [781] Доказать, что при одновременной перестановке индексов и аргументов взаимная корреляционная функция двух случайных функций не изменяется: R_xy(t₁, t₂)=R_yx(t₂,t₁).

1.21 [782] Задана взаимная корреляционная функция R_xy(t₁, t₂)= = cos(αt₁+βt₂). Написать взаимную корреляционную функцию R_yx(t₁,t₂).

1.22 [783] Найти нормированную взаимную корреляционную функцию случайных функций X(t)=tU и Y(t)=(t+l)U, где U—случайная величина, причем дисперсия D (U)=10.

Ответы

1.1 . 1.2 a) f(x,t)=φ(x); б) ,

1.3 f(x,t)- нормальный закон с параметрами m_υt+b, |t|σ_υ; m_x(t)=m_υt+b; ; ;

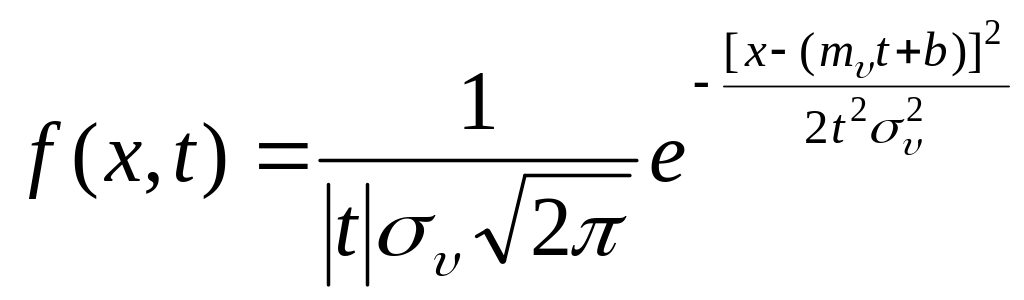
1.4 Достаточно показать, что существует случайная функция X(t), имеющая корреляционную функцию 1.6 а) K_y=(t₁+1)(t₂+1)K_x; б) K_z=C²K_x 1.8 D_y(t)=D_x(t) 1.10 D_y(t)=(t+3)²D_x(t). 1.11 a) m_y(t)=5t, . 1.14 a) M[X(t)]=5cos2t; б) K_x(t₁, t₂)=6 cos2t₁ cos2t₂; в) D_x(t)=6 cos²2t. 1.15 a) m_x(t)=10sin3t; б) K_x=0,2sin 3t₁ sin 3t₂; в) D_x(t)=0,2sin²3t. 1.16 а) K_x(1,2)=22, D_x(1)=6, D_x(2)=84; б) . 1.17 , если аргументы одного знака, , если аргументы разных знаков. 1.18 R_xy=5 . 1.21 R_yx(t₁,t₂)= R_xy(t₂,t₁)=cos(αt₂+βt₁). 1.22 ρ_xy=1, если t₁ и t₂+1 одного знака; ρ_xy= -1, если t₁ и t₂+1 разных знаков.

§ 2. Характеристики суммы случайных функций

Теорема 1. Математическое ожидание суммы конечного числа случайных функций равно сумме математических ожиданий слагаемых.

Следствие. Математическое ожидание суммы случайной функции и случайной величины равно сумме их математических ожиданий.

Теорема 2. Корреляционная функция суммы двух коррелированных случайных функций равна сумме корреляционных функций слагаемых и взаимной корреляционной функции, которая прибавляется дважды (с разным порядком следования аргументов): если Z(t) = X(t) + Y(t), то

K_z(t₁,t₂) = K_x(t₁,t₂)+ K_y(t₁,t₂)+ R_xy(t₁,t₂)+ R_xy(t₂,t₁).

Теорема обобщается на n попарно коррелированных функций:

если , то

где пары индексов (i, j) второго слагаемого есть размещения из чисел 1, 2, ... n, взятых по два.

Следствие 1. Корреляционная функция суммы некоррелированных случайных функций равна сумме корреляционных функций слагаемых.

Следствие 2. Корреляционная функция случайной функции и некоррелированной с ней случайной величины равна сумме корре­ляционной функции случайной функции и дисперсии случайной величины.

Задачи

1.23 [784] Заданы корреляционные и взаимные корреляционные функции случайных функций X(t) и Y(t). Найти корреляционную функцию случайной функции Z(t)=X(t)+Y(t), если рассматриваемые функции: а) коррелированны; б)не коррелированны.

1.24 [785] Известны математические ожидания m_x(t)=2t+1, m_y(t)=t—1 и корреляционные функции K_x=t₁t₂, некоррелированных случайных функций X(t) и Y(t). Найти: а) математическое ожидание; б) кор­реляционную функцию случайной функции Z(t) = X(t) +Y(t).

1.25 [786] Заданы корреляционные и взаимные корреляционные функции случайных функций X (t) и Y (t). Найти взаимную корреляционную функцию случайных функций U(t) = aX(t)+by(t) и V(t)= cX(t) + dY (t), где а, b, с, d — постоянные действительные числа.

1.26 [787] Заданы корреляционные и взаимные корреляционные функции случайных функций X(t), Y(t), Z(t). Найти корреляционную функцию случайной функции U(t)=X(t)+Y(t)+Z(t), если рассматриваемые функции: a) попарно коррелированны; б) попарно не коррелированны.

1.27 [788] Доказать, что формулу для отыскания корреляционной функции суммы n коррелированных случайных функций можно записать в виде

1.28 [789] Найти математическое ожидание, корреляцион­ную функцию и дисперсию случайной функции Х(t)=Ut+Vt², где U и V—некоррелированные случайные величины, причем M(U) = 4, M(V) = 7, D(U)=0,l, D(V) = 2.

Указание. Принять во внимание, что величины U и V не коррелированны, поэтому их корреляционный момент М [U—m_u) (V—m_υ)]=0.

1.29 [790] Найти математическое ожидание, корреляционную функцию и дисперсию случайной функции X(t) =Usint+Vcost, где U и V—некоррелированные случайные величины, причем М(U)=1, М(V)=8, D(U)=D(V)=4.

1.30 [791] Найти математическое ожидание, корреляционную функцию и дисперсию случайной функции X(t) == Ucos2t+Vsint+t, где U и V—некоррелированные случайные величины, причем M(U)=1, M(V)=2, D(U)=3, D(V) = 4.

Указание. Прибавление к случайной функции неслучайного слагаемого t не изменяет ее корреляционной функции, поэтому достаточно найти корреляционную функцию случайной функции Y(t)=Ucos 2t + Vsint.

1.31 [792] Заданы случайные функции X(t)=Ucost+Vsint, Y(t)=Ucos3t+Vsin3t, где U и V—некоррелированные случайные величины, причем М(U)=М(V)=0, D(U)=D(V)=5. Найти нормированную взаимную корреляционную функцию р_ху(t₁, t₂).

1.32 [793] Найти корреляционную функцию случайной функции X(t)=U₁cosω₁t+V₁sinω₁t+U₂cosω₂t+V₂sinω₂t, где ω₁, ω₂ —постоянные числа; U₁, U₂, V₁, V₂—попарно некоррелированные случайные величины, причем их математические ожидания равны нулю, дисперсии величин U₁ и V₁ равны D₁, дисперсии величин U₂ и V₂ равны D₂.

Ответы

1.23 a) K_Z(t₁, t₂)= K_X(t₁, t₂)+ K_Y(t₁, t₂)+ R_XY(t₁, t₂)+ R_YX(t₂, t₁); б) K_Z= K_X+K_Y. 1.24 a) m_z(t)=3t; 1.26 a) K_V=K_X+K_Y+K_Z+R_XY+R_YX+ +R_XZ+R_ZX+R_YZ+K_ZY; б) K_V =K_X+K_Y+K_Z. 1.28. m_x(t)=4t+7t²; K_x=0.1t₁t₂+ +2 D_x(t)=0.1t²+2t⁴. 1.29 m_x(t)=sint+8cost; K_x=4cos(t₂-t₁); D_x(t)=4. 1.30 m_x(t)=cos2t+2sint+t; K_x=3cos2t₁cos2t₂+4sint₁sint₂; D_x(t)=3cos²2t+4sin²t. 1.31 ρ_xy=cos(3t₂-t₁). 1.32 K_x=D₁cosω₁(t₂-t₁)+D₂cosω₂(t₂-t₁).