§ 4. Характеристики интеграла от случайной функции

Интегралом от случайной функции X (t) пo отрезку [0, t] называют предел в среднеквадратичном интегральной суммы при стремлении к нулю частичного интервала Δs_i максимальной длины (переменная интегрирования обозначена через s, чтобы отличить ее от предела интегрирования t):

Теорема 1. Математическое ожидание интеграла от случайной функции равно интегралу от ее математического ожидания:

если , то

Теорема 2. Корреляционная функция интеграла от случайной функции равна двойному интегралу от ее корреляционной функции:

если , то

Теорема 3. Взаимная корреляционная функция случайной функции X(t) и интеграла равна интегралу от корреляционной функции случайной функции X(t):

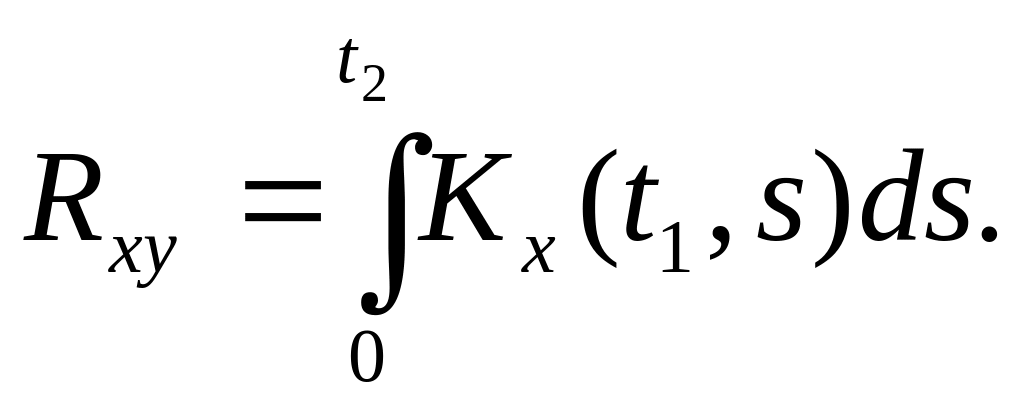
Задачи

1.49 [811] Зная математическое ожидание m_x(t) = 3t² + l случайной функции X (t), найти математическое ожида­ние интеграла .

1.50 [812] Найти математическое ожидание интеграла , зная математическое ожидание случай­ной функции X(t): a) m_x(t)=cost; б) m_x(t)=4cos²t; в) m_x(t)=t—cos2t.

1.51 [813] Задана случайная функция X(t)=Ue^αtcosβt, где U—случайная величина, причем M(U) = 5. Найти математическое ожидание

интеграла .

1.52 [814] Найти математическое ожидание случайной функции , зная случайную функцию X (t): а) X(t)=Ue^αtsint; б) X(t)=Usin²t, где U—случайная величина, причем M(U)=2.

1.53 [815] Задана случайная функция Х(t)=Uсоs²t, где U—случайная величина, причем M(U)=2. Найти математическое ожидание случайной функции

1.54 [816] Задана корреляционная функция K_x(t₁,t₂)=cosωt₁cosωt₂ случайной функции X(t). Найти: а) кор­реляционную функцию; б) дисперсию интеграла .

1.55 [817] Задана корреляционная функция K_x=cosωt₁cosωt₂, случайной функции X(t). Найти: а) корреляционную функцию; б) дисперсию интеграла .

1.56 [818] На вход интегрирующего устройства поступает случайная функция X(t), корреляционная функция которой K_x=t₁t₂. Найти дисперсию на выходе интегратора.

1.57 [819] Найти дисперсию интеграла , зная корреляционную функцию случайной функции X (t):

1.58 [820] На вход интегрирующего устройства поступает случайная функция X(t). Математическое ожидание и корреляционная функция этой случайной функции известны: m_x(t)=cos²t, K_x=cosωt₁cosωt₂. Найти: а) математическое ожидание; б) корреляционную функцию; в) дисперсию на выходе интегратора.

1.59 [821] Задана случайная функция X(t)=Ue^3tcos2t, где U—случайная величина, причем М(U)=5, D(U)=1. Найти: а) математическое ожидание, б) корреляционную функцию; в) дисперсию интеграла .

1.60 [822] Найти дисперсию интеграла , зная случайную функцию: a) X(t) = Ucos2t, где U — случайная величина, причем M(U) = 5, D(U) = 6; б) X(t) =Usint, причем M(U) = 2, D(U)=3.

1.61 [823] Задана корреляционная функция Найти корреляционную функцию случайной функции

1.62 [824] Задана случайная функция X(t)=Ucos3t, где U—случайная величина, причем M(U)=1, D(U)=1. Найти: а) математическое ожидание; б) корреляционную функцию; в) дисперсию случайной функции

1.63 [825] Задана корреляционная функция Найти дисперсию случайной функции

1.64 [826] Задана корреляционная функция . Найти: а) корреляционную функцию; б) дисперсию интеграла .

1.65 [827] Заданы математическое ожидание m_x(t)=3+4t, корреляционная функция . Найти: а) математическое ожидание; б) дисперсию интеграла .

1.66 [828] Доказать, что если известна корреляционная, функция случайной функции Х(t), то взаимные корреляционные функции случайных функций X(t) и выражаются интегралами:

a) 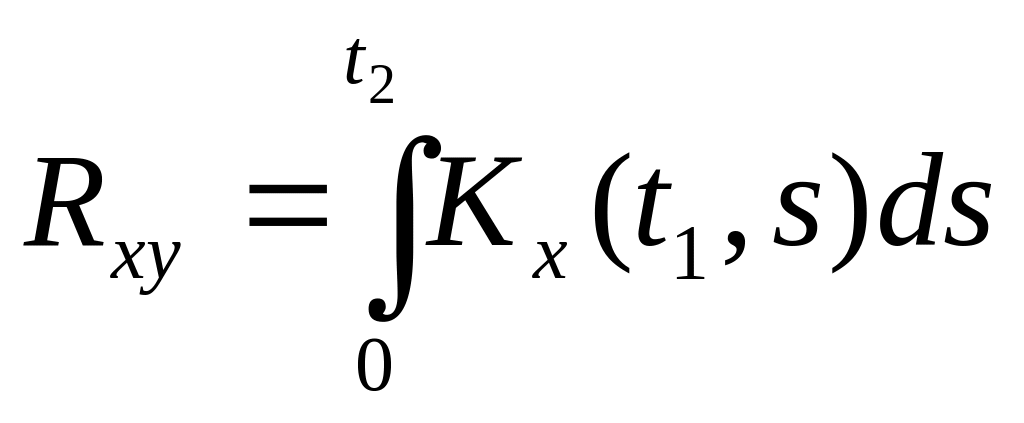; 6) .

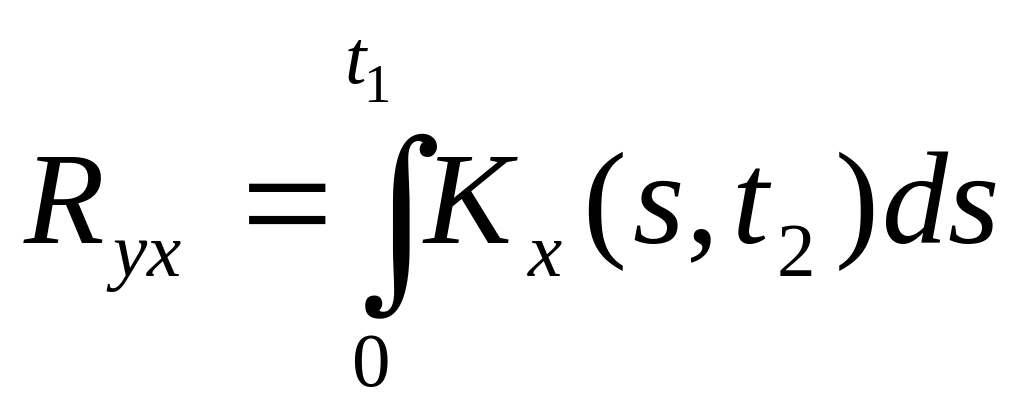1.67 [829] Найти взаимные корреляционные функции случайных функций X(t) и , если известна корреляционная функция K_x случайной функции X(t): a)K_x=2t₁t₂+1; б) K_x=cos t₁ cost₂; в)

Ответы

1.49 m_x(t)=t³+t. 1.50 a) m_y(t)=sint, б) m_y(t)=2t+sin2t, в) m_y(t)=0.5(t²-sin2t). 1.51 m_y(t)=[5/(α²+β²)][e^αt(βsinβt+αcosβt)-α]. 1.52 a) m_y(t)=2/(1+α²) [e^αt(αsint-cost)+1], б) m_y(t)=t-0.5sin2t. 1.53 m_y(t)=(t²+1)(t+0.5sin2t). 1.54 a) K_y(t₁,t₂)=(sinωt₁sinωt₂)/ω²; б) D_y(t)=sin²ωt/ω². 1.55 a) K_y=(cosωt₁-1)(cosωt₂-1)/ω²; б) D_y(t)=(cosωt-1)²/ω². 1.56 D_y(t)=t⁴/4. 1.57 a) D_y(t)= =t⁴[2t²/9)+(3/4)]; б) D_y(t)=[e^t(t-1)+1]²; в) D_y(t)=2t arctgt-ln(1+t²); г) D_y(t)=(1/169)[2e^3tsin2t+3(2e^3tcos2t-1)]. 1.58 a) m_y(t)=0.5[t+(sin2t/2)]; б) K_y=(sinωt₁sinωt₂)/ω²; в) D_y(t)=(sin²ωt)/ω². 1.59 a) m_y(t)=(5/13)[e^3t (2sin2t+3cos2t)-3]; б) K_y(t₁,t₂)=(1/169)[e^3t(2sin2t₁ + 3cos2t₁)-3][e^3t (2sin2t₂+3cos2t₂)-3]; в) D_y(t)= (1/169)[e^3t(2sin2t + 3cos2t)² 1.60 a) D_y(t)= =1.5sin²2t; б) D_y(t)=3(1-cost)². 1.61 1.62 a) m_y(t)= =(sin3t)/3t; б) K_y=(sin3t₁sin3t₂)/9 t₁t₂; в) D_y(t)=(sin²3t)/9t². 1.63 D_y(t)= =e^2αt(βsinβt+αcosβt-α)²/4t⁴(α²+β²)².

1.64 a) где min(t₁,t₂)- наименьшее из чисел t₁ и t₂; б) D_y(t)=2D(t+e^-t-1). 1.65 a) m_y(t)=3t+2t²; б) D_y(t)=5(2t+e^-2t-1). 1.67 a) R_xy=t₁ +t₂; б) R_xy=sint₂cost₁; в) R_xy=t₁ [(t₂-1) +1], R_yx=t₂ [(t₁-1) +1].