3. Статистические свойства выборочных главных компонент; статистическая проверка некоторых гипотез

Смысл математико-статистических методов, как известно, состоит в том, чтобы по некоторой части исследуемой генеральной совокупности (т. е. по выборке, или, что то же, — по ограниченному ряду наблюде­ний X₁, Х₂, ..., Х_n ) выносить обоснованные суждения о ее свойствах в целом.

Применительно к нашей задаче нас, в первую очередь, будет инте­ресовать, как сильно свойства и характеристики выборочных главных компонент могут отличаться от соответствующих свойств и характери­стик главных компонент всей генеральной совокупности, и, в частности,. как эта мера отличия зависит от объема выборочной совокупности (n), но которой эти выборочные главные компоненты были построены. Так, например, для изучения природы внутренних связей между характе­ристиками различных статей семейного бюджета потребления и для выявления небольшого числа наиболее существенных в этом смысле показателей исследователь может обследовать какое-то количество (n) семей и по полученным результатам наблюдения X₁, Х₂, ..., Х_n по­строить главные компоненты . Однако, увеличивая объем выборки п, т.е. добавляя к нашим наблюдениям результаты на­блюдения по дополнительно обследованным семьям, естественно ожи­дать, что пересчет главных компонент с учетом добавленных наблюде­ний, вообще говоря, изменит (хотя, быть может, и незначительно) ра­нее полученные значения интересующих нас характеристик: (i = 1. 2, .... р) и т.п. В то же время существует, по-видимому, такое (столь большое) n, дальнейшее увеличение которого уже не будет прак­тически приводить к изменению основных характеристик главных ком­понент (другими словами, мы вправе ожидать, что главные компоненты выборок достаточно большого объема практически совпадают с глав­ными компонентами всей генеральной совокупности).

Выяснению некоторых вопросов, связанных с. оценкой близости различных выборочных () и теоретических () ха­рактеристик главных компонент, и посвящен настоящий пункт. При этом, приведенные ниже результаты исследований неизменно опирают­ся на допущение нормальности исследуемой генеральной совокупности и взаимной независимости извлеченных из нее наблюдений. Как и преж­де под X₁, Х₂, ..., Х_n мы будем понимать центрированные наблюдения, которые, строго говоря, даже при независимых исходных наблюдениях уже не будут независимыми. Однако при достаточно больших п мы мо­жем пренебречь этим эффектом нарушения независимости. Таким обра­зом, X_i N (, ), i = 1,2, ..., п (как следует из предыдущего, вектор средних значений а = М Х определяет лишь точку в р-мерном прост­ранстве, в которую переносится начало координат при переходе к глав­ным компонентам, и мы с самого начала будем считать этот перенос уже осуществленным).

а) Вспомогательные факты, относящиеся к свойствам выборочных характеристик главных компонент [2], [26], [14], [15], [20], [21], [4]. Если все характеристические корни ковариационной матрицы  различны, что и имеет место в большинстве приложений анализа главных компонент, то справедливо следующее:

— характеристические корни и соответствующие им собственные векторы выборочной ковариационной матрицы  являются оценками максимального правдоподобия для соответствую­щих теоретических характеристик (соответственно и ) и обладают всеми хорошими свойствами этих оценок (со­стоятельность, асимптотическая эффективность). Следовательно, выбо­рочные главные компоненты

(i = 1, 2,..., р)

можно интерпретировать как оценки главных компонент y⁽ⁱ⁾ всей ге­неральной совокупности. Если среди характеристических корней встречаются равные между собой, то оценки максимального правдоподобия для и определяются иначе. Аналогичные результа­ты имеют место и при оценке характеристических корней и соответст­вующих им собственных векторов корреляционной матрицы;

— величины

(i = 1, 2,..., р)

асимптотически (по п   ) нормальны со средним значением 0 и с дисперсией, равной 2, и независимы от других выборочных харак­теристических корней;

— вектор

(i = 1, 2,..., р)

асимптотически (по п   ) подчиняется многомерному нормальному распределению с вектором средних значений 0 и с ковариационной матрицей

Заметим, что этот результат имеет место для всякого отличного от всех остальных характеристических корней, каждый из которых может иметь произвольную кратность;

—выборочный характеристический корень распределен асим­птотически (по п  ) независимо от компонент соответствующего ему собственного вектора ( i = 1, 2, ..., р);

—ковариация между r-й компонентой выборочного собственного вектора и q-й компонентой выборочного собственного вектора , равна

.

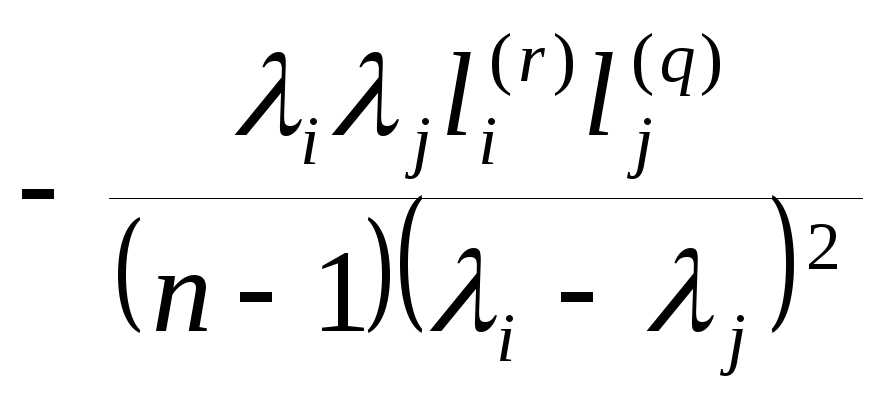Следующий факт [4] относится к весьма специфической ситуации, характеризуемой так называемым «эффектом большой размерности», когда, несмотря на достаточно большой объем выборки п, поведение выборочных характеристик обнаруживает неожиданные особенности из-за соизмеримо (с п) большого значения размерности р; при этом для вывода этого факта не требуется нормальности исходных наблюдений;

— если компоненты х⁽ⁱ⁾ вектора наблюдений Х взаимно незави­симы и пронормированы таким образом, что M х⁽ⁱ⁾ = 0 и D х⁽ⁱ⁾ = 1, причем существуют все моменты М (х⁽ⁱ⁾)^v, и если объем выборки п и размерность р одновременно достаточно велики, причем

(0  c ),

то распределение случайно выбранного из последовательности характеристического корня «слабо сходится»¹ к некоторому предельному распределению (сосредоточенному на конечном отрезке), моменты которого задаются формулой.

, (v=l, 2…)

так что и т. д. Здесьс—не­которая постоянная величина, причем 0  c < ).

Заметим, что примером подобного соотношения между объемом выборки и размерностью может служить задача, описанная в § 1 главы V, в которой п = 74, а р = 32 (так что (p/n) = 0,43).

В заключение приведем два факта, относящихся к ситуациям, в которых компоненты нормального вектора наблюдений Х взаимно не­зависимы:

— пусть ХN(a,), где ковариационная матрица имеет диагональ­ный вид, т. е. cov (x⁽ⁱ⁾, x^(j)) = 0 при i j, i, j = 1, 2, …, p. И пусть — определитель выборочной корреляционной матрицы, построен­ной по наблюдениям (Х₁, ..., Х_n). Тогда при достаточно больших n (п  ) статистика критерия отношения правдоподобия для провер­ки гипотезы о диагональном виде  может быть определена в виде

,

а для функции распределения спра­ведливо приближенное соотношение

при относительной ошибке, не превосходящей сотых долей процента;

— пусть наблюдения X_j извлечены из так называемой сферической р-мерной нормальной совокупности N (a, ²J), т. е. компоненты каж­дого из векторов X_j взаимно независимы и имеют одинаковые диспер­сии Dx_j⁽ⁱ⁾ равные ². Тогда ковариационная матрица  = ²J имеет единственный корень (кратности р), оценкой максимального правдо­подобия для которого является величина

(4.16)

причем величина ² распределена по закону ² (р (n — 1)).

Статистика критерия отношения правдоподобия для проверки ги­потезы о сферичности распределения исследуемого вектора наблюдений имеет вид

,

при достаточно больших n (п  )

и относительной ошибке данного приближенного соотношения, не превосходящей сотых долей процента.

б) Применения свойств выборочных характеристик главных компонент. Опишем некоторые методы построения разного рода интер­вальных оценок для интересующих нас неизвестных характеристик главных компонент и статистической проверки гипотез, относящихся к этим характеристикам:

- интервальная оценка (доверительный интервал) для i-гo ха­рактеристического корня _i. Она получается (при больших n) с учетом асимптотической нормальности статистики. А именно:

, (4.17)

где данное неравенство справедливо с вероятностью 1 —  (величиной  заранее задаемся), а — -ная точка стандартного нормального распределения (находится из таблиц).

Возвращаясь к примеру 1, по формуле (4.17), находим 95%-ный ( = 0,05) доверительный интервал для наименьшего характеристи­ческого корня ₃ по его выборочному значению ₃ = 2,86. В этом слу­чае п = 24, =1,96, так что 1,81 < ₃ < 6,78.

Возможно обобщение асимптотического (по п  ) доверитель­ного интервала на случай кратных, т.е. повторяющихся корней. Если r — кратность корня _i, то 100 (1 — ) — процентный доверительный интервал для неизвестного значения _i задается неравенством

, (4.18)

где

.

Однако откуда мы можем знать, что неизвестный характеристиче­ский корень _i имеет кратность и, в частности, кратность, равную r? Этот вопрос может быть решен с помощью следующего критерия, пред­ложенного в [15];

• проверка гипотезы о равенстве нескольких (а именно r) характе­ристических корней: _i = _i+1 = ... = _i+r-1. Очевидно, альтер­нативой к этой гипотезе является утверждение, что не все корни среди _i, _i+1, ..., _i+r-1 равны между собой. Оказывается, в предполо­жении справедливости проверяемой гипотезы статистика

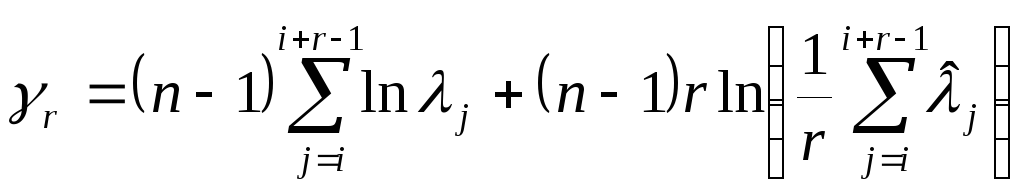(4.19)

распределена (асимптотически по п  ) по закону ² с (r(r+1)/2) — 1 степенью свободы. Поэтому гипотеза _i = _i+1 = ... = _i+r-1 отвергается (с вероятностью ошибиться, равной ), если

,

где _²(m) —100 %-ная точка ²-распределения с т степенями свободы.

Заметим, что особый интерес может представить специальный случай i = р — r + 1, т. е. проверка гипотезы о равенстве последних r собственных значений , что будет означать независимость и сферич­ность r последних признаков исследуемого вектора наблюдений.

Возвратимся к примеру 1. Тот факт, что оценка второго собствен­ного значения (₂ = 6,50) попадает в доверительный интервал для ₃ (см. выше), приводит нас к мысли, что, возможно, ₂=₃. Прове­рим эту гипотезу. В нашем случае n = 24, р = 3, i = 2, r = 2, так что

.

А поскольку (2) = 5,99 и, следовательно,

<(2),

то гипотезу ₂=₃ следует принять. Но тогда нужно пересчитать до­верительный интервал для ₂ с учетом его кратности (в соответствии с (4.18)). Несложные подсчеты (при  = 0,05 и, соответственно, =u_0,025 = 1,96) дают: 2,62  ₂ 6,21,

где последнее неравенство будет справедливо в среднем в 95 случаях из 100;

— проверка гипотезы о независимости признаков x⁽¹⁾, x⁽²⁾,…, x^(p), являющихся компонентами вектора наблюдений X. Такая проверка нужна для установления целесообразности применения метода главных компонент: ведь, если признаки являются взаимно независимыми, то переход к главным компонентам сведется по существу лишь к упорядо­чиванию исходных признаков по принципу убывания их дисперсий. Воспользуемся статистикой критерия отношения правдоподобия для проверки гипотезы о диагональном виде ковариационной матрицы с целью проверки независимости компонент вектора наблюдений в следующем примере.

Пример 2 [2]. Исследовалось время, затрачиваемое работника­ми швейной фабрики па выполнение различных элементов операции глаженья одежды. Операцию глаженья можно разделить на следу­ющие шесть элементов:

1) одежда размещается на гладильной доске (x⁽¹⁾);

2) разглаживаются короткие швы (x⁽²⁾);

3) одежда перекладывается на гладильной доске (x⁽³⁾);

4) разглаживаются длинные швы на три четверти (x⁽⁴⁾);

5) разглаживаются остатки длинных швов (x⁽⁵⁾);

6) одежду вешают на вешалку (x⁽⁶⁾).

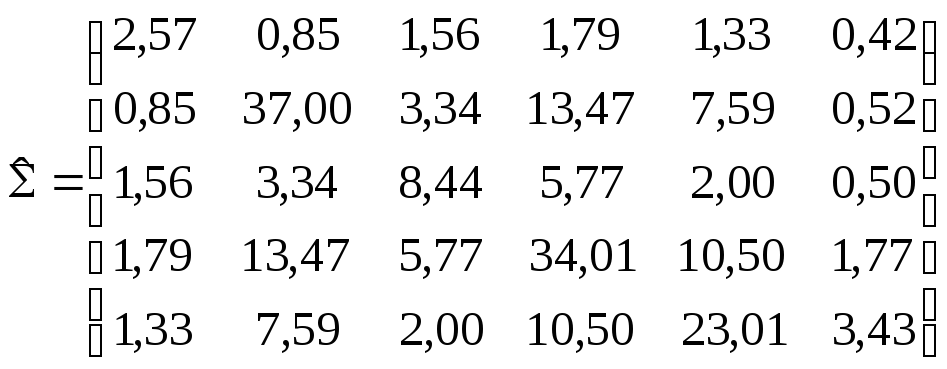
В этом случае Х_v представляет собой вектор измерения над v-м индивидуумом. Компонента x⁽ⁱ⁾—это время, затраченное на выпол­нение i-го элемента операции, n = 76. Данные (время в секундах) обработаны, получены выборочные вектор среднего значения и ковари­ационная матрица

.

Выборочные стандартные отклонения равны (1,604; 6,041; 2,903; 5,832; 4,798; 2,141). Выборочная корреляционная матрица R = (r_ij) имеет вид:

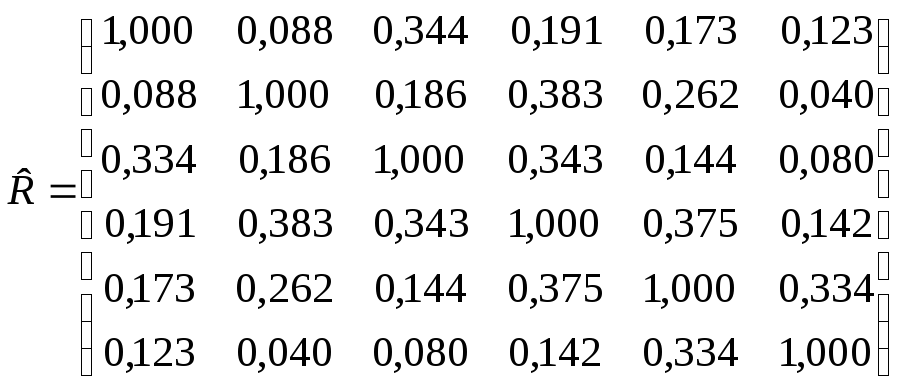
Для исследователей представляет интерес проверка гипотезы о вза­имной независимости шести случайных величин. Часто при изучении затрат времени предлагается новая операция, в которой элементы ком­бинируются иным способом. В новой операции некоторые элементы могут повторяться по нескольку раз, а некоторые могут быть выбро­шены. Если оказываются независимыми величины, обозначающие вре­мя, затрачиваемое на различные элементы операции, то естественно счи­тать, что и в новой операции они останутся независимыми. Тогда рас­пределение затрат времени на новую операцию можно будет оцепить, пользуясь средними значениями и дисперсиями, вычисленными для ос­тальных элементов. Кроме того, нас интересует возможность выделения небольшого количества вспомогательных признаков (двух-трех), с по­мощью которых мы могли бы производить некоторую содержательную классификацию исследуемых работников (в том или ином смысле).

В этой задаче отношение правдоподобия V равно = 0,472. Так как объем выборки велик, то можно пользоваться теорией асимптоти­ческих разложений.

В нашем случае , а р (р — 1)/2 = 15. Задавшись уровнем значимости кри­терия  = 0,01 (вероятность ошибочно отвергнуть проверяемую гипотезу), находим (из таблиц) величину 1%-ной точки ^2-распределения с 15 степенями свободы: (15) = 30,6. Поскольку  >(15), то гипотезу следует отвергнуть, т.е. приходим к выводу, что значения затрат времени на различные элементы операции нельзя считать независимыми;

—статистическая проверка некоторых предположений (гипотез) относительно собственных векторов l_{i ­}, ковариационной матрицы ис­следуемых признаков (i = 1, 2, ..., р). Пусть у нас есть основания пред­полагать, что «нагрузки» всех признаков на первую главную компонен­ту равны между собой (факт симметричной зависимости первой главной компоненты от исходных признаков), т. е.

,

или, напротив, что некоторые из признаков, скажем x^(p-1) и x^(p), во­обще не влияют на первую главную компоненту (т. е. l_1(p-1) = l_1p = 0), в то время как остальные р — 2 признака влияют на нее симмет­рично, т.е. и т.д.

Для решения подобных вопросов можно использовать статистиче­ский критерий равенства _­i-го собственного вектора неизвестной кова­риационной матрицы некоторому заранее заданному вектору . В [15] показано, что гипотеза l_i = должна быть отвергнута (с вероятностью ошибиться, т. е. с уровнем значимости критерия, приблизительно рав­ной а), если окажется, что

,

где подразумевается, что характеристический корень , оценка кото­рогоучаствует в выражении для критической статистики, имеет крат­ность, равную единице, а все остальные величины соответствуют ранее введенным обозначениям;

— проверка гипотезы о равнокоррелированности всех р исходных признаков, т. е. гипотезы r_ij = r⁽⁰⁾, где r_ij — парный коэффициент кор­реляции между признаком х⁽ⁱ⁾ и признаком x^(j) [26]. Эта гипотеза оз­начает, что последние р — 1 характеристических корней корреляцион­ной матрицы равны между собой. Кроме того, постулируемый здесь специальный вид корреляционной матрицы допускает простые явные выражения в виде решений соответствующих характеристических уравнений ( ₁ = 1+ (p-1)r⁰, ₂ =…=_p = 1- r⁰, y⁽¹⁾= (x⁽¹⁾+ x⁽²⁾+…+ x^(p)/и т.д. [26, с. 244]).

Оказывается, гипотезу r_ij = r⁽⁰⁾ следует отвергнуть (с вероятностью ошибиться, приблизительно равной ), если

,

где — выборочные парные коэффициенты корреляции между х⁽ⁱ⁾ и х^(j), подсчитанные по наблюдениям X₁, Х₂, .... Х_n, а

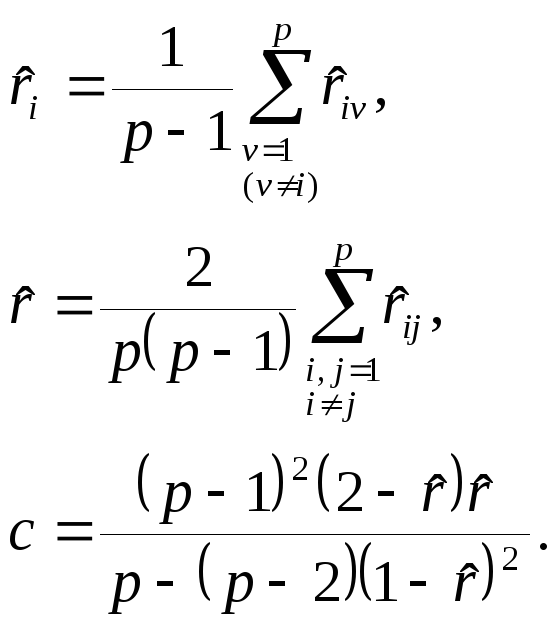
Кстати, в нашем примере 1 корреляционная матрица

Несложные подсчеты дают:

=0,9733, =0,9698,= 0,9691,=0,9707 так что в конечном счете = 0,825.

Задавшись уровнем значимости  = 0,05 и отыскав по таблицам (2) = 5,99, приходим к выводу, что гипотеза о равнокоррелированности всех трех исходных признаков может быть признана непротиворечащей имеющимся у нас результатам наблюдения.