2. Экстремальные свойства главных компонент. Их интерпретация

а) Свойство наименьшей ошибки «автопрогноза» или наилучшей самовоспроизводимости. Можно показать [27], [29], 128], что с помощью первых р' главных компонент y⁽¹⁾, y⁽²⁾, …,y^(p’) (р'<. р) исходных признаков x⁽¹⁾, x⁽²⁾,…, x^(p) достигается наилучший прогноз этих признаков среди всех прогнозов, которые можно построить с помощью р' линейных комбинаций набора из р произвольных признаков.

Поясним и уточним сказанное. Пусть мы хотим заменить исходный исследуемый p-мерный вектор наблюдений Х на вектор Y = (y⁽¹⁾, y⁽²⁾, …,y^(p’)) меньшей размерности р', в котором каждая из компо­нент являлась бы линейной комбинацией р исходных (или каких-либо других, вспомогательных) признаков, теряя при этом не слишком много информации. Информативность нового вектора Y зависит от того, в какой степени р' введенных линейных комбинации дают возмож­ность «реконструировать» р исходных (измеряемых на объектах) признаков. Естественно полагать, что ошибка прогноза Х по У (обозна­чим ее  ) будет определяться так называемой остаточной дисперсион­ной матрицей вектора Х при вычитании из него наилучшего прогноза по У, т.е. матрицей  = (_ij), где

.

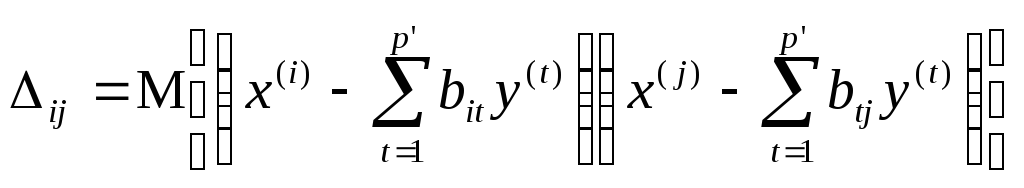Здесь — наилучший, в смысле метода наименьших квадратов, прогноз x⁽ⁱ⁾ по компонентам y⁽¹⁾, y⁽²⁾, …,y^(p’), т. е. =f(), где f() —некоторая функция (качества предсказания) от элементов остаточной дисперсионной матрицы .

Рао [29] решал задачу наилучшего прогноза Х только в классе р' линейных комбинаций от исходных признаков x⁽¹⁾, x⁽²⁾,…, x^(p) и рас­смотрел естественные меры ошибки прогноза, такие, как

f () = tr() = ₁₁ + ₂₂ + … + _pp (4.13)

и

(4.14)

tr () и называются соответственно следом и евклидовой нормой матрицы . Он показал, что функции (4.13) и (4.14) одновременно достигают минимума тогда и только тогда, когда в качестве y⁽¹⁾, y⁽²⁾, …,y^(p’) выбраны первые р' главных компонент вектора X, причем величина ошибки прогноза  явным образом выражается через последние р—р' собственных чисел _p’+1,…, _p исходной ковариа­ционной матрицы  или через последние р — р' собственных чисел _p’+1,…, _p выборочной ковариационной матрицы , построенной по наблюдениям X₁, Х₂, ..., Х_n. В частности,

при ;

при .

В работах [27] — [28] эта схема обобщена на случай произвольных предсказывающих признаков z⁽¹⁾,…, z^(p) и более широкого клас­са функций f() и показано, что min f() достигается тогда и только тогда, когда в качестве исходных предсказывающих признаков z⁽¹⁾,…, z^(p) берутся сами исследуемые (измеряемые) признаки x⁽¹⁾, x⁽²⁾,…, x^(p), а в качестве р' линейных комбинаций (предикторов) y⁽¹⁾, y⁽²⁾, …,y^(p’)от них выбраны первые р' главных компонент век­тора X. При этом величина ошибки прогноза , как и прежде, опреде­ляется лишь р—р' последними собственными значениями _p’+1,…, _p исходной ковариационной матрицы .

В эту схему укладывается, в частности, случай , в ко­тором, кстати,

Поясним идею описания (прогноза) исходных признаков x⁽¹⁾, x⁽²⁾,…, x^(p) помощью меньшего чем p числа их линейных комбина­ций на примере 1.

В этом примере, как мы видели, р = 3. Зададимся целью снизить размерность исходного факторного пространства до единицы (р' = 1), т.е. описать все три признака с помощью одной линейной комбинации от них.

В соответствии с описанным выше экстремальным свойством «автопрогноза» главных компонент возьмем в качестве этой единственной линейной комбинации первую главную компоненту, т. e, переменную

y⁽¹⁾=0,81x⁽¹⁾+0,50x⁽²⁾+0,31x⁽³⁾.

Метод наименьших квадратов приводит к следующему правилу вы­числения неизвестных коэффициентов b_i1 [1, с. 125].

Подставляя в эту формулу значения cov (x⁽ⁱ⁾, x^(j)), взятые из ковариационной матрицы  (см. стр. 141), получаем

x⁽¹⁾=b₁₁ y⁽¹⁾+⁽¹⁾=0,805 y⁽¹⁾+⁽¹⁾,

x⁽²⁾=b₂₁ y⁽¹⁾+⁽²⁾=0,493 y⁽¹⁾+⁽²⁾,

x⁽¹⁾=b₃₁ y⁽¹⁾+⁽³⁾=0,310 y⁽¹⁾+⁽³⁾,

где ⁽ⁱ⁾ — случайные (остаточные) ошибки прогноза исходных компонент по первой главной компоненте y⁽¹⁾.

Если в качестве относительной ошибки прогноза исходного признака x⁽ⁱ⁾ по первой главной компоненте y⁽¹⁾ рассмотреть величину _i =(D⁽ⁱ⁾/Dx⁽ⁱ⁾)·100%, то несложные подсчеты дают

₁ = 1%, ₂ = 2% и ₃ = 4%.

Суммарная характеристика относительной ошибки прогноза при­знаков x⁽¹⁾, x⁽²⁾ и x⁽³⁾ по y⁽¹⁾ (в соответствии с вышеописанным) может быть подсчитана по формуле

_{сум. отн.} = .

6} Свойства наименьшего искажения геометрической структуры исходных точек (наблюдений) при их проектировании в пространство меныией размерности р', «натянутое» на р' первых главных компонент. Всякий переход к меньшему числу (p') новых переменных, y⁽¹⁾, y⁽²⁾, …,y^(p’), осуществляемый с помощью линейного преобразования (мат­рицы) С = (c_ij), - I = 1,2, …, j= 1,2, ...,p, т.е.

или в матричной записи

Y =СХ (4.15)

нам удобнее будет рассматривать теперь как проекцию исследуемых наблюдений X₁, X₂, ..., X_n из исходного факторного пространства Х в некоторое подпространство меньшей размерности Y_р'.

Геометрическая интерпретация сформулированных выше экстре­мальных свойств «автопрогноза» (самовоспроизводимости) главных ком­понент позволяет получить следующие интересные факты.

Свойство 1. Сумма квадратов расстояний от исходных точек-наблюдений X₁, Х₂, ..., Х_n до пространства, натянутого на первые р' главных компонент, наименьшая относительно всех других подпрост­ранств размерности р', полученных с помощью произвольного линей­ного преобразования исходных координат.

Это свойство станет понятным (в свете вышеописанного экстремаль­ного свойства «автопрогноза»), если напомнить, что сумма квадратов расстояний от исходных точек до подпространства, натянутого на р' первых главных компонент, есть не что иное, как умноженная на п (об­щее число наблюдений) суммарная дисперсия остаточных компонент (ошибок прогноза) ⁽¹⁾, ⁽²⁾, ..., ^(p), следовательно, эта сумма квадра­тов равна п(). Наглядным пояснением это­го свойства может служить рис. 4.1а, на котором ось y⁽¹⁾ соответствует подпространству, натянутому на первую главную компоненту (т. e. р = 2 и р' = 1), а сумма квадратов расстояний до этого подпространст­ва есть сумма перпендикуляров, опущенных из точек, изображающих наблюдения X_i=, на эту ось (сама ось y⁽¹⁾ может быть ин­терпретирована в данном случае как линия ортогональной регрессии x⁽²⁾ по x⁽¹⁾), см. [1, с. 127].

Свойство 2. Среди всех подпространств заданной размерности р' (р'<р), полученных из исследуемого факторного пространства Х с помощью произвольного линейного преобразования исходных ко­ординат x⁽¹⁾, x⁽²⁾,…, x^(p), в подпространстве, натянутом на первые р' главных компонент, наименее искажается сумма квадратов расстоя­ний между всевозможными парами рассматриваемых точек-наблюдений.

Поясним это свойство. Пусть Y_p' (С) — подпространство размер­ности р', натянутое на координаты y⁽¹⁾, y⁽²⁾, …,y^(p’), получаемые из исходных координат x⁽¹⁾, x⁽²⁾,…, x^(p) с помощью произвольного линейного преобразования (4.15), а Y₁, Y₂, …, Y_n — проекции исходных наблюдений Х₁, ..., Х_n, в подпространство Y_p’ (С), т.е. запись исход­ных наблюдений в координатах подпространства Y_p’ (С).

Введем в рассмотрение величины

выражающие суммы квадратов расстояний между всевозможными па­рами имеющихся у нас наблюдений соответственно в исходном про­странстве Х и в подпространстве Y_p' (С).

Из простых геометрических соображений очевидно, что всегда

M_p’  M_p при р'<р.

Рассматривая в качестве меры искажения суммы квадратов попар­ных взаимных расстояний между точками-наблюдениями величину

М_p – М_p’(С),

можно показать (см. [29]), что

где Lp' — матрица размера р' x р, строками которой являются пер­вые р' собственных векторов l₁^’, l₂^’, …, l_p'^’ исходной ковариационной матрицы  (т.е. подпространство Y_p’ (L_p’) является подпространст­вом, натянутым иа первые р' главных компонент вектора наблюде­ний X).

Свойство 3. Среди всех подпространств заданной размерности p' (p' < p), полученных из исследуемого факторного пространства Х с помощью произвольного линейного преобразования исходных ко­ординат x⁽¹⁾, x⁽²⁾,…, x^(p), в пространстве, натянутом на первые р' глав­ных компонент, наименее искажаются расстояния от рассматриваемых точек-наблюдений до их общего «центра тяжести», а также углы между прямыми, соединяющими всевозможные пары точек-наблюдений с их общим «центром тяжести».

Поясним это свойство. Рассмотрим матрицу G размера (р х п) «центрированных» наблюдений . Здесь, как и прежде, —исходные наблюдения, а— среднее арифметическое по всем наблюдениям i-го признака, т.е.

.

Введем в рассмотрение матрицу размера (п Х п)

H – G’G = (h_iq), i, q = 1, 2,..., n.

Нетрудно установить геометрический смысл элементов этой ма­трицы:

–

это квадрат расстояния от точки-наблюдения до общего «центра тяжести» , а

–

величина, пропорциональная косинусу угла между прямыми, соединя­ющими точки Х_q и X_j с центром тяжести .

Если рассмотреть, кроме того, матрицу G(С) наблюдений Y₁, …, Y_n, являющихся проекциями исходных (центрированных) наблю­дений X₁, …, Х_n в подпространство Y_p’(С) и соответствующую ей матрицу Н (С) = G' (C)G (С), то оказывается, что

,

где под понимается, как обычно, евклидова норма матрицыA, а L_p’ соответствует ранее введенным обозначениям.

Кстати, из описанного выше следует, что естественной мерой отно­сительного искажения геометрической структуры исходной совокуп­ности наблюдений при их проектировании в пространство меньшей раз­мерности, натянутое на первые р' главных компонент, является ве­личина

,

либо величина

.

При неизвестной истинной ковариационной матрице  ее собственные значения следует заменить собственными значениями выборочной ковариационной матрицы 2 и соответственно снаб­дить «крышками» сверху характеристики x и  степени искажения гео­метрической структуры исследуемой совокупности наблюдений,