Глава 3. Аналитическая динамика

3.1. Общее уравнение динамики – уравнение Даламбера-Лагранжа

Пользуясь принципом Даламбера (Ч.3 Динамика), можно придать уравнениям движения форму уравнений равновесия, если к активным (заданным) и пассивным (реакции связей) силам присоединить силы инерции.

Пусть имеется СМТ с удерживающими и идеальными связями. Тогда для каждой МТ, входящей в СМТ, согласно принципу Даламбера можно записать:

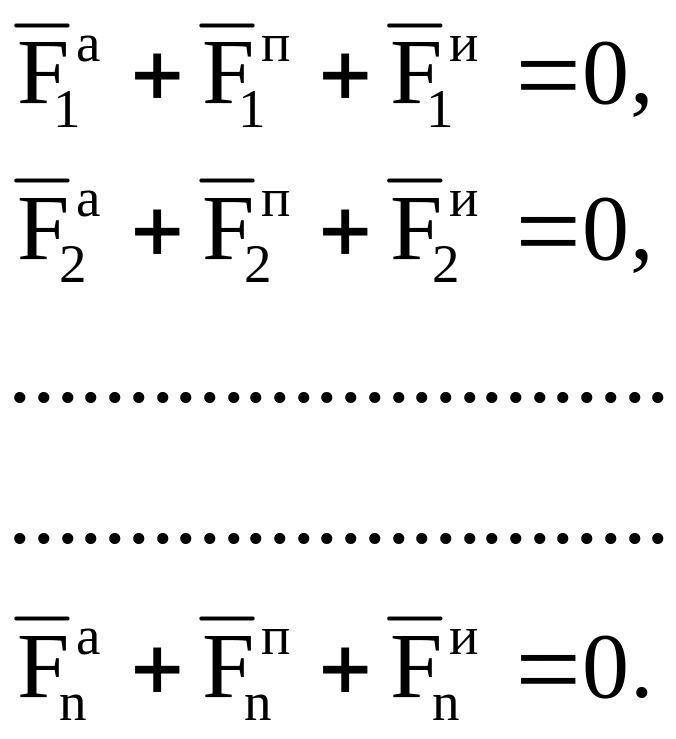(3.1)

Сообщив МТ, входящим в СМТ, виртуальные перемещения , умножим каждое из уравнений (3.1) на соответствующее , (=1,2,…,n) и сложим полученные выражения:

.

Так как связи, наложенные на СМТ, идеальные, то выполняются условия (1.12) и из предыдущего соотношения получаем общее уравнение динамики.

Общее уравнение динамики – уравнение Даламбера-Лагранжа:

При движении СМТ с удерживающими и идеальными связями, сумма элементарных работ всех активных сил, действующих на точки СМТ и условно приложенных к ним сил инерции на любом виртуальном перемещении равна нулю:

. (3.2)

Общее уравнение динамики можно представить также в виде:

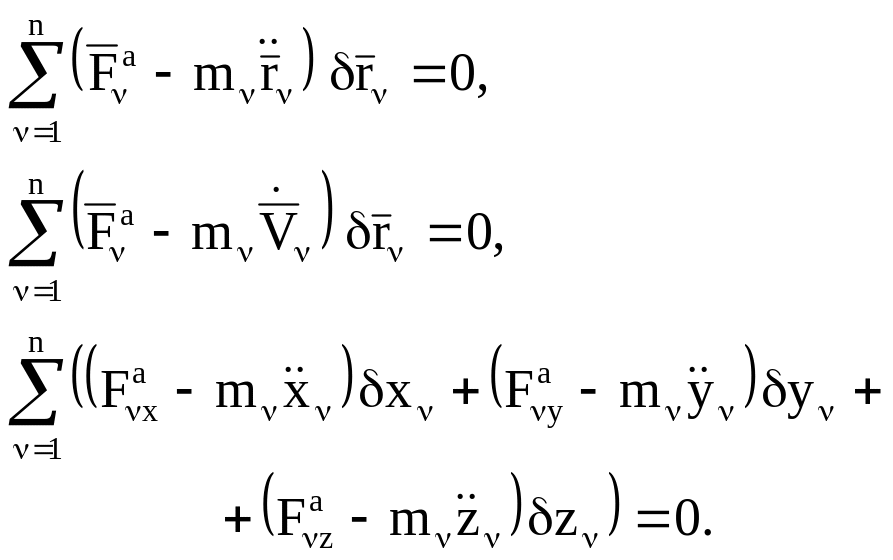(3.3)

Следует также отметить, что в случае удерживающих и неидеальных связей, общее уравнение динамики примет вид:

, (3.4)

где пассивные силы – силы реакции неидеальных связей.

Принцип виртуальных перемещений является частным случаем общего уравнения динамики (в случае равновесия СМТ сила инерции ).

3.2. Уравнения движения смт в обобщенных координатах – уравнения Лагранжа второго рода

Из общего уравнения динамики (соотношения (3.2), (3.3)) можно вывести дифференциальные уравнения движения СМТ в обобщенных координатах, подобно тому, как из принципа виртуальных перемещений (2.1) были выведены условия равновесия СМТ в обобщенных координатах (2.6).

Используем следующую форму общего уравнения динамики:

. (3.5)

Пусть на СМТ, имеющую  степеней свободы, нало­жены голономные, удерживающие и идеальные связи. Введем в рассмотрение  обобщенных координат q_ (=1,…,) и выразим через них радиус-вектор -й МТ аналогично тому, как это было представлено в формуле (1.13):

, .

Варьируя это соотношение, получим:

, . (3.6)

Подставляя соотношение (3.6) в соотношение (3.5) и изменяя порядок суммирования, имеем:

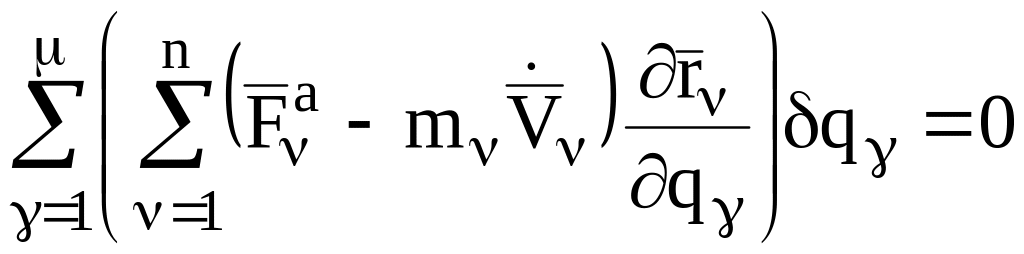. (3.7)

Так как все независимы и произволь­ны, то равенство (3.7) может выполняться только тогда, когда каждый из коэффициентов при равен нулю, поэтому нахо­дим:

.

Эту систему  уравнений запишем в виде:

. (3.8)

Правая часть соотношения (3.8) представляет собой обобщенную силу (формула (1.16)) соответствующую обобщенной координате :

. (3.9)

Преобразуем выражение, входящее в левую часть соотношения (3.8) следующим образом:

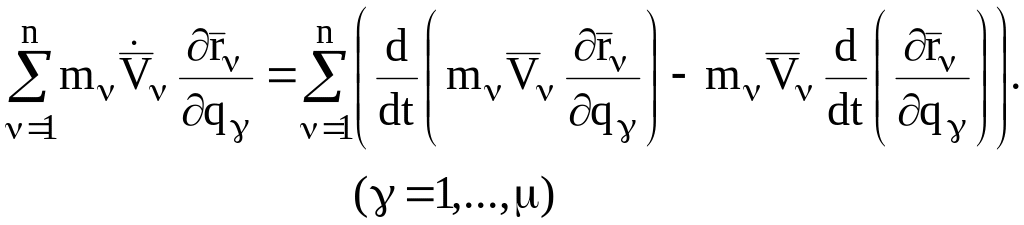(3.10)

Учитывая, что радиус-вектор -й МТ зависит от времени t сложным образом, получим следующее выражение для ее скорости движения:

, (3.11)

где – называется обобщенной скоростью ( = 1, 2,…, ).

Так как множители ( = 1, 2,…, ) зависят только от обобщенных координат и времени t (и не зависят от обобщенных скоростей), то дифференцируя правую и левую часть соотношения (3.11) по обобщенной скорости , приходим к соотношению:

. (3.12)

Найдем частную производную скорости по обобщенной координате , учитывая, что обобщенные координаты входят в правую часть равенства (3.11) через коэффициенты при обобщенных скоростях:

. (3.13)

Частная производная зависит от времени t явно и через обобщенные координаты , ( ). Вычисляя полную производную по времени от частной производной, находим:

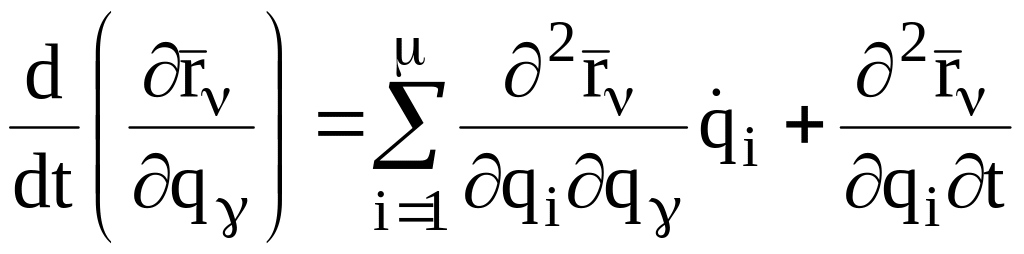. (3.14)

Сравнивая правые части выражений (3.13) и (3.14), замечаем, что

. (3.15)

Возвращаясь к формуле (3.10) и подставляя в нее тождества (3.12) и (3.15), получаем:

.

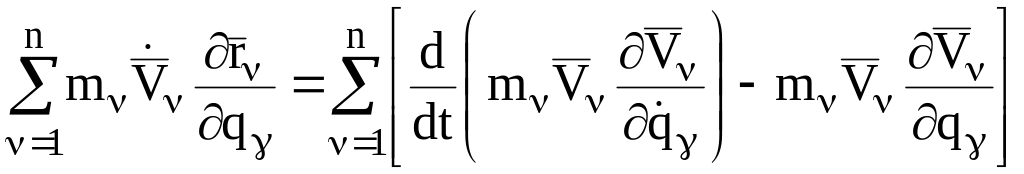Учитывая, что

и

приведем последнее равенство к виду:

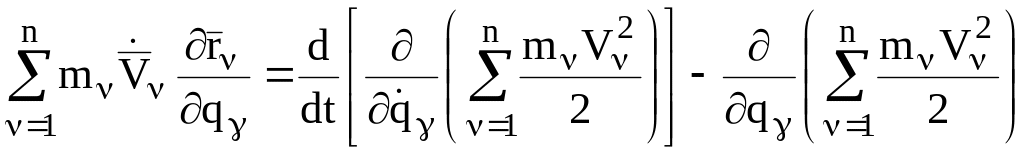. (3.16)

Кинетическая энергия СМТ (Ч. 3 Динамика) определяется формулой:

,

тогда (3.16) примет вид:

. (3.17)

Подставляя выражения (3.9) и (3.17) в уравнения (3.7), получим:

. (3.18)

Уравнения (3.18) представляют собой дифференциальные уравнения движения СМТ в обобщенных координатах. Эти уравнения называют уравнениями Лагранжа второго рода.

При наличии голономных связей, наложенных на систему, число уравнений Лагранжа второго рода равно числу независимых обобщен­ных координат, т. е. числу степеней свободы этой голономной системы.

Кинетическая энергия системы при подстановке в эти уравнения должна быть предварительно выражена как функция обобщенных скоростей и координат . Это будет квадратичная функция обобщенных скоростей , в коэффициенты которой могут входить обобщенные координаты (в частных случаях кинетическая энергия может быть квадратичной функцией скоростей с постоянными коэффициен­тами). Обобщенные силы тоже могут быть в общем случае функция­ми обобщенных координат , и скоростей . Таким образом, в выражения , и могут входить обобщенные координаты и их производные . Поэтому в выражение войдут уже вторые производные . Следовательно, уравнения Лагранжа второго рода (3.18) представляют собой обыкновенные дифференциальные уравнения второго порядка относительно обобщенных координат .

Основные преимущества уравнений Лагранжа второго рода (3.18) состоят в следующем. Во-первых, они дают единый и притом достаточно простой метод решения задач динамики для любых как угодно движущихся СМТ с голономными связями. Во-вторых, число уравнений (3.18) не зависит от числа МТ, входящих в СМТ и равно числу степеней свободы системы (в машинах, механизмах и приборах обычно одна, две и редко больше двух степеней свободы). В-третьих, силы и моменты, действующие на систему, представлены здесь в виде обобщенных сил, в которые входят только активные силы и моменты, а все реакции идеальных связей автоматически исключаются из уравнений. Этими преимуществами и объясняется широкое применение уравнений Лагранжа второго рода во всех технических науках и в ряде разделов физики.

Уравнениями Лагранжа второго рода можно пользоваться и в случаях, когда на систему наложены неидеальные связи, например связи с трением скольжения и качения. В этом случае силы и моменты неидеальных связей включаются в число активных сил и моментов.

Запишем теперь уравнения (3.18) для консервативных голономных СМТ. В этом случае обобщенные силы могут быть выражены через потенциальную энергию СМТ:

,

и, следовательно, уравнения (3.17) примут вид:

, (3.19)

Принимая во внимание, что потенциальная энергия системы зависит от обобщенных координат и не зависит от обобщенных скоростей , можно еще более упростить вид уравнения (3.19):

. (3.20)

Введем понятие кинетического потенциала (иначе называемого функцией Лагранжа):

L_к = T – П,

тогда уравнения (3.20) можно написать в форме:

. (3.21)

Уравнения (3.21) представляют собой уравнения Лагранжа второго рода для консервативных систем.