Глава 2. Аналитическая статика

2.1. Принцип виртуальных перемещений

Принцип виртуальных перемещений:

Для равновесия СМТ, на которую наложены стационарные, удерживающие и идеальные связи, необходимо и достаточно, чтобы сумма элементарных работ всех активных сил, действующих на СМТ, на любом виртуальном перемещении была равна нулю:

, (2.1)

Доказательство необходимости:

Для доказательства необходимости принципа предположим, что несвободная СМТ со стационарными, удерживающими и идеальными связями находится в положении равновесия. Тогда каждая МТ, входящая в СМТ, находится в равновесии и, используя аксиому 5 – принцип освобождаемости (Ч.1 Статика), можно записать:

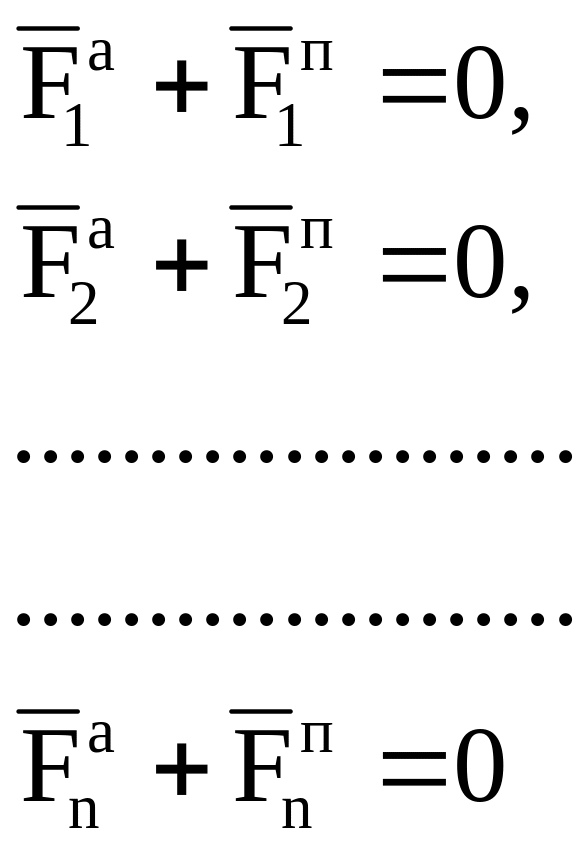(2.2)

Сообщив МТ, входящим в СМТ, виртуальные перемещения , умножим скалярно каждое из уравнений (2.2) соответственно на , (=1,2,…,n) и сложим полученные выражения:

.

Так как связи, наложенные на СМТ, идеальные, то выполняются условия (1.12) и из предыдущего соотношения получаем уравнение:

.

Что и требовалось доказать.

Доказательство достаточности:

Для доказательства достаточности применим метод от противного. Предположим, что при выполнении условия (2.1) СМТ не находится в равновесии, и хотя бы одна из МТ, например первая, пришла в движение. Тогда для этой МТ условие типа (2.2) выполняться не будет, т.е.:

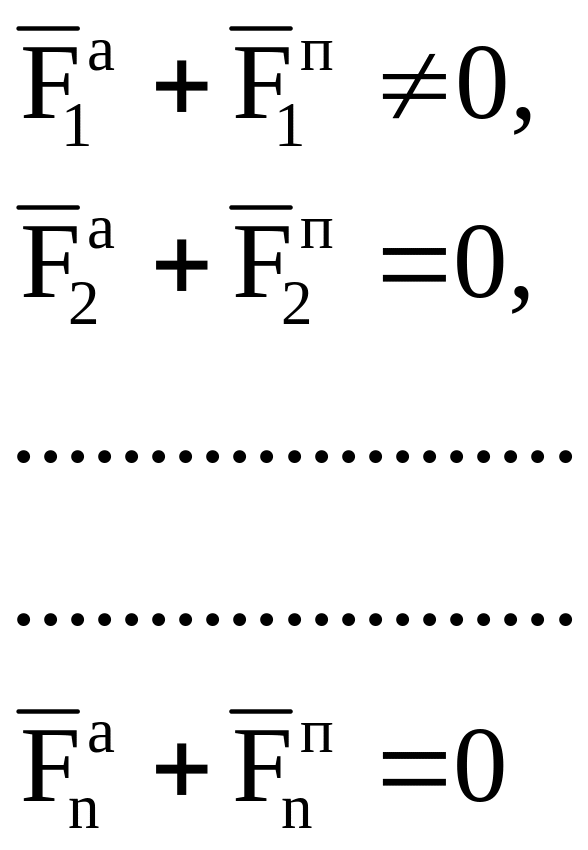(2.3)

Сообщив МТ, входящим в СМТ, виртуальные перемещения , умножим каждое из уравнений (2.3) на соответствующее , (=1,2,…,n) и сложим полученные выражения почленно:

.

Так как связи, наложенные на СМТ, идеальные, то выполняются условия (1.12) и из предыдущего соотношения получаем неравенство:

,

а это противоречит условию (2.1). Следовательно, наше предположение о том, что при выполнении условия (2.1) СМТ не находится в равновесии, неверно, т.е. выполнение этого условия является и достаточным для равновесия СМТ.

Следует отметить, что в случае стационарных, удерживающих и неидеальных связей, принцип виртуальных перемещений примет вид:

(2.4)

где – пассивные силы – силы реакции неидеальных связей.

2.2. Условия равновесия смт в обобщенных координатах

Запишем выражение принципа виртуальных перемещений (2.1) с учетом соотношения (1.17):

. (2.5)

Так как вариации обобщенных координат независимы и произвольны, то уравнение (2.5) выполняется только при условии, что все обобщенные силы равны нулю. В этом легко убедиться, сообщив СМТ виртуальное перемещение, при котором вариации всех обобщенных координат, кроме одной, например первой, равны нулю

(2.6)

Подставляя (2.6) в (2.5) получим и так далее для всех обобщенных сил. В результате приходим к следующим условиям равновесия СМТ в обобщенных координатах.

Условия равновесия СМТ в обобщенных координатах:

Для равновесия СМТ, на которую наложены стационарные, удерживающие и идеальные связи необходимо и достаточно, чтобы все обобщенные силы равнялись нулю:

. (2.7)

Следует отметить, что в случае неидеальных связей в условия равновесия СМТ в обобщенных координатах войдут пассивные силы и моменты реакции связей.