Федеральное агентство по образованию

Государственное образовательное учреждение высшего профессионального образования

ТЮМЕНСКИЙ ГОСУДАРСТВЕННИЙ АРХИТЕКТУРНО-СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ

Кафедра физики

Методические указания к лабораторной работе № 1-мех.

«Элементарные оценки погрешностей измерений»

Составила:

Самсонова Н.П.

Тюмень 2004г.

ЛАБОРАТОРНАЯ РАБОТА № 1-мех.

ЭЛЕМЕНТАРНЫЕ ОЦЕНКИ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЙ.

ЦЕЛЬ РАБОТЫ:	измерение объема цилиндра и расчет погрешности измерений.
ОБОРУДОВАНИЕ:	цилиндр, микрометр, штангенциркуль.

ВВЕДЕНИЕ

ИЗМЕРЕНИЕМ какой-либо физической величины называется операция, в результате которой мы узнаём, во сколько раз измеряемая величина больше (меньше ) соответствующей .величины, принятой за единицу.

Различают ПРЯМЫЕ и КОСВЕННЫЕ измерения. При прямых измерениях определяемая величина сравнивается с единицей измерения непосредственно или при помощи измерительного прибора, проградуированного в соответствующих единицах. К прямым относятся, например, измерение длины детали линейкой, измерение силы тока амперметром и т.д.

'При косвенных измерениях измеряемая величина определяется (вычисляется ) из результатов измерения других величин, которые связаны с измеряемой величиной определенной функциональной за­висимостью. К косвенным относятся, например, измерение площади прямоугольника S через его длину a и ширину в, измерение напряжения U = IR через, силу тока I в резисторе с сопротивлением R.

Никакое измерение не может быть проведено абсолютно точно. Его результат всегда содержит некоторую ошибку (погрешность). Погрешности измерений принято подразделять на СИСТЕМАТИЧЕСКИЕ и СЛУЧАЙНЫЕ.

Систематические ошибки происходят от несовершенства приборов и недостаточно разработанной теории .опыта (влияние среды, роль примесей, контакты с другими телами и т.п.). Они вызывают от­клонение результатов от истинного значения только в одну сторо­ну (или в сторону увеличения, или в сторону уменьшения).

Случайные ошибки обусловлены неточностью считывания дан­ных и другими отклонениями, носящими вероятностный характер. Случайные ошибки могут изменять результаты в обе стороны, то увеличивая, то уменьшая их. Уменьшить влияние случайных ошибок на окончательный результат можно за счет увеличения числа изме­рений.

Обработка результатов измерений проводится различными спо­собами, в зависимости от того, являются измерения прямыми или косвенными.

Определение погрешностей прямых измерений

Пусть в результате n измерений некоторой величины x получены её значения x₁, x₂, x₃, …, x_n. В теории погрешностей в качестве результата прямых измерений используют среднее арифметическое значение

. (1)

Истинное значение величины x не совпадает со средним (оно может совпадать только в отсутствие систематических ошибок и при бесконечно большом числе измерений). Однако всегда можно указать интервал , в который с заданной вероятностью попадает истинное значение x.

Величина называется ДОВЕРИТЕЛЬНЫМ ИНТЕРВАЛОМ, или АБСОЛЮТНОЙ ПОГРЕШНОСТЬЮ, она характеризует качество проведенных измерений.

Вероятность того, что истинное значение x попадает в данный доверительный интервал, называется ДОВЕРИТЕЛЬНОЙ ВЕРОЯТНОСТЬЮ (обозначается ), или НАДЕЖНОСТЬЮ результатов изме­рений. Величина  выражается или в долях единицы, или в процентах. Её значение задает экспериментатор, в физических опытах обычно  =0.95 или 95%.

Абсолютная погрешность складывается из случайной х_сл. и систематической х_сист. погрешностей

(2)

Случайная погрешность х_сл. пропорциональна среднеквадратичной ошибке ,

(3)

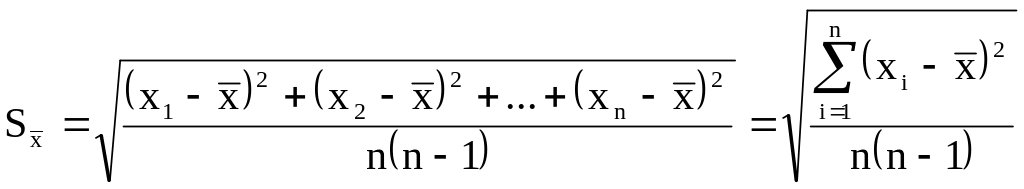(4)

и характеризует разброс результатов измерений вокруг среднего.

Коэффициент пропорциональности называется коэф­фициентом Стьюдента, он характеризует зависимость погрешности х_сл. от числа измерений n и величины надежности . Коэффициенты для различных n и  рассчитаны в тео­рии вероятностей, их значения берутся из таблиц.

Систематическая погрешность х_сист. принимается равной

, (5)

 - погрешность прибора.

Приборная погрешность определяется на основе паспортных данных прибора, его класса точности и т.д.

Если класс точности прибора не указан, погрешность  бе­рут равной половине цены деления шкалы прибора.

Окончательно, с учетом формул (2), (3), (5), абсолютная пог­решность измерений

. (6)

Результат прямых измерений записывается в виде:

с надежностью .

Для оценки качества измерений также рассчитывают относитель­ную погрешность ,

(7)

которая показывает, какой процент от измеряемой величины состав­ляет абсолютная погрешность.

ОПРЕДЕЛЕНИЕ ПОГРЕШНОСТЕЙ КОСВЕННЫХ ИЗМЕРЕНИЙ.

Допустим, необходимо косвенно измерить величину F, кото­рая известной функциональной зависимостью связана с независимы­ми величинами x, y, z, …, F=f(x, y, z, …).

Чтобы провести расчет этой величины и оценить погрешность её измерений, вначале необходимо рассчитать средние значения аргументов и их абсолютные погрешности по схеме расчета для прямых измерений.

Наиболее достоверным значением величины F является сред­нее , которое рассчитывается путем подстановки средних зна­чений аргументов в формулу для расчета F,

. (8)

Абсолютную погрешность F косвенных измерений рассчитывают по формуле

(9)

где - абсолютные погрешности величин x, y, z, …, производные вычисляются по средним арифметическим значениям аргументов. Окончательно результат косвен­ных измерений представляют в форме

. (10)