Бета-функция.
С гамма-функцией
тесно связана бета-функция
.
Определение5.3.3:
бета-функцией называется несобственный
интеграл, который зависит от двух
параметров :
(5.3.3.1) (4)
(интеграл в правой
части равенства (5.3.3.1) называется
Эйлеровым интегралом первого рода).
Интеграл (5.3.3.1)
сходится при
.
Другое аналитическое представление бета-функции.
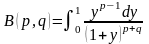(5.3.3.2)
Выражение бета-функции через гамма-функцию.
Бета-функция может быть легко выражена через гамма-функцию.
(5.3.3.3)
;
разделим обе части этого равенства на
и положим
;тогда
(*)
положим в (*)
:
;
откуда
и т.д. – см. «Избранные главы высшей
математики» стр. 100-101.
Из формулы (5.3.3.3.)
вытекает интересное следствие: положив
,
получим
,
но
,
поэтому имеем:
Итак,
;
(перед корнем знак «+», так как при
,
).
Отсюда в свою
очередь можно вывести значение важного
интеграла
.
.Следовательно,
.
Замечание:
в приложениях функцию
обычно сводят к гамма-функции.
И гамма-функция и бета-функция широко используются при вычислении определенных интералов
Пример 5.3.4:
доказать, что
при любом действительном числе
.
Решение
Пример 5.3.5:
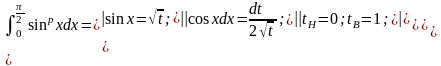
Докажем, что
интеграл
сходится при
(№1575,Демидович.):
(промежуточная точка
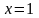
взята лишь из соображений удобства, её роль могла играть любая другая). Исследуемый интеграл будет сходиться, если будут сходится оба интеграла в правой части. Первый интеграл есть несобственный интеграл от неограниченной функции, так как при
функция
,
если
.
Так как
и
(при
)
сходится, то и интеграл
сходится при
.
является несобственным интегралом с
бесконечным промежутком интегрирования.
По принципу сравнения
можно доказать, что он сходится при
-произвольном.(№1574,Демидович): Докажем, что сходится при
.
.
Приложения определенного интеграла.
Определенный интеграл имеет разнообразные приложения в области геометрии (вычисление площадей, объемов, длин кривых) и механики (вычисление работы переменной силы и др.). мы рассмотрим некоторые из них.
6. Геометрические приложения определенных интегралов.
6.1. Вычисление площадей плоских фигур.
Площадь криволинейной трапеции, ограниченной кривой
y = f(x) [f(x) ≥0], двумя ординатами x = a и х = b и определить [a,b] оси OX ,вычисляется по формуле
S
=
Площадь фигуры, ограниченной двумя кривыми y = f1(x) и y = f2(x) и двумя вертикалями x=a и x=b находятся по формуле
S
=
Если кривая задана параметрическими уравнениями х = х(t), у =у(t),то площадь криволинейной трапеции, ограниченной этой кривой, ординатами х = а ,у =b и отрезанном [a,b] оси ОХ ,выражается формулой
S
=
Где t1 и t2 определяются из уравнений
a =x(t) b =x(t) [ y(t) ≥0 при t1 ≤ t ≤ t 2 ]
Площадь криволинейного сектора ,ограниченного кривой, заданной в полярных координатах уравнением ρ =ρ(θ) и двумя полярными радиусами θ = α, θ = β (α< β) выражается интегралом
S
=
6.1.1.Вычислить площадь, ограниченную следующими линиями
у = - х2 +4 и у = 0
Решение. Выполним построение фигуры.
Искомая площадь заключена между параболой у = - х2 +4 и осью Ох
Найдём точки пересечения карболы с осью Ох.Положив у=0 ,найдём х= ±2.
Имеем:
F(x) = -x2+4, a=2 и b=-2:
(кв.ед.)
Парабола симметрична относительно оси Оу ,поэтому можно вычислить площадь, ограниченной параболой и осями Ох и Оу и полученный результат удвоить:
S1
=
(кв.ед.);
S
=2S1
=
(кв.ед.)
6.1.2. Вычислить площадь ограниченную синусоидой y=sin x и осью Ох, при 0≤х≤2π.
Решение.
Так как sin x≥ 0 при 0≤x≤π≤ и
sin≤0 при π≤ x≤2π,то
S
=
=
=
=
Следовательно S =2+|-2|=4
6.1.3. Вычислить площадь фигуры ,ограниченную линиями y=x2 и у=2х+8.
Решение. Выполним построение фигуры .
Для похождение точек пересечение параболы у=х2 и прямой у=2х+8 решим систему уравнения относительно x:
x2
=2x+8
x1
=-2 x2
=4
Искомая
площадь представляет собой разность
площадей:
.Пределы
интегрирования : а=х1=-2,
b=x2
=4
6.1.4.Вычислить площадь ограниченную кубическими параболами
6х=у3-16у и 24х=у3 – 16у
Решение: Решая совместно уравнения этих линий находим три точки пересечения данных парабол:
О(0;0), А(0;4), В(0;4).
Построим эти точки и параболы.
Искомая площадь состоит из двух одинаковых частей; половину её можно найти как разность площадей криволинейных трапеция ОСВ и ОДВ ,прилежащих к оси Оу. Согласно формулы имеем
6.1.5.Вычислить площадь ограниченную эллипсом
Решение. Оси координат совпадают с осями симметрии данного эллипса, и поэтому они делят его на четыре одинаковые части.
Четвёртую часть искомой площади, расположенную в первом квадрате, найдём как площадь криволинейной трапеции, прилежащей к оси Ох:
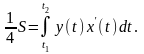
когда
то
когда
,то
Следовательно площадь данного эллипса выразится формулой
Отсюда
при
получается
формула для площади круга
6.1.6.Найти
площадь, ограниченную осью Ох и одной
«аркой»циклоиды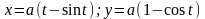
Решение. Когда круг, производящий циклоиду, сделает полный оборот, абсцисса той точки окружности круга, которая в начале движения совпадала с началом координат, станет равной 2πα( α -радиус окружности)
В
формуле надо взять
.Пределы
интегрирования будут равны 0 и 2π ,т.к.
параметр t
при одном
полном обороте производящего круга
пробегает отрезок [0;2π].Поэтому
Таким образом, искомая площадь в три раза больше площади катящегося круга.
6.1.7.Определить
площадь, ограниченную лемнискатой
Бернулли, определяемое уравнением
Решение. Лемниската-это геометрическое место точек произведение расстоянии каждой из которых от двух фиксированных точек(фокусов)-постоянная величина.
Проследим,
как изменяется угол
,
когда радиус-вектор точки на лемнискате
описывает четверть искомой площади,
лежащей в первой четверти.
При
.Определим
,чему равен полярный угол φ,
когда радиус вектора станет равным
нулю.. Подставляя
в
уравнение лемнискаты, получим
,откуда
;
;
Таким
образом,на одной четверти площади
полярный угол
изменяется от
до
.
Поэтому четверть искомой площади
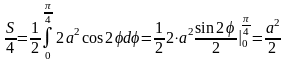
а вся площадь
6.1.8.Вычислить
площадь одного лепестка розы, определяемое
уравнением
Решение.
Кривые,
определяемые уравнение
,а
также уравнением
,где
α и
k
–постоянные
величины, называются розами. Если k
–чётное
число, то кривая имеет 2k
лепестков,
если же k
то кривая
имеет R
лепестков.
Чтобы
найти площадь одного лепестка, определим,
как изменяется полярный угол
Положим
и решим уравнение
Из
чего следует что
,а
отсюда
.При
,при
имеем
,а
.
Таким
образом, угол
изменяется от
до
,а
площадь одного лепестка равна
а)
для четырёхлепестковой розы
б)
для трёхлепестковой розы
