5. Несобственные интегралы

Понятие определенного интеграла было установлено для случая конечного промежутка и непрерывной на нем функции .

Это определение не применимо, если промежуток интегрирования бесконечен или функция в промежутке интегрирования имеет точки разрыва.

Между тем не редко возникает необходимость обобщить понятие неопределенного интеграла на тот случай, когда функция рассматривается на бесконечном промежутке, а также когда данная функция разрывна в промежутке интегрирования.

Эти обобщения приводят к так называемым несобственным интегралам, имеющим важное значение во многих областях математического анализа и его приложений.

5.1 Несобственные интегралы с бесконечными пределами интегрирования. Пусть функция определена и непрерывна в промежутке , т.е. для

Рассмотрим определенный интеграл от функции на отрезке при любом 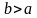: , он существует.

Так как верхний предел интеграла (1) переменный ( - любое число), то он является функцией верхнего предела: . Относительно этой функции возможны два следующих случая: или при функция , т.е. интеграл (1), имеет конечный предел, или эта функция (этот интеграл) такого предела не имеет (стремится к или вовсе не стремится ни к какому пределу).

Определение 5.1: предел интеграла (1) (конечный или бесконечный) при называют несобственным интегралом от функции в пределах от до и обозначают символом: .

Следовательно, по определению, .

В случае если предел (2) конечен, говорят, что несобственный интеграл сходится, а сам предел называют значением несобственного интеграла. Функцию называют тогда интегрируемой в бесконечном промежутке . Если же конечного предела (2) не существует, то говорят, что расходится.

Расходящемуся несобственному интегралу не приписывают никакого числового смысла.

Выяснение того вопроса, сходится ли несобственный интеграл или нет, называют исследованием интеграла на сходимость.

Пример 5.1.1:

Следовательно, сходится (существует) и имеет значение равно 1.

Мы определили несобственный интеграл от функции на бесконечном промежутке .

Аналогично определяется несобственный интеграл и для функции , заданной на бесконечном промежутке :

(где ).

Терминология, введенная выше в связи с рассмотрением интеграла , переносится и на этот интеграл.

Определим теперь интеграл для функции, заданной на интервале .

Пусть - произвольное число, и несобственные интегралы и сходятся. Тогда полагаем по определению:

(5.1)

Замечание: значение суммы интегралов, стоящих в правой части этого равенства, не зависит от выбора точки . В чем легко убедится (см. Уваров, стр. 536).

Пример 5.1.2:

Следовательно, интеграл сходится и его значение равно .

Во многих случаях бывает достаточно установить, сходится данный интеграл или расходится, и оценить его значение. Для этого пользуются следующими тремя теоремами (первые две теоремы для неотрицательной функции): Теорема5.1.1(признак сравнения): если , , то из сходимости интеграла следует сходимость интеграла , причем 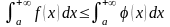(5.1.1)

Пример 5.1.3: исследовать, сходится ли интеграл . При , (при функция бесконечно малая по сравнению с

.

Так как этот несобственный интеграл сходится, то по теореме 1 делаем вывод, что и данный несобственный интеграл сходится; его значение меньше единицы. Теорема5.1.2 (признак сравнения): если для всех выполняется неравенство , то из расходимости интеграла следует расходимость интеграла

Замечание: теоремы 5.1.1 и 5.1.2 для определенности мы рассматривали для интеграла вида ; однако без существенных изменений они переносятся и на интегралы видов и .

Пример5.1.4: исследовать, сходится ли интеграл . Замечаем, что при 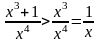. . Следовательно, этот интеграл а значит и данный, расходится.

Пусть функция меняет знак на бесконечном промежутке. Тогда имеет место следующая теорема:

Теорема5.1.3: если интеграл сходится, то сходится и интеграл , притом абсолютно.

Как видим, для знакопеременной функции можно установить лишь абсолютную сходимость. Если интеграл от данной функции расходится или сходится, но не абсолютно, то различить эти случаи с помощью рассмотренной выше теоремы нельзя. На практике удобно пользоваться следующей теоремой: Теорема(*): если существует предел , , то интегралы и одновременно или сходятся, или расходятся. Пример(*’): исследовать на сходимость . Поскольку , то данный интеграл расходится.

Замечание: сходится при 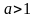и расходится при 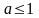, но это справедливо для интегралов с бесконечными пределами., а для интегралов с конечными пределами уже не будет так. При установлении сходимости или расходимости несобственного интеграла с помощью этой теоремы часто пользуются интегралом , , который для сходится, а для расходится.

Пример5.1.5: исследовать на сходимость . имеем: 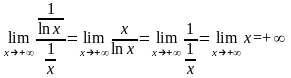. Так как интеграл расходится (см. пример выше), то будет расходится и данный интеграл.