
- •1 Определённый интеграл
- •1. Задачи, приводящие к понятию определённого интеграла.
- •Площадь криволинейной трапеции.
- •1.2. Понятие определенного интеграла.
- •1.3. Теорема существования определенного интеграла (без доказательства).
- •1.4. Основные свойства определенного интеграла.
- •2.Произвольная от определённого интеграла по переменному верхнему пределу.
- •3. Формула Ньютона-Лейбница.
- •4. Интегрирование по частям в определенном интеграле.
- •5. Несобственные интегралы
- •5.2 Несобственные интегралы от разрывных функций
- •5.3Интегралы, зависящие от параметра. Рассмотрим интеграл вида
- •Бета-функция.
- •Приложения определенного интеграла.
- •6. Геометрические приложения определенных интегралов.
- •6.1. Вычисление площадей плоских фигур.
- •6.2. Длина дуги.
- •6.3.Вычисление объёмов тел вращения.
- •6.4. Вычисление объемов тел по известным поперечным сечениям
- •6.5.Площадь поверхности вращения.
- •7. Приложения определенных интегралов к решению задач физики.
- •7.1.Путь пройденный телом
- •7.2.Работа силы
- •7.3. Количество электричества.
- •7.4. Вычисление давления
- •7.5. Кинематическая энергия
- •7.6. Статический момент.
- •7.7.Координаты центра тяжести.
- •8.Тестовые задания для самостоятельной работы.
- •9. Физические задачи для самостоятельной работы
- •10. Приближенные методы вычисления определенных интегралов.
- •450062, Республика Башкортостан, г. Уфа, ул. Космонавтов,1
2.Произвольная от определённого интеграла по переменному верхнему пределу.
Пусть
функция
интегрируема на отрезке
,
т.е. существует
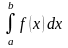
Из самого определения как предела интегральной суммы следует, что если функция и пределы интегрирования а и b заданы, то интеграл определяется однозначно (есть постоянное число), и значение его не зависит от обозначения переменной интегрирования.
Переменную
интегрирования можно обозначить в
принципе любой буквой. Тогда справедливы
равенства:
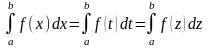 (2)
(2)
Заменив это,
рассмотрим определенный интеграл
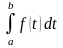 с
нижним пределом а
и верхним пределом х,
где
с
нижним пределом а
и верхним пределом х,
где
 ,
причем переменную интегрирования мы
обозначаем буквой t
в отличие
от верхнего предела
,
причем переменную интегрирования мы
обозначаем буквой t
в отличие
от верхнего предела
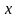 .
Каждому значению
отрезка
соответствует одно определенное число
.
Каждому значению
отрезка
соответствует одно определенное число
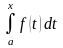 .
.
Тогда, рассматриваемый интеграл
представляет собой на
некоторую
функцию верхнего предела
.
Обозначим эту функциючерез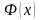 :
: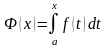 2’)
2’)
Относительно этой функции докажем следующую теорему.
Теорема 2.1: Если -непрерывная на функция и , то имеет место равенство:
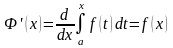 (2.1)
(2.1)
Другими
словами, производная от интеграла (1) по
его переменному верхнему пределу равна
значению подынтегральной функции
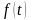 при
при
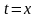 (при
условии, что подынтегральная функция
непрерывна).
(при
условии, что подынтегральная функция
непрерывна).
Доказательство:
Придадим
аргументу x
приращение
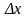 (так чтобы значение
(так чтобы значение
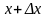 принадлежало
).
Тогда новое значение функции (2’) будет:
принадлежало
).
Тогда новое значение функции (2’) будет:
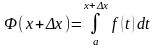 .
Или по свойству 1.4.4:
.
Или по свойству 1.4.4:
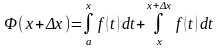 .
Найдем приращение функции
:
.
Найдем приращение функции
:
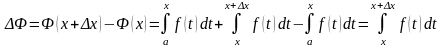 К этому интегралу применим теорему о
среднем значении (свойство 1.4.7):
К этому интегралу применим теорему о
среднем значении (свойство 1.4.7):
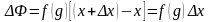 ,
где
заключено между
и
.
,
где
заключено между
и
.
Найдем
 .
По определению производной,
.
По определению производной,
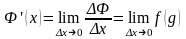 .
.
Но
если
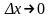 ,
то
,
то
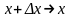 ,
поэтому и
,
поэтому и
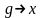 .
В силу непрерывности функции
(что
дано по условию)
.
В силу непрерывности функции
(что
дано по условию)
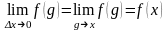
Итак,
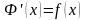 ,
что и требовалось доказать.
,
что и требовалось доказать.
Из доказанной теоремы следуют такие теоремы:
Теорема 2.2: Если функция непрерывна на , то функция , , является первообразной для функции на этом отрезке.
Выше мы доказали, что , а это и означает, что есть первообразная функция для .
Теорема 2.3: Всякая непрерывная на функция имеет на нем первообразную. (об этом говорилось в разделе «Неопределенные интегралы»)
Доказано, примером первообразной функции для является, как мы только что видели, функция .
Теоремы 1 и 2 имеют важное значение в интегральном исчислении.
3. Формула Ньютона-Лейбница.
(основная формула интегрального исчисления)
Теорема
3,1: Если
функция
непрерывна
на отрезке
и
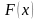 есть какая-либо первообразная для
на
этом отрезке, то справедлива следующая
формула:
есть какая-либо первообразная для
на
этом отрезке, то справедлива следующая
формула:
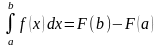 (*)
(*)
Доказательство:
По условию является первообразной для функции на .
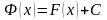 (3.1)
(3.1)
Где
С – некоторая постоянная. Для отыскания
С положим в тождестве (1)
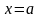 .
Замечая, что при этом
.
Замечая, что при этом
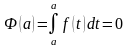 ,
получим :
,
получим :
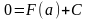 ,
откуда
,
откуда
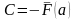 ,
и, след.,
,
и, след.,
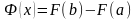 (3.1’)
(3.1’)
или
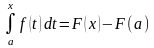 ,
или, изменив обозначение переменной
интегрирования с t
на x,
будем иметь:
,
или, изменив обозначение переменной
интегрирования с t
на x,
будем иметь:
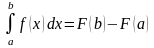 - Эта формула является основной в
интегральном исчислении; её обычно
называют формулой Ньютона-Лейбница.
- Эта формула является основной в
интегральном исчислении; её обычно
называют формулой Ньютона-Лейбница.
Формула Ньютона-Лейбница выражает следующий весьма важный факт: Определенный интеграл на от непрерывной на этом отрезке функции равен разности значений любой первообразной функции для , вычисленных при верхнем и нижнем пределах b и a интеграла.
Эта формула сводит вычисление определенного интеграла к определению какой-либо первообразной для подынтегральной функции . Тем самым вычисление определенного интеграла от непрерывной функции сводится формулой (*) к вычислению соответствующего неопределенного интеграла
Итак, чтобы вычислить определенный интеграл от непрерывной на функции достаточно:
1).
Вычислить неопределенный интеграл от
на
:
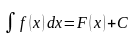 ,
и положив С, например, равным нулю,
получить одну из первообразных функций
для
на
.
,
и положив С, например, равным нулю,
получить одну из первообразных функций
для
на
.
2).
Вычислить
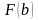 и
и
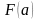 ,
т.е. значения функции
при верхнем пределе
,
т.е. значения функции
при верхнем пределе
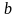 и нижнем пределе
и нижнем пределе
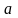 интеграла, и из первого результата
вычесть второй.
интеграла, и из первого результата
вычесть второй.
Формула Ньютона-Лейбница даёт эффективное и простое средство для вычисления определенного интеграла от непрерывной функции . Ведь для ряда простых классов таких функций мы умеем выражать первообразную в конечном виде через элементарные функции. В этих случаях определенный интеграл вычисляется непосредственно по основной формуле.
Во всех тех случаях, когда возможно найти для непрерывной функции первообразную, выраженную в конечном виде через элементарные функции, можно без особого труда вычислить определенный интеграл по формуле (*).
Только с открытием этой формулы определенный интеграл смог получить то значение в математике, какое он имеет в настоящие время. С открытием этой формулы математика получила общий метод для решения различных задач частного вида и поэтому смогла значительно расширить круг приложений определенного интеграла к технике, механике, астрономии и т.д.
Приращение
первообразной
,
полученное ею при переходе аргумента
от значения
к значению
,
т.е. разность
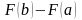 ,
часто обозначается так:
,
часто обозначается так:
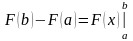 ,
где символ
,
где символ
 называют
знаком двойной подстановки, саму операцию
вычисления разности
называют выполнением двойной подстановки
относительно функции
(с пределами
и
).
называют
знаком двойной подстановки, саму операцию
вычисления разности
называют выполнением двойной подстановки
относительно функции
(с пределами
и
).
Читается символ двойной подстановки следующим образом: “подстановка от до для функции ”
Пользуясь введённым
обозначением, формулу Ньютона-Лейбница
можно переписать в следующем виде:
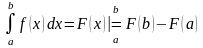
Применим формулу Ньютона-Лейбница к вычислению нескольких определенных интегралов.
Пример
3.1.1: Вычислить
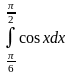
Т.к.
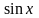 есть первообразная функция для непрерывной
функции
есть первообразная функция для непрерывной
функции
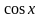 ,
то по формуле (*) получаем:
=
,
то по формуле (*) получаем:
=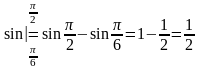 .
.
Пример
3.1.2: Вычислить
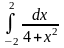
Сначала находим соответствующий неопределенный интеграл, а затем применяем формулу (*):
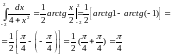
При вычислении определенных интегралов по формуле Ньютона-Лейбница надо строго следить за тем, чтобы выполнялись все условия, при которых была выведена эта формула, иначе может получиться неправильный результат.
Применение формулы
Ньютона-Лейбница для вычисления
определенного интеграла от непрерывной
на
функции
предполагает выполнение равенства
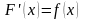 на
всем отрезке
интегрирования. Отсюда, в частности,
следует непрерывность функции
на этом отрезке.
на
всем отрезке
интегрирования. Отсюда, в частности,
следует непрерывность функции
на этом отрезке.
Нарушение непрерывности хотя бы в одной точке отрезка (конечно, в этой точке уже не будет иметь смысла равенство ) может привести к ошибочному результату.
* * *
Очевидно, все методы вычисления неопределенных интегралов могут быть непосредственно применены и к вычислению определенных интегралов; при этом сами вычисления во многих случаях значительно упрощаются по сравнению с вычислениями, производными непосредственно (по формуле Ньютона-Лейбница).
Рассмотрим теперь вопрос о применении метода подстановки и метода интегрирования по частям к вычислению определенных интегралов.
