Площадь криволинейной трапеции.
-
Площадь криволинейной трапеции.
Замечание: Мы рассмотрели задачу из геометрии и из механики - две совершенно различные по своему содержанию задачи. К вычислению пределов подобного вида приводит решение и других, не менее важных задач математики, физики техники и иных областей знания.
Поэтому возникает необходимость изучить подобные суммы в общем виде, отвлекаясь от конкретного смысла входящих в них переменных величин, и установить удобные на практике примеры вычисления пределов этих сумм.
1.2. Понятие определенного интеграла.
Пусть на [a;b] задана непрерывная функция y=f(x).
1) Разобьем отрезок [a;b] на п частичных отрезков с помощью произвольно выбранных на нем точек :
2) На каждом из
частичных отрезков возьмём произвольную
точку
(I=1,2,…,n).
Во взятых точках вычислим значения
функции
3) Составим
произведения длин
частичных
отрезков на значения функции
4)Все эти произведения
сложим и сумму их обозначим через
:
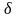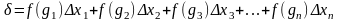или
(1.2.1)
Сумму такого вида называют интегральной суммой, составленной для функции f(x) на отрезке [a;b].
Будем неограниченно
увеличивать число делений отрезка
[a;b],
однако так, чтобы длина
каждого отрезка
стремилась
к нулю и рассмотрим получающиеся при
этом множество интегральных сумм
.
Если при этом
разбиении суммы
будут
стремится к одному и тому же пределу
,
то этот предел называют определённым
интегралом от функции f(x)
на отрезке
[a;b].
Обозначают его с помощью символа
Определение 1.2.1: Если существует предел J суммы (1).При , то говорят, что функция f(x) интегрируема на [a;b], а число J называют определённым интегралом от функции f(x) на [a;b].
По определению,
(1.2.2)
Числа “a” и ”b” называются пределами интегрирования (или интеграла), соответственно нижним и верхним; отрезок [a;b]-промежутком интегрирования.
Таким образом – определённый интеграл есть предел множества интегральных сумм.
N-ного способа введения определённого интеграла означает, что величина его зависит только от подитегральной функции f(x) и пределов a и b интеграла.
По своему обозначению определённый интеграл назначает неопределённый. По существу это- различные понятия:
неопределенный интеграл - это некоторое множество функций от переменой интегрирования;
определенный – при постоянных a и b представляет собой число и след., никак не зависит от переменной интегрирования.
В дальнейшем, однако, будет установлена тесная связь между этими интегралами. (станет ясной сходность обозначений).
Возвращаясь теперь
к задачам, рассмотренным выше и применяя
введённое понятие определенного
интеграла, мы можем записать, что площадь
криволинейной трапеции
(1.2.3) геометрический смысл
определённого интеграла и что
.
(1.2.4)
Необходимое условие интегрируемости функций.
Легко видеть, что функция f(x) может быть интегрируемой на отрезке только тогда, когда она ограничена на нем.
Доказано, если функция f(x) на отрезке [a;b]была бы не ограничена то при любом разбиении отрезка на части – она сохранила бы подобное свойство хоть в одной из частей. Тогда(за счет выбора в этой части точки g) можно было бы сделать f(g), а с ней и сумму ,- сколь угодно большой; при этих условиях интегральная сумма не будет иметь предела.
Таким образом – функция, интегрируемая на данном отрезке, необходимо ограничена на нем, это условие, однако, не является достаточным для интегрируемости функции.