
- •1 Определённый интеграл
- •1. Задачи, приводящие к понятию определённого интеграла.
- •Площадь криволинейной трапеции.
- •1.2. Понятие определенного интеграла.
- •1.3. Теорема существования определенного интеграла (без доказательства).
- •1.4. Основные свойства определенного интеграла.
- •2.Произвольная от определённого интеграла по переменному верхнему пределу.
- •3. Формула Ньютона-Лейбница.
- •4. Интегрирование по частям в определенном интеграле.
- •5. Несобственные интегралы
- •5.2 Несобственные интегралы от разрывных функций
- •5.3Интегралы, зависящие от параметра. Рассмотрим интеграл вида
- •Бета-функция.
- •Приложения определенного интеграла.
- •6. Геометрические приложения определенных интегралов.
- •6.1. Вычисление площадей плоских фигур.
- •6.2. Длина дуги.
- •6.3.Вычисление объёмов тел вращения.
- •6.4. Вычисление объемов тел по известным поперечным сечениям
- •6.5.Площадь поверхности вращения.
- •7. Приложения определенных интегралов к решению задач физики.
- •7.1.Путь пройденный телом
- •7.2.Работа силы
- •7.3. Количество электричества.
- •7.4. Вычисление давления
- •7.5. Кинематическая энергия
- •7.6. Статический момент.
- •7.7.Координаты центра тяжести.
- •8.Тестовые задания для самостоятельной работы.
- •9. Физические задачи для самостоятельной работы
- •10. Приближенные методы вычисления определенных интегралов.
- •450062, Республика Башкортостан, г. Уфа, ул. Космонавтов,1
7.2.Работа силы
Пусть материальная точка движется вдоль оси Ох от точки х=а, до х=b (а<b) под действием переменной силы F=F(x),причём направление силы совпадает с направлением движения. Найти работу, произведенную силой на этом перемещение. Возьмём элементарное перемещение [x,x+dx].Работа силы на этом перемещение
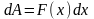
Мы получим «элемент» работы. Теперь проинтегрируем по отрезку[a,b] и получим искомую работу:
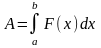
7.2.1. Тело
движется по прямой
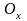 из
точки с абсциссой a
до
точки с абсциссой b(a<b)
под
действием переменной
силы
из
точки с абсциссой a
до
точки с абсциссой b(a<b)
под
действием переменной
силы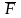 ,
являющейся
непрерывной функцией абсциссы х:
=
(х),
причем
сила параллельна прямой
,
а
ее направление совпадает с направлением
движения тела. Найти работу
A,
произведенную
силой
(х)на
этом перемещении.
,
являющейся
непрерывной функцией абсциссы х:
=
(х),
причем
сила параллельна прямой
,
а
ее направление совпадает с направлением
движения тела. Найти работу
A,
произведенную
силой
(х)на
этом перемещении.
Решение. Если бы сила (х) была не переменной, а постоянной, параллельной прямой Ох, и ее направление совпадало с направлением движения тела, то работа A, произведенная ею, была бы равна произведению модуля силы на пройденный путь, т. е. на длину отрезка [а,b], равную (b—а):
A = F(b— а).
Но сила переменна, а потому этой формулой для определения работы мы воспользоваться не можем.
Отрезок
[а,b]
разделим
на п
отрезков
[xk-1
xk]
(k=l,2,3,
...,n).
На
каждом из них выберем произвольную
точку
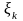 .
Определим
в этой точке численное значение силы
(х)
Получится
число
(
).
Полагая,
что в пределах каждого частичного
отрезка сила не переменна, а постоянна
и что ее значение на всем частичном
отрезке такое же, как в выбранной точке,
будем считать произведенную этой силой
работу приближенно на каждом частичном
отрезке равной произведению модуля
силы на путь, т. е.
(
)∆xk
.
Определим
в этой точке численное значение силы
(х)
Получится
число
(
).
Полагая,
что в пределах каждого частичного
отрезка сила не переменна, а постоянна
и что ее значение на всем частичном
отрезке такое же, как в выбранной точке,
будем считать произведенную этой силой
работу приближенно на каждом частичном
отрезке равной произведению модуля
силы на путь, т. е.
(
)∆xk
Работа силы (х) на всем отрезке [а, b] приближенно равна сумме работ на всех частичных участках
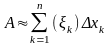
Сумма
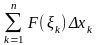 —
интегральная сумма для функции F(x).
на
отрезке [а,b].
По
формуле (11,4) мы получим не точное значение
работы, а приближенное, потому что на
каждом частичном отрезке мы считали
силу постоянной, в то время как фактически
в пределах каждого частичного отрезка
она непрерывно изменяется.
—
интегральная сумма для функции F(x).
на
отрезке [а,b].
По
формуле (11,4) мы получим не точное значение
работы, а приближенное, потому что на
каждом частичном отрезке мы считали
силу постоянной, в то время как фактически
в пределах каждого частичного отрезка
она непрерывно изменяется.
За
точное значение работы силы
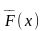 на отрезке [а,b]
мы
примем тот предел, к которому стремится
интегральная сумма (11,4), когда наибольший
из частичных отрезков ∆xk
стремится
к нулю, а число их n
неограниченно
возрастает, т. е.
на отрезке [а,b]
мы
примем тот предел, к которому стремится
интегральная сумма (11,4), когда наибольший
из частичных отрезков ∆xk
стремится
к нулю, а число их n
неограниченно
возрастает, т. е.
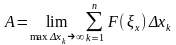
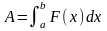 (11.5)
(11.5)
Подынтегральное выражение F(х)dx называется элементарной работой и обозначается через δА
Работа А есть определенный интеграл от элементарной работы δА= F(х)dx. Таким образом, для определения работы переменной силы на прямолинейном пути надо сначала вычислить элементарную работу δА, а после этого интегрированием по формуле (11,5) найти полную работу.
Приближенное значение работы, вычисленное по формуле (11,4), будет тем меньше отличаться от ее точного значения (11,5), чем меньшими будут частичные отрезки ∆xk, на которые разбит отрезок [а,b] .
При определении предела суммы (11,4) наибольший из отрезков ∆xk→0, каждое слагаемое ( )∆xk — величина бесконечно малая, а количество их неограниченно возрастает. Поэтому и здесь определение искомой величины, как и в задаче 11,1 связано с определением предела суммы бесконечно малых величин, когда их количество неограниченно возрастает.
7.2.2. Какую работу надо совершить, чтобы растянуть пружину на 4 см, если известно, что от нагрузки 1 Н она растягивает на 1 см?
Решение.
Согласно
закону Гука сила F
Н, растягивающая пружину на х
м, равна
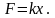 .Коэффициент
пропорциональности
найдём из условия :
.Коэффициент
пропорциональности
найдём из условия :
Если х=0,01м, то F=1Н;
Следовательно,
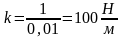 и
и
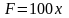 .Тогда
.Тогда
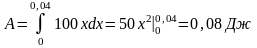
7.2.3.Растяжения пружины на 0,04 м необходимо совершить работу 20 Дж. На какую длину модно растянуть пружину, совершить работу в 80 Дж?
Решение.
По длине растяжения пружины на 0,04м и совершенной работе 20 Дж найдём:
k:
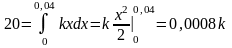 ,
,
Откуда
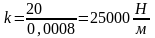
По
и
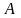 найдем
:
найдем
:
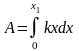
где -длина, на которую растянута пружина при совершенной работе в 80 Дж.
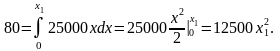
Откуда
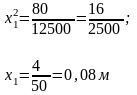
7.2.4.Ккаую работу нужно затратить, чтобы тело массы m поднять с поверхности Земли на высоту h?Чему равна эта работа, если тело должно быть удалено на бесконечность?
Решение. Величина сила F ,производящей работу при поднятие тела с поверхности земли, равна величине сила притяжения тела Земли, т.е.
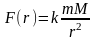 ,
,
где
m-масса
тела,M-масса
Земли,r-расстояние
от тела до центра Земли. В этом же
направлении происходит и перемещение
тела из положения
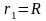 (R-радиус
Земли) в положение
(R-радиус
Земли) в положение
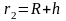 .Работу
силы F(r)
на пути [R,R+h]
вычислим с помощью интеграла
.Работу
силы F(r)
на пути [R,R+h]
вычислим с помощью интеграла
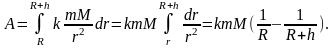
Учитывая,
что на поверхности Земли(при
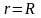 )
сила притяжения
)
сила притяжения
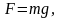 найдём
коэффициент
:
найдём
коэффициент
:
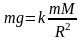 откуда
откуда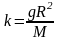
Тогда
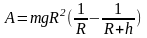 и
и
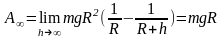
7.2.5.Вычислить работу, которую надо совершить, чтобы выкачать воду из резервуара конической формы с вершиной, обращенной к низу. Резервуар наполнен доверху водой. Радиус основания конуса R=1, высота конуса 2м.
Решение. На глубине х выделяем горизонтальный слой высоты dx
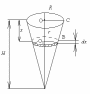
Элементарный слой принимаем за цилиндр ввиду малости dx.Тогда
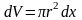
Выразим r-радиус слоя через х и постоянные R и H. Из подобия треугольников АОС и АО1В имеем:
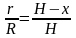 откуда
откуда
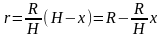
Далее получим
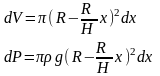
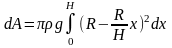
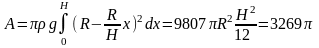 Дж
Дж
7.2.6.
Шар лежит на дне бассейна глубиной
Н=14мюОпределить работу, необходимую
для извлечения шара из воды, если его
радиус R=3дм,а
удельный вес
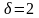 .
.
Решение.
При подъеме шара до поверхности воды сила P1 совершающая работу, постоянна и равна разносим между весом шара и весом вытесняемой им воды:
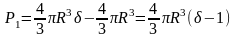
Поэтому работа Q1, необходимая для поднятия шара до поверхности воды, определяется как произведение силы P1 на высоту подъема H-2R:
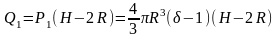
При дальнейшем подъеме шара сила p,совершающая работу, будет изменяться в зависимости от высоты х надводной части шара
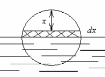
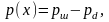
где
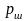 -вес
шара ,
-вес
шара ,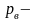 вес
воды, вытесняемой подводной частью
шара, численно равный объему шарового
сечения с высотой
вес
воды, вытесняемой подводной частью
шара, численно равный объему шарового
сечения с высотой
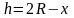 ;
;
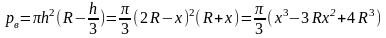
Очевидно, и работа, совершаемая силой p(x), некоторой функцией g(x).Допуская, что при подъёме шара ещё на малую высоту dx сила p(x) остается неизменной, найдем приближенную величину приращения работы.
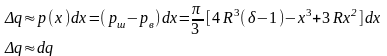
Интегрируя
dq
в пределах от x=0
до x=2R
найдем работу
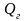 ,которою
надо совершить, чтобы шар, поднятый со
дна бассейна до поверхподнятой воды,
полностью извлечь из воды:
,которою
надо совершить, чтобы шар, поднятый со
дна бассейна до поверхподнятой воды,
полностью извлечь из воды:
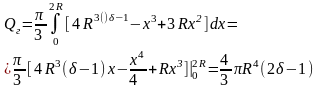
Вся искомая работа
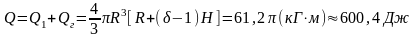
7.2.7. Какую работу затрачивает подъемный кран при извлечении железобетонной надолбы со дна реки глубиной в 5 м, если надолба имеет форму правильного тетраэдра с ребром 1м,а плотность железобетона 2500 кг/м3
Решение.
Высота
тетраэдра
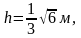 объем тетраэдра
объем тетраэдра
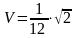 м3.Вес
надолбы в воде
м3.Вес
надолбы в воде
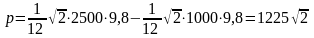 Н,
Н,
Поэтому работа на извлечение надолбы до момента появления на поверхности воды её вершины
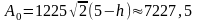 Дж
Дж
Теперь найдем работу А1 на извлечение надолбы из воды. Пусть вершина тетраэдра вышла на высоту 5+у,
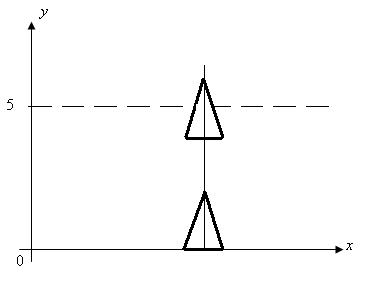
Тогда
объем малого тетраэдра, вышедшего из
воды, равен
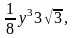 а вест тетраэдра
а вест тетраэдра
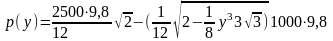 Н
Н
Следовательно
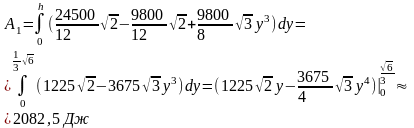
7.2.8. (работа упругой силы на прямолинейном перемещении).
К телу прикреплена пружина, другой конец которой закреплен неподвижно в точке О. Упругая сила, с которой действует пружина на тело, подчиняется закону Гука, согласно которому F=—kx, где k—коэффициент пропорциональности, а х — удлинение пружины. Найти работу упругой силы на прямолинейном перемещении по линии действия силы из точки с абсциссой a в точку с абсциссой b. (Сила — в килограммах, перемещение — в метрах). Знак минус в выражении силы показывает, что упругая сила стремится восстановить равновесие.
Решение. Элементарная работа δА силы упругости на перемещении dx равна
dA=—kx dx,
а потому полная работа на перемещении из точки а в точку b определится по формуле
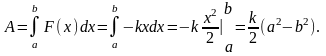
Следует иметь в виду, что работа упругой силы положительна, если тело движется в сторону убывания модуля упругой силы, и отрицательна, когда движение происходит в сторону возрастания модуля упругой силы.
7.2.9. Тяжелая цепь длиною L = 200 м поднимается, навиваясь на ворот. Определить работу силы веса при поднятии цепи, пренебрегая размерами ворота, если погонный метр цепи весит 50 кг.
Решение. Пусть к некоторому моменту времени на ворот навернулся отрезок цепи длиной х. Тогда свешивается его часть длиной L—х. Весит эта часть (L—х)•50кг. Элементарная работа силы веса на перемещении dx будет равна
δА=—(L—х)∙50dx.
(Знак минус поставлен потому, что сила веса направлена противоположно перемещению). Полную работу найдем по формуле (11,5) как интеграл от элементарной работы
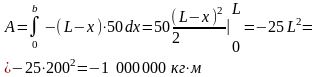
7.2.10. Вычислить работу, необходимую для выкачивания масла из вертикального цилиндрического резервуара высотой H = 6м и радиусом основания R = 2 м. Удельный вес масла δ = 0,9.
Решение. Величина работы q, затрачиваемой на поднятие некоторого тела, зависит от высоты х его подъема: q=Px, Р— вес тела.
Допустим, что работа, затраченная на выкачивание из резервуара слоя масла толщиною х, черт. 1 , есть некоторая функция q (x) и найдем дифференциал этой функции. При увеличении х на величину dx объем v слоя масла увеличится на величину ∆υ = π R2dx, его вес р увеличится на вели-
Черт.
I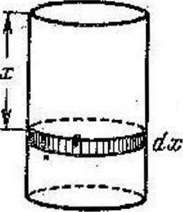
чину ∆p=πδR2dx, а затраченная работа q увеличится на величин у ∆q ≈ πδR2 х dx = dq.
Всю искомую работу Q получим при изменении х от 0 до H. Поэтому
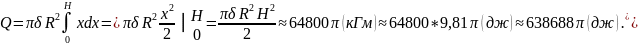
7.2.11. Цилиндр высотой Н= 1,5 м и радиусом R = 0,4м, наполненный газом под атмосферным давлением (10330кГ/м2), закрыт поршнем. Определить работу, затрачиваемую на изотермическое сжатие газа при перемещении поршня на расстояние h = 1,2 м внутрь цилиндра.
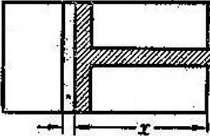
Решение. При изотермическом изменении состояния газа, когда его температура остается неизменной, зависимость между объемом υ и давлением р газа выражается
формулой pυ= с = const.(Закон Бойля-Мариотта)
Поэтому, если поршень будет вдвинут на х м внутрь цилиндра (черт: 1 '), то давление р(х) газа на единицу площади поршня будет
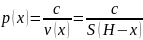
Полагая, что работа, затрачиваемая при вдвижении поршня на х м, есть некоторая функция q{x), .и допуская, что при дальнейшем вдвижении поршня. на малое расстояние dx испытываемое им давление Р(х) остается неизменным, найдем, приближенную величину приращения (дифференциал) функции q(x):
∆q
≈ Р (х)dx
=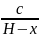 dx
= dq.
dx
= dq.
Всей искомой работе Q соответствует .изменение х от 0 до h, поэтому
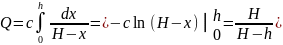
При
H=1,5м,
R = 0,4м,
h ~=
1,2
м,
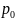 = 10 330
кГ/м2
найдем
v0
=
πR2H=0,24πм3;
c = p0v0
= 2479,2π;
Q ≈ 12533,3
кГм
≈122951,7
дж.
= 10 330
кГ/м2
найдем
v0
=
πR2H=0,24πм3;
c = p0v0
= 2479,2π;
Q ≈ 12533,3
кГм
≈122951,7
дж.
7.2.12. Сжатие S винтовой пружины пропорционально приложенной силе F. Вычислить работу силы F при сжатии пружины на 5 см, если для сжатия её на 1 см нужна сила в 1 кг (Рис. 245).
Р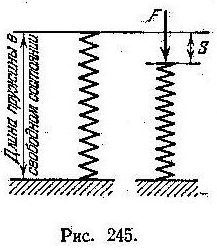 ешение.
Сила F
и перемещение
S
связаны
по условию зависимостью F
= kS,
где k
– постоянная.
ешение.
Сила F
и перемещение
S
связаны
по условию зависимостью F
= kS,
где k
– постоянная.
Будем выражать S в метрах, F – в килограммах. При S = 0.01 F = 1, т. е.
1 = k · 0.01, откуда k = 100, F = 100S.
На основе формулы (1) имеем:
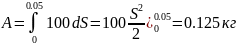
7.2.13. Сила F, с которой электрический заряд e1 отталкивает заряд e2 (того же знака), находящийся от него на расстоянии r, выражается формулой
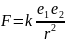 ,
,
где k – постоянная.
Определить работу силы F при перемещении заряда e2 из точки A, отстоящий от заряда e1 на расстоянии r1 в точку A2, отстоящую от e1 на расстоянии r2, полагая, что заряд e1 помещен в точке A0, принятой за начало отсчета.
Решение. По формуле (1) имеем:
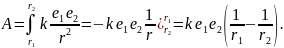
При r2 = ∞ получим:
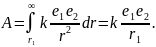
При e2
= 1
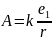 .
Последняя величина называется потенциалом
поля,
создаваемого зарядом e1.
.
Последняя величина называется потенциалом
поля,
создаваемого зарядом e1.
