7. Приложения определенных интегралов к решению задач физики.

7.1.Путь пройденный телом

Путь, пройденный телом, при неравномерном движение со стороны υ=f(t),за промежуток времени [t₁;t₂], равен

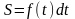
7.1.1.Два тела начали двигаться в один и тот же момент из одной точки в одном направление по прямой. Одно тело двигалось со скоростью 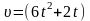м/сек, другое со скоростью 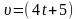м/с.На каком расстояние они будут друг от друга через 5 сек?

Решение. По формуле вычислим пройденный путь первым и вторым телом:

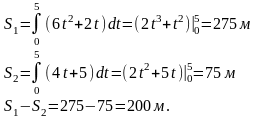
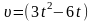7.1.2.Два тела движутся по прямой из одной и той же точки. Первое тело движется со скоростью м/с, второе –со скоростью 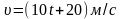.В какой момент и на каком расстояние от начальной точки произойдёт их встреча?

Решение. В условие задачи дано, что тела начали двигаться из одной и той же точки, поэтому их пути дол встречи будут равны. Найдём уравнение пути каждого из тел

Постоянные интегрирования без начальных условиях: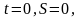 будут равны нулю. Встреча этих тел произойдёт при 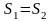,откуда

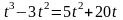или

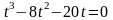
Решим это уравнение

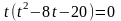
Откуда

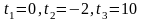
В момент 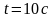произойдёт встреча этих тел после начла движения .Из уравнений пути находим

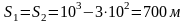
7.1.3. Тело брошено с поверхности земли вертикально вверх со скоростью .Найти наибольшую высоту подъема тела.

Решение. Тело достигнет наибольшей высоты подъема в момент t,когда υ=0,т.е.

39,2-9,8t=0 откуда t=4 сек

Находим

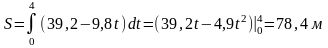
7.1.4. Материальная точка движется по прямой с переменной ско­ростью, являющейся заданной непрерывной функцией времени t: v = v (t). Определить путь, пройденный телом от момента вре­мени t₀ до момента Т.

Указание. Промежуток времени [t₀, Т] разделить на n произвольных частей. Длина каждого промежутка времени

∆t_k = t_k - t_k-1 .

В каждом частичном промежутке времени выберем произволь­ный момент — τ_k. (Момент τ_k может совпадать и с любым из концов отрезка времени ∆τ_k).

Вычислим скорость v в этот момент времени. Получится число f(τ_k)Принимаем, что за время ∆τ_k движение происходит равномерно. Поскольку при равномерном прямолинейном движении путь, прой­денный телом, равен произведению скорости на время, путь, прой­денный за время ∆τ_k, будет приближенно равен f(τ_k)∆τ_k. Сложим пути, пройденные за все частичные отрезки времени.

Приближенное значение пути

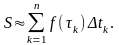(11,10)

За точное значение пути S следует принять предел интеграль­ной суммы (11,10), когда наибольший из промежутков времени ∆t_k стремится к нулю:

На основании формулы (10,2) можно записать, что

т

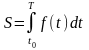(11,11)

Таким образом, если задан закон изменения скорости, то путь, пройденный телом, вычисляется с помощью определенного инте­грала по формуле (11,11).

Когда max ∆t_k→0, то произведение v(τ_k)∆τ_k — величина беско­нечно малая. Определение искомой величины и в этой задаче свелось к отысканию предела суммы неограниченно возрастающего количества бесконечно малых величин.

7.1.5. Вычислить путь, пройденный свободно падающим в пустоте телом за Т секунд, если известно, что скорость v свободного па­дения в пустоте определяется формулой v = gt (начальную ско­рость v₀ принимаем равной нулю).

Ответ. 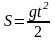. Если v₀≠0 то v=v₀+gt, a