Задача №3

Непрерывная случайная величина.

Вариант 1. Функция распределения случайной величины определяется следующим образом:

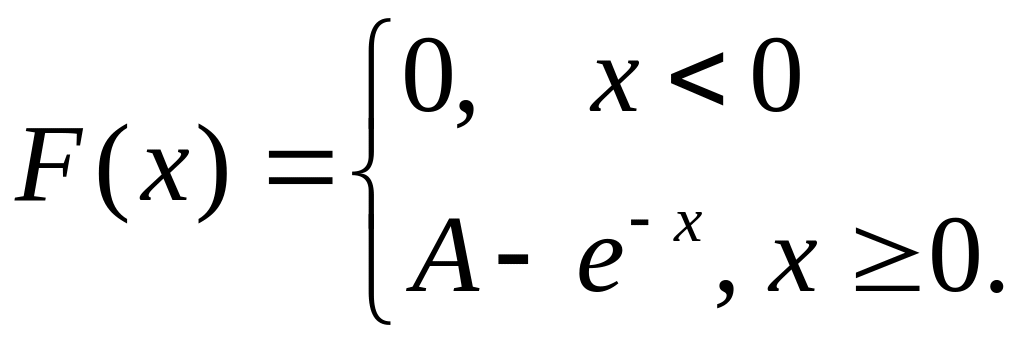
Определить , плотность вероятности, , и .

Вариант 2. Известно, что:

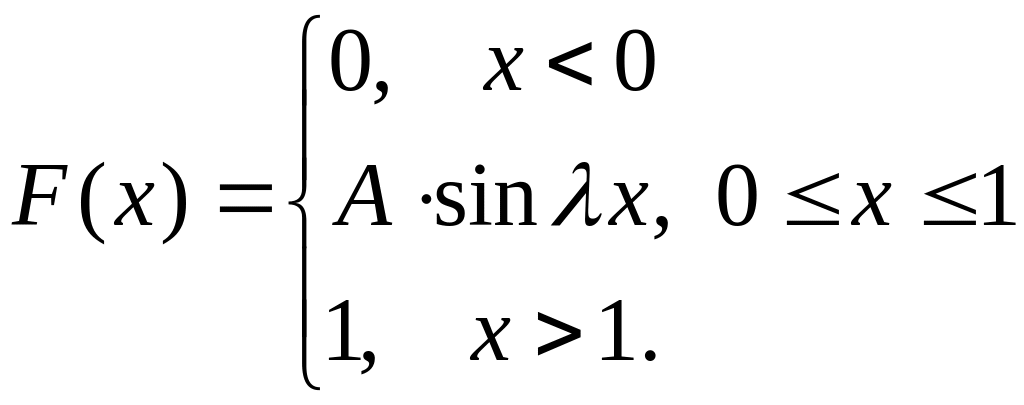
Определить в этих условиях , , плотность вероятности, , и .

Вариант 3. Пусть:

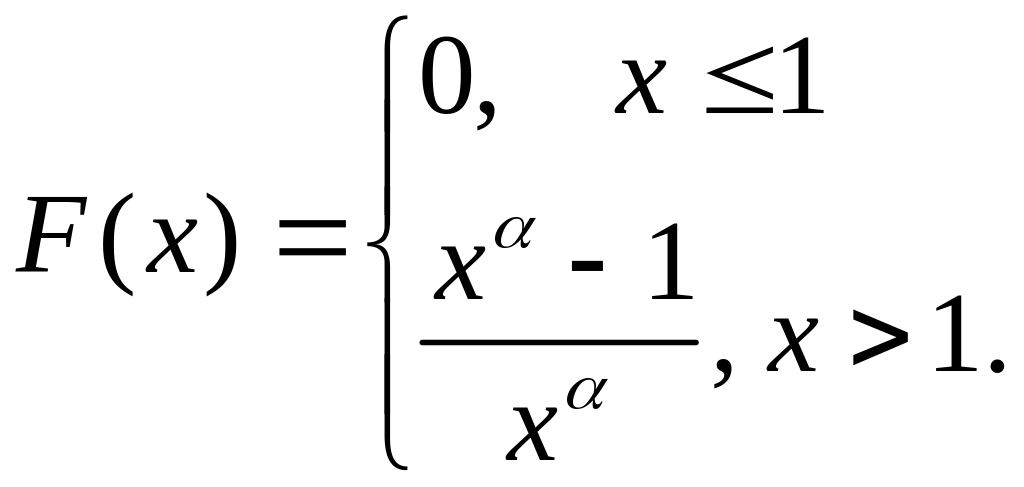
При каком значении дисперсия этой случайной величины будет конечной?

Вариант 4. Случайная величина имеет плотность вероятности . Определить , , и .

Вариант 5. Функция распределения случайной величины задаётся формулами:

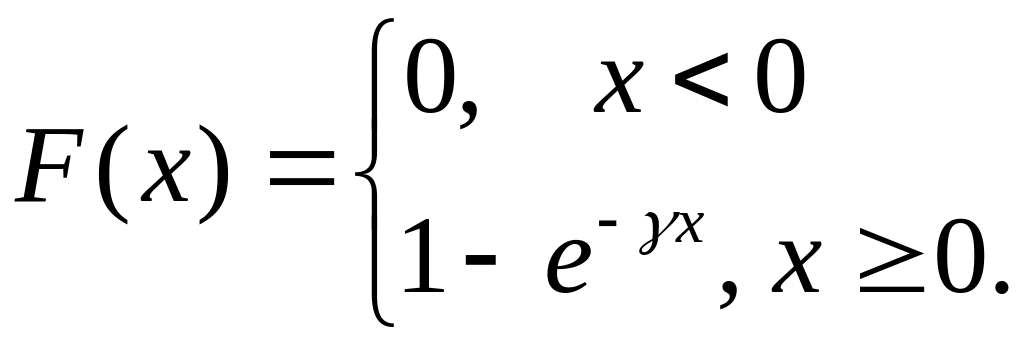
При каком значении дисперсия этой величины будет меньше 1?

Вариант 6. Функция распределения случайной величины имеет вид:

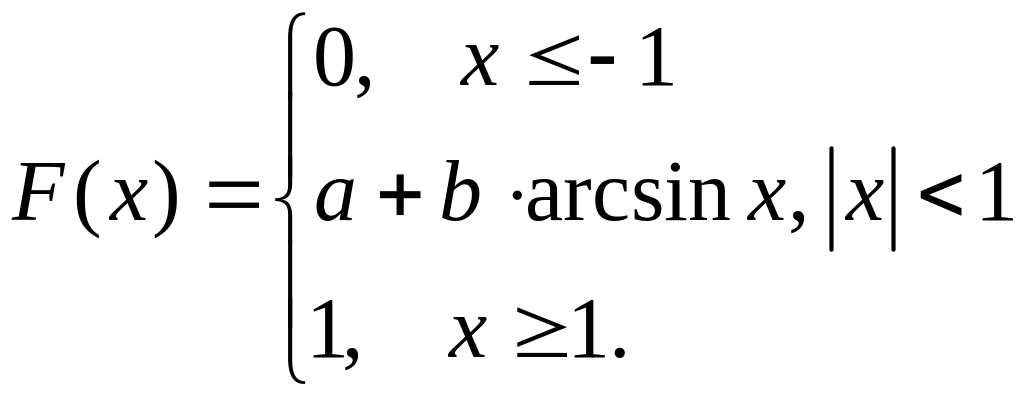
Определить и , найти , , и .

Вариант 7. Функция распределения случайной величины определяется по формуле: 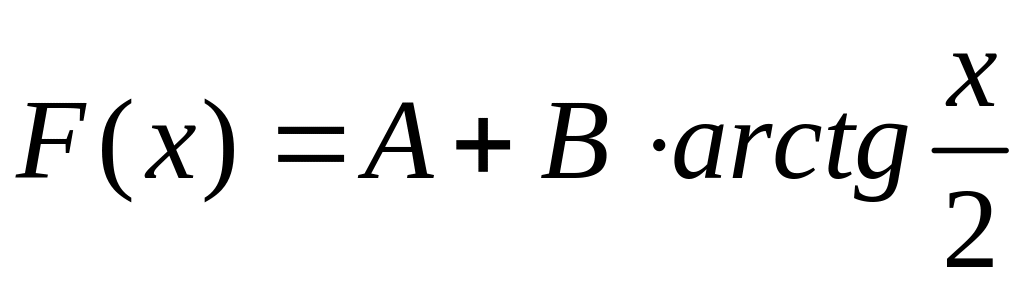. Определить постоянные и . Найти ?

Вариант 8. Плотность вероятности . Определить , , , и .

Вариант 9. Плотность вероятности . Определить , , , и .

Вариант 10. Плотность вероятности при , при . Определить , , и .

Вариант 11. Дана функция распределения случайной величины :

Определить значение постоянной из условия непрерывности , а также плотность вероятности, , и .

Вариант 12. Дана плотность вероятности . Определить значение постоянной , найти функцию распределения , а также , и .

Вариант 13. Дана плотность вероятности:

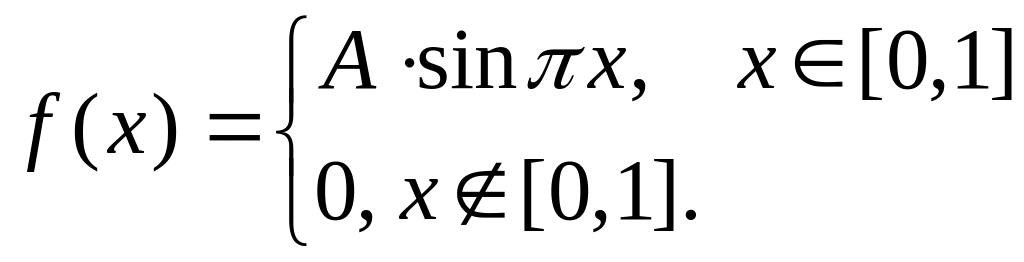
Определить функцию распределения , , , и .

Вариант 14. Пусть  – равномерная на отрезке случайна величина. Будет ли величина также равномерной? Какова её плотность вероятности?

Вариант 15. Известно, что  – равномерная случайная величина на отрезке . Найти функцию распределения величины . Определить плотность вероятности и .

Вариант 16. Пусть  – стандартная нормальная величина. Определить отрезок единичной длины, вероятность попадания в который наибольшая.

Вариант 17. Известно, что плотность вероятности величины равна 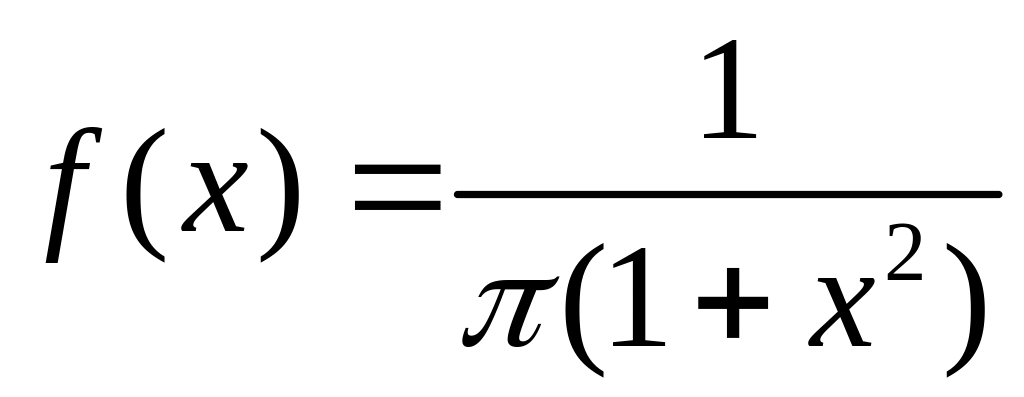. Определить отрезок единичной длины с наибольшей вероятностью попадания.

Вариант 18. Функция распределения некоторой случайной величины задана:

Определить симметричный относительно интервал вероятность попадания в который равна 0,99.

Вариант 19. Величина имеет равномерное распределение на отрезке . Найти функцию распределения и плотность вероятности величины .

Вариант 20. Случайная величина задана своей функцией распределения:

Определить все интервалы длиной 0,25 вероятность попадания в которые не менее 0,7.

Вариант 21. Даны две случайные величины и , имеющие плотности вероятности:

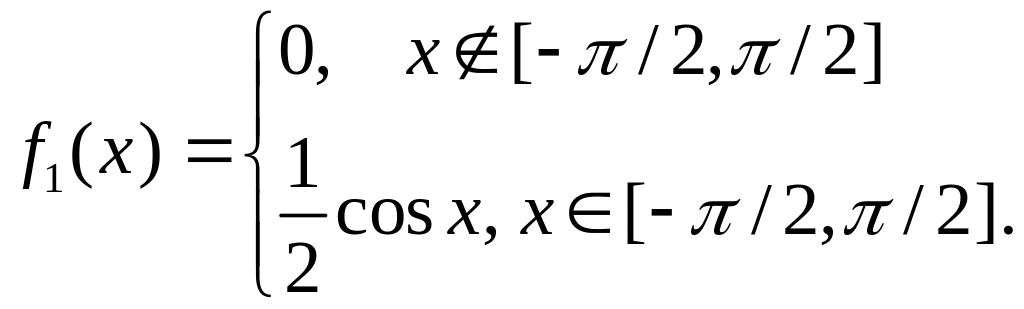
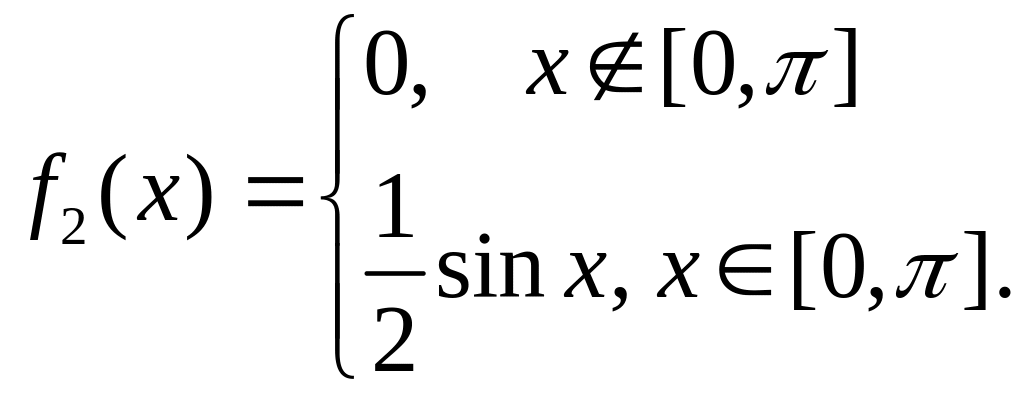
Определить третью величину с плотностью , таким образом, чтобы была минимальной.

Вариант 22. Величина имеет равномерное распределение на отрезке , а величина равномерна на . Определить величину с плотностью вероятности , так, чтобы была минимальной, где ,  – плотности вероятности величин и .

Вариант 23. Известно, что . Найти отрезок длиной 2, вероятность попадания в который максимальна.

Вариант 24. Пусть . Определить отрезок единичной длины, вероятность попадания в который максимальна.

Вариант 25. Экспериментальные исследования показали, что плотность вероятности некоторой случайной величины может быть выражена формулами:

Выбрать постоянные , из условия .

Вариант 26. Известно, что , при этом . Определить в этих условиях .

Вариант 27. Случайная величина . Известно, что . Чему равно значение ?

Вариант 28. Плотность вероятности величины определяется формулой . Выбрать параметры и так, чтобы .

Вариант 29. Известно, что , при этом . Определить значение .

Вариант 30. Случайная величина равномерно распределена на отрезке . Какое распределение имеет величина . Найти её основные числовые характеристики (математическое ожидание, дисперсию и среднеквадратическое отклонение).