
- •1 Цель работы
- •2 Ключевые положения
- •2.1 Кодирование цифровых символов сверточным кодом
- •2.2 Алгоритм сверточного декодирования Витерби в метрике Хэмминга
- •Построение характеристики помехозащищенности при сверточном кодировании в канале с фм - 2
- •3 Домашнее задание
- •4 Контрольные вопросы
- •5 Лабораторное задание
- •6 Содержание протокола
-
1 Цель работы
1.1 Изучение основных принципов помехоустойчивого кодирования и декодирования по алгоритму Витерби сверточных кодов в системах цифровой связи (практическое занятие, 2 часа).
1.2 Исследование корректирующей способности сверточного кода по результатам компьютерного моделирования, определение эффективности кодирования в канале с гауссовым шумом и использованием ФМ-2 при когерентном детектировании (лабораторное занятие, 2 часа).
2 Ключевые положения
2.1 Кодирование цифровых символов сверточным кодом
В представленном материале настоящего подраздела рассматриваются вопросы кодирования двумя сверточными кодами с условными обозначениями (7, 5) и (35, 23), которые обладают свойством исправления соответственно двукратных и трехкратных ошибок. Характерной особенностью этих кодов является то, что они являются несистематическими сверточными кодами (НСК), то есть на выходе кодера в последовательности двоичных символов отсутствуют в неизменном виде информационные биты.
Применительно к кодам (7, 5) и (35, 23), приведенные цифры отображают порождающие многочлены в восьмеричной системе счисления: 7(8) = 111(2) и 5(8) = 101(2), 3_5(8) = 011_101(2) и 2_3(8) = 010_011(2). Для этих кодов порождающие многочлены можно представить и в виде многочленов, а именно:
G1(D) = D2 + D + 1 , G2(D) = D2 + 1;
G3(D) = D4 + D3 + D2 + 1 , G4(D) = D4 + D + 1 .
Функциональные схемы кодеров, с указанными порождающими многочленами G1(D) и G2(D), G3(D) и G4(D), приведены на рис. 2.1.
Как видно из рис. 2.1 а) и б) канальные символы на выходах кодеров (z1, z2), (z3, z4) определяются следующим образом:
z1 = ai ai-1 ai-2 , z2 = ai ai-2 ,
z3 = ai ai-2 ai-3 ai-4 и z4 = ai ai-1 ai-4..
В приведенных выражениях в момент времен i выполняется суммирование по mod 2 информационных символов ai с задержанными ai-1 , ai-2 , ai-3 и ai-4 на интервалы времени 0, 20, 30 и 40 , где 0 численно зависит от скорости модуляции источника дискретного сообщения B = 1/0.
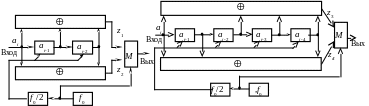

a) б)
Р исунок 2.1 – Функциональные схемы кодеров НСК:
а) – кодер кода (7, 5); б) – кодер кода (35, 23).
При сверточном кодировании выполняется последовательный опрос во времени двух логических состояний на выходах сумматоров канальных символов (z1 z2), а также и (z3 z4). Для этой цели используется мультиплексор M, выполняющий временное уплотнение канальных символов, которые принято называть кодовыми словами.
Важным параметром корректирующего кода является относительная скорость кода R = k0/n0, где k0 - число информационных бит на входе кодера при формировании кодового слова, n0 – число бит в кодовом слове на выходе кодера. Значение этого параметра существенно влияет на корректирующую способность кода и на сложность декодера. Для рассматриваемых кодов в лабораторной работе R=1/2.
Так как кодер НСК (рис. 2.1 а) содержит только две ячейки памяти ai – 1, ai – 2 , ( = 2) обладающих памятью о ранее пришедших двоичных символах, то по существу он представляет собой цифровой автомат с конечным числом состояний 2 = 4. В зависимости от функциональной схемы автомата кодера и его одного из возможных состояний w00 =00 , w10 =10 , w01 =01, w11 =11 кодовое слово в i – тый момент времени (z1 z2)i определяется не только значением входного бита ai, но и внутренним состоянием.
Возможные переходы состояний ячеек памяти кодера ai – 1 и ai – 2 со значениями входных бит ai и выходных кодовых слов (z1 z2)i обычно представляют с помощью графа состояний, что в литературе по цифровым устройствам принято называть диаграммами состояний (ДС).
На рис. 2.2 приведена ДС НСК (7, 5), где в прямоугольных рамках указаны возможные состояния кодера w00 = 00, w10 = 10, w01 = 01 и w11 = 11, которым соответствует содержимое ячеек ai – 1 и ai – 2, образующие последовательный регистр сдвига кодера. На рисунке сплошные линии соответствуют нулевым входным символам, а пунктирные линии – единичным, в круглых скобках указаны выходные кодовые слова кодера. Из приведенной ДС наглядно видно, что существует четыре состояния кодера и только два возможных перехода в разных направлениях, которым соответствуют различные кодовые слова на выходе кодера. Характерной чертой кода (7, 5) и других кодов с R =1/2 является то, что в каждое состояние кодер может прийти только по двум переходам и за один переход перейти из состояния w0 = 00 в состояние w3 = 11 невозможно.
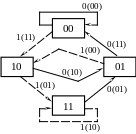
Рисунок 2.2 – Диаграмма состояний кодера НСК (7, 5)
ДС полностью описывает функционирование кодера в фиксированный момент времени, но для отслеживания переходов кодера из одного состояния в другое при изменении моментов текущего дискретного времени ti , i = 0, 1, 2,… возможные переходы удобно представлять в виде повторяющихся ДС в несколько другом геометрическом представлении, что показано на рис. 2.3. На этом рисунке в качестве примера показаны переходы состояний кодера w00 → w10 → w11 → w11 → w01 → w10 для последовательности входных информационных бит ai → 0, 1, 1, 1, 0, 1, 0 и выходных канальных бит (z1 z2)i → 00, 11, 01, 10, 01, 00 , которые отображены жирными сплошными и пунктирными линиями.
ai 0 1 1 1 0 1 0
(z1 z2)i 00 11 01 10 01 00


 w00
w00
w10
w01
w11
t0 t1 t2 t3 t4 t5 t6
Рисунок 2.3 – Решетчатая диаграмма кодера НСК (7, 5)
Диаграмму состояний в таком виде принято называть решетчатой диаграммой (РД). Для кода (7, 5) РД после двух тактовых интервалов, что соответствует выходу кодера из нулевого состояния, обладает периодической структурой. Кодовые ребра (переходы) РД, при входных символах “0”, как и в ДС, представлены сплошными линиями, а кодовые ребра, соответствующие входным символам “1”, пунктирными линиями.
РД кода (35, 23) обладает более сложной внутренней структурой, т. к. в этом случае кодер содержит четыре ячейки памяти ( = 4). Поэтому при кодировании решетчатая структура определяется 2 = 16 состояниями кодера. Для общего представления фрагмент РД для кода (35, 23) приведен в приложении А (см. рис. 1п).
Важным параметром, определяющим корректирующую способность кода, является минимальное кодовое расстояние dmin 2q + 1, где q – кратность исправляемой ошибки. Применительно к сверточным кодам этот параметр определяется на базе представления РД и называется свободным расстоянием или минимальным просветом, обозначаемый символом df [1]. Численно df определяется как минимальный выходной вес пути по РД, начинающийся и заканчивающийся в нулевом состоянии w00 . Как нетрудно убедиться, согласно рис. 2.3 вес пути w00 → w10 → w01 → w00 по решетчатой диаграмме равен Wt = 5, что соответствует битам на выходе кодера 11 10 11 при входных битах 1 0 0. Следовательно, для кода (7, 5) df = 5 , что позволяет исправлять двукратные ошибки на интервалах кодового ограничения n0 ( + 1) = 6 бит .
