
Государственный комитет связи и информатизации Украины
Одесская национальная академия связи им. А. С. Попова
Кафедра теории электрической связи
КОМПЛЕКСНОЕ ЗАДАНИЕ
по курсу Сигналы и процессы в радиотехнике на тему:
ОПИСАНИЕ СИГНАЛОВ ЭЛЕКТРОСВЯЗИ и РАССЧЕТЫ ИХ ХАРАКТЕРИСТИК
Выполнил студент 2-го курса факультета РС, РВ и ТВ
группы Р-41 Носан Ф. Ю.
Руководитель Решетняк О. А.
Комплексное задание проверено и допущено к защите
Руководитель Решетняк О. А.
«___» _______________ 2005 г.
Оценка комплексного задания после защиты ________________
________________
«___» _______________ 2005 г.
Одесса 2005
Содержание
-
Исходные данные для выполнения КЗ 3
-
Задача 1 4
-
Задача 2 8
-
Задача 3 13
-
Задача 4 17
-
Выводы 19
-
Список литературы 20
Исходные данные для выполнения КЗ
|
№ вари-анта |
Форма импульса |
|
|
|
|
Вид аналоговой модуляции |
Вид цифровой модуляции |
|
13 |
Импульс Гаусса |
10 |
30 |
0,02 |
0,5 |
Однополосная |
ЧМ-2 |
Задача 1
Задан импульсный
сигнал
 аналитическим способом. Заданы также:
аналитическим способом. Заданы также:
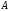 ,
мВ – амплитуда импульса;
,
мВ – амплитуда импульса;
 ,
мс – скорость изменения сигнала.
Необходимо:
,
мс – скорость изменения сигнала.
Необходимо:
а)
рассчитать и построить график сигнала
 ,
определить его длительность;
,
определить его длительность;
б)
найти выражение для спектральной
плотности сигнала
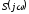 .
Построить график амплитудного спектра
.
Построить график амплитудного спектра
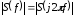 для области значений
для области значений
 ;
;
в)
определить ширину спектра сигнала
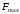 ,
как протяжность интервала
,
как протяжность интервала
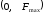 ,
вне которого нормированные значения
амплитудного спектра
,
вне которого нормированные значения
амплитудного спектра
 не превышают заданное значение
не превышают заданное значение
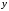 .
.
Решение
а)
Расчет и построение графика заданного
сигнала
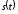
Аналитическая форма импульса:
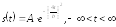
(1.1)
Из аналитической
записи можно утверждать, что функция
четная, максимальное значение импульса
при
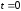 ,
т.е.
,
т.е.
 .
Так как функция
.
Так как функция
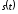 четная, то для построения графика
достаточно рассчитать точки для
четная, то для построения графика
достаточно рассчитать точки для
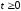 .
При изменении
.
При изменении
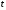 от 0 до
от 0 до
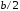 функция
функция
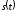 монотонно убывает, поэтому будет
достаточно рассчитать значения функции
в нескольких точках:
монотонно убывает, поэтому будет
достаточно рассчитать значения функции
в нескольких точках:
Таблица 1.1 – Расчетные значения импульса Гаусса
|
|
0 |
2 |
4 |
6 |
8 |
10 |
|
|
10 |
7,52 |
3,2 |
0,77 |
0,1 |
0 |
Рисунок 1.1 –
График заданного импульса Гаусса
б) Получение выражения для спектральной плотности заданного сигнала. Построение графика амплитудного спектра
Так как заданный сигнал – функция четная, то рационально использовать косинус преобразования Фурье:
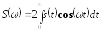
(1.2)
Найдем спектральную плотность сигнала:

(1.3)
Воспользовавшись приложением В из [1], можем записать, что
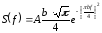
(1.4)
Для построения
графика амплитудного спектра
 ,
необходимо определить шаг для
,
необходимо определить шаг для
 :
:

(1.5)
Результаты расчетов сведем в таблицу 2.
Таблица 1.2 – Расчет графиков амплитудного спектра
|
|
0 |
8 |
16 |
24 |
32 |
40 |
48 |
56 |
64 |
72 |
80 |
|
|
0,133 |
0,128 |
0,115 |
0,097 |
0,075 |
0,055 |
0,037 |
0,023 |
0,014 |
0,007 |
0,004 |
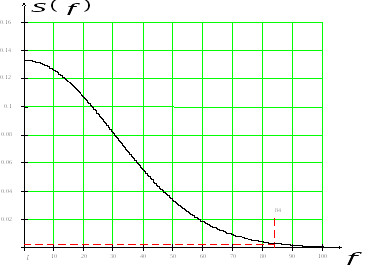
Рисунок 1.2 – Амплитудный спектр импульса Гаусса
в)
Определение максимальной частоты
спектра сигнала

Частота
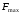 определяется из условий, что значение
амплитудного спектра на частотах
определяется из условий, что значение
амплитудного спектра на частотах
 не превышает заданное значение
не превышает заданное значение
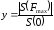 .
Для заданного импульса Гаусса определим
.
Для заданного импульса Гаусса определим
 аналитически.
аналитически.
 – по условию,
следовательно
– по условию,
следовательно

(1.6)
Из выражения (1.4)
выразим
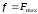 :
:

(1.7)
Подставив значения
 ,
,
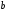 и
и
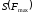 получим:
получим:

(1.8)

 ,
мВ
,
мВ ,
мс
,
мс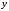
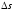 ,
мВ
,
мВ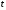 ,
мс
,
мс ,
мВ
,
мВ ,
Гц
,
Гц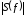 ,
мВ/Гц
,
мВ/Гц