
- •Кафедра высшей математики
- •§ 2. Операции над свободными векторами: сложение и умножение на число.
- •§ 3. Линейная зависимость векторов. Коллинеарность и компланарность векторов.
- •§ 4. Проекции закреплённых и свободных векторов на плоскость и прямую.
- •4.1 Ортогональная проекция на плоскость
- •4.3 Ортогональная проекция на прямую
- •§ 5. Базисы в v3. Координаты векторов относительно базиса.
- •§ 6. Ортогональная система координат в пространстве. Длина вектора.
- •§ 1. Ориентация пространства. Правые и левые тройки некомпланарных векторов.
- •§ 2. Скалярное произведение векторов.
- •§ 3. Векторное произведение векторов.
- •§4. Смешанное произведение векторов.
- •§ 1. Каноническое уравнение плоскости в пространстве
- •§ 2. Канонические и параметрические уравнения прямой в пространстве
- •§3. Расстояние от точки до плоскости в пространстве
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
Государственное образовательное учреждение высшего профессионального образования «Санкт-Петербургский государственный электротехнический университет “ЛЭТИ” имени В.И. Ульянова (Ленина)»
(СПбГЭТУ)
Кафедра высшей математики
Типовой расчет № 1.3
Вариант 15
Выполнил: студент группы 7811 (А.В. Петровский)
Проверил: (К.Ф. Мус)
Санкт-Петербург
2007
Задание
Даны точки:
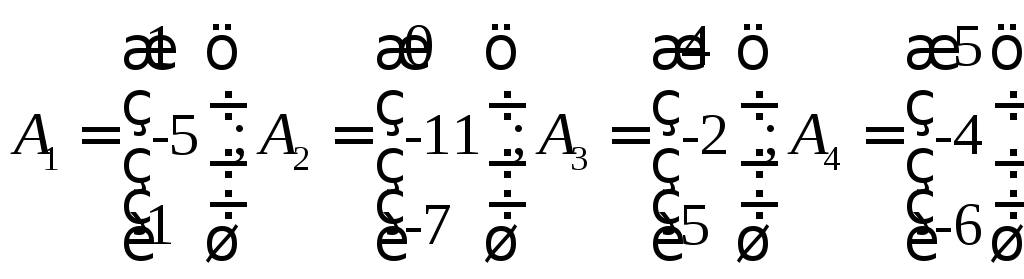
Найти:
уравнение плоскости
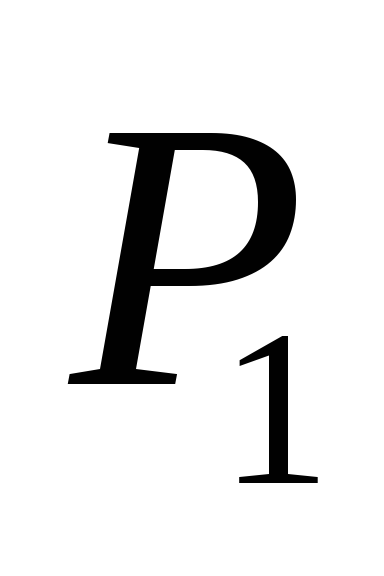 ,
проходящей через точки
,
проходящей через точки ,
, ,
, и плоскости
и плоскости ,
проходящей через точки
,
проходящей через точки ,
, ,
, ;
;уравнение прямой
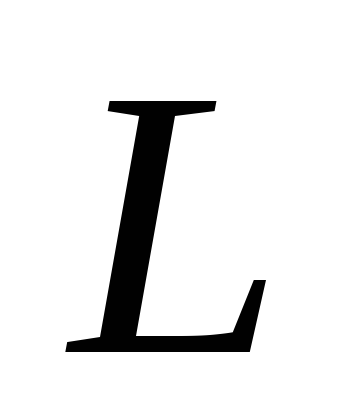 ,
проходящей через точки
,
проходящей через точки и
и ;
;косинус угла
 между
между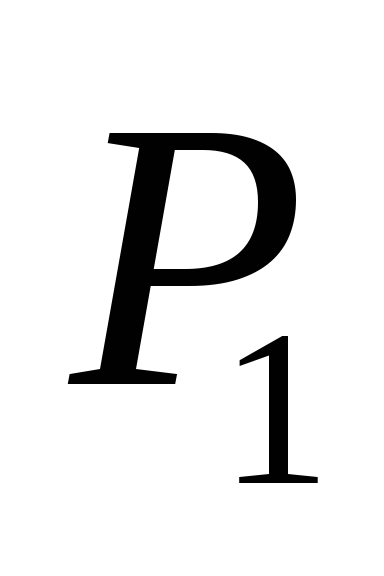 и
и и синус угла
и синус угла между
между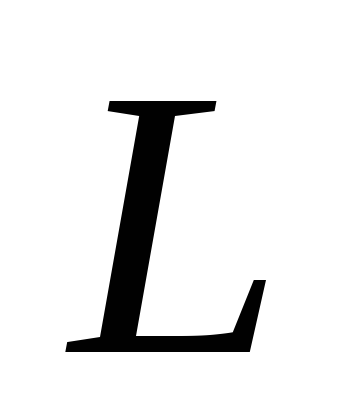 и
и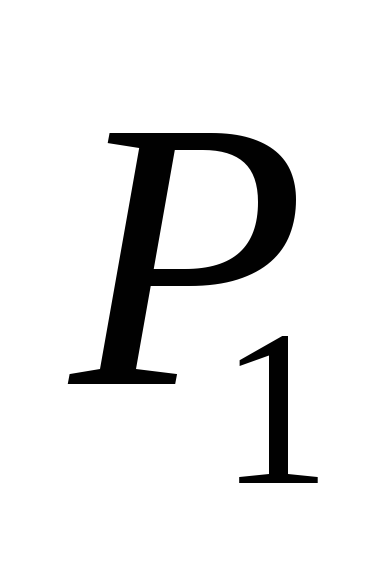 ,
синус угла и углы в радианах;
,
синус угла и углы в радианах;площадь
 треугольника
треугольника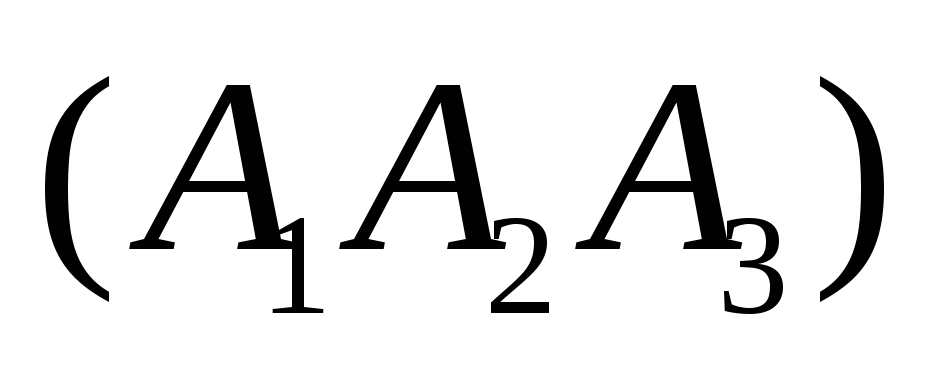 ;
;точку
 ,
симметричную
,
симметричную относительно
относительно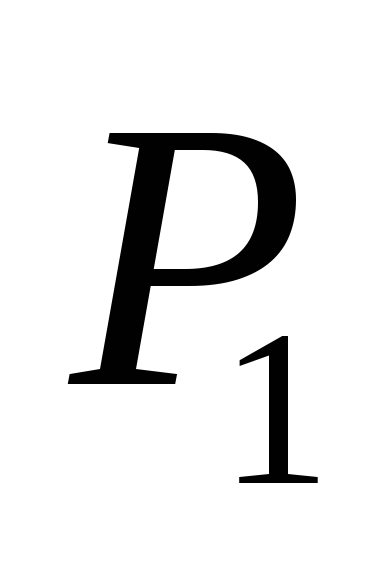 ;
;расстояние
 от
от до
до :
как длина перпендикуляра, из
:
как длина перпендикуляра, из до
до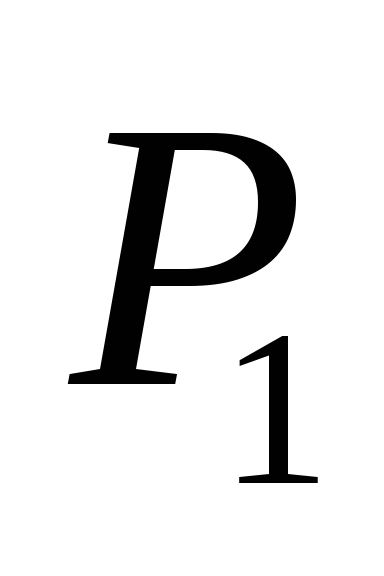 .
.
Определения, обозначения, соотношения, используемые в работе
§ 1. Определения свободного и закрепленного геометрических векторов.
Определение 1: Закрепленный вектор – отрезок с упорядоченными концами: AB,
A – начало вектора, В – конец вектора, АВ ≠ ВА.
Конец и начало вектора могут совпадать: АА – нулевой вектор.
Определение 2: Равенство закрепленных векторов:
Пусть AB и CD – закрепленные ненулевые векторы.
1) Соединим А с С и В с D (начальные и конечные точки векторов).
Если ABDC – параллелограмм, то AB = CD.
2)
AB = CD, если
![]() закрепленный
вектор EF : AB = EF и EF = CD.
закрепленный
вектор EF : AB = EF и EF = CD.
3) Все нулевые векторы равны: АА = ВВ.
Определение 3: Свободный вектор (или просто вектор) – множество равных между собой (в смысле определения 2) закрепленных векторов.
Свободные векторы обозначаются прописными латинскими буквами – a.
Нулевой свободный вектор обозначается θ.
Определение 4: Закрепленный вектор AB является реализацией свободного вектора a, если a = { CD : CD = AB } ( То есть свободный вектор a – это множество закрепленных векторов CD, т.ч. CD = AB. )
Обозначение:
AB
![]() a
(допустимо а
= АВ).
a
(допустимо а
= АВ).
Предложение
1.
![]() с.в.а и
с.в.а и
![]() т.
О пространства
т.
О пространства![]() !
з.в. ОА : ОА
!
з.в. ОА : ОА![]() а.
а.
( Т.е. для любого свободного вектора a и для любой точки О пространства существует единственный закреплённый вектор OA, который является реализацией а. )
Определение 5: Длина свободного вектора a – это длина его реализации:
|a|
= |AB|, если AB
![]() a,
|θ|
= 0.
a,
|θ|
= 0.
Определение
6:
Угол между свободными
векторами а
и b
– это наименьший угол между их реализациями
ОА и ОВ ( ОА![]() а,
ОВ
а,
ОВ![]() b
).
b
).
Определение 7: Свободные векторы a и b равны (a = b), если они совпадают как множества.
Из
определения свободного вектора очевидно,
что для того, чтобы задать свободный
вектор a, достаточно задать какую-либо
его реализацию, т.е. закрепленный вектор
AB
![]() a.
a.
Определение 8: V3 – множество всех свободных векторов в пространстве R3.
§ 2. Операции над свободными векторами: сложение и умножение на число.
Определение 9: Сумма свободных векторов.
Пусть
a, b
![]() V3.
Возьмем произвольно точку О.
V3.
Возьмем произвольно точку О.
Тогда
![]() !
ОА
!
ОА![]() a
и
a
и
![]() !
AB
!
AB![]() b
т.ч. OB
b
т.ч. OB
![]() a+b,
т.е. a+b
= { CD : CD = OB}
a+b,
т.е. a+b
= { CD : CD = OB}
Корректность
сложения: OB
![]() a+b,
O'B'
a+b,
O'B'
![]() a+b
a+b
![]() OB
= O'B'.
OB
= O'B'.
Определение 10: Пусть a - свободный вектор, AB – его реализация, тогда BA является реализацией свободного вектора (-a).
(-a)
– обратный вектор для
a, т.е. (-a)
= { BA : AB
![]() a
}
a
}
Определение 11: Умножение вектора на число:
1)
λ•θ
= θ
для
![]() λ
λ![]() R.
R.
2)
a ≠
θ,
AB
![]() a,
отрезок AB лежит на прямой l.
a,
отрезок AB лежит на прямой l.
2.1)
λ = 0
![]() λ∙a
=
θ.
λ∙a
=
θ.
2.2)
λ > 0
![]() AC
AC![]()
![]() λ∙a,
где AC т.ч. |AC| = λ•|AB|, C
λ∙a,
где AC т.ч. |AC| = λ•|AB|, C
![]() l
и т. B и C находятся по одну сторону от т.
А.
l
и т. B и C находятся по одну сторону от т.
А.
2.3)
λ < 0
![]() AD
AD![]() λ∙a,
где AD т.ч. |AD| = |λ|∙|AB|, D
λ∙a,
где AD т.ч. |AD| = |λ|∙|AB|, D
![]() l
и т. B и D находятся по разные стороны от
т. А.
l
и т. B и D находятся по разные стороны от
т. А.
Свойства
операций над векторами:
![]() a,
b, c
a,
b, c
![]() V3
,
V3
,
![]() λ,
μ
λ,
μ![]() R
R
1) Коммутативность сложения
a + b = b + a.
2) Ассоциативность сложения
a + b + c = (a + b)+ c = a +( b + c).
3) a + θ = a.
4) a +(-a) = θ.
5) Ассоциативность умножения на число
λ(μ∙ a) = (λμ)∙ a
6) 1∙ a = a.
7) Дистрибутивность умножения на число относительно сложения векторов
λ∙( a + b) = λ∙ a +λ∙ b.
8) Дистрибутивность умножения на число относительно сложения чисел
(λ+μ)∙ a = λ∙ a +μ∙ a.
