14

ОФ-ВМ-1 «Алгебра» 1

Глава I. Числовые множества. 1

Введение. 1

§1. Множества : символика, операции; числовые множества NÌZÌQÌR 2

§2 Множество комплексных чисел(к.ч.) : определения, аксиомы, комплексная плоскость; RÌC. 4

§3. Алгебраическая форма к.ч.; арифметические операции с к.ч. 6

§4. Тригонометрическая и показательная формы к. ч. ; аргумент к. числа. 8

§5.Решение двучленных zn=a и квадратных z2+bz+c=0 уравнений в С; основная теорема алгебры. 11

ОФ-ВМ-1 «Алгебра»

Глава I. Числовые множества.

Введение.

Алгоритм курса ВМ. Символические обозначения.

Пусть А,В – утверждения, высказывания

1) импликация ==>

AB :«из А следует В», «если А, то В»;

2) равносильность, эквивалентность 

AB «А и В равносильны»,

«одновременно: A=>B и B=>A»;

3)дизъюнкция V A V B : «хотя бы одно их двух», «А или В»

4) конъюнкция  А  В : «А и В одновременно»

5) квантор существования  - «существует», «найдется»

а:А(а) : «существует (найдется) такое а, для которого имеет место А(а)»;

6) ! – «существует единственное», «существует и единственно»

!а:А(а) : «существует (найдется) такое единственное а, для которого имеет место А(а)»;

7) квантор всеобщности  -«для любого», а:А(а) :«для любого а верно А(а)»;

=



8) - «обозначим», «по определению»: f(х)=xsin(2x).

Например, символьная запись а0 b: ab=1 определяет «обратное число» : «для любого не равного нулю числа а существует такое «обратное число b», что их произведение равно единице».

----------------------------------------------------------

Д/З: запишите в символьном виде теорему: «Если дискриминант D квадратного уравнения ax²+bx+c=0 равен нулю, уравнение имеет единственное решение».

§1. Множества : символика, операции; числовые множества nìzìqìr

Множество, система, совокупность, набор – исходные непределимые понятия. Говорят: «множество целых чисел», «система уравнений», «набор инструментов», «совокупность решений» т т.п.

Множество считается заданным, если указаны все его элементы, например A={a;F(a)} - задано «условию принадлежности» F(a). Для числовых множеств в качестве F(a) используют список, уравнение, неравенство.

Введем для множеств символьные обозначения.

• Символы принадлежности “”, “” – «(не)принадлежит», «(не)является элементом» множества.

Например, множество A={1,2,{3,4}} имеет три элемента: 1А; 2A;{3,4)A, но 3А. X={x; x³-6x²+11x-6=0}={1,2,3} - множество решений уравнения F(x) : x³-6x²+11x-6=0.

• «» - “пустое множество”(множество, не имеющее ни одного элемента !!). например, 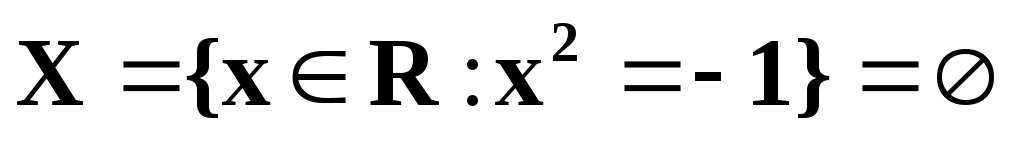, НО не допустима записьx !!!  «Квадратное уравнение х²+1=0 во множестве R решений НЕ ИМЕЕТ»

• Символ включения «»: 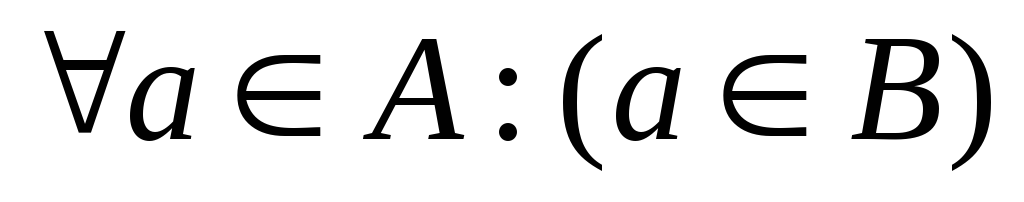 - «множество А содержится в В, является подмножеством (частью) множества В»;

например, A={1,2,{3,4}} 2A, НО {2}A.

Очевидно, что

ПустьA={a}; B={b} и C={c}. Элементы множества изобразим внутренними точками “круга Эйлера”

a dA

A

Введем операции над множествами :

1.Равенство множеств «=» : А = В Û "аÎА "bÎB (аÎB  bÎA)

2. Объединение множеств «È»: AÈB = C Û "cÎC ( cÎA V cÎB)

«Объединением множеств называется множество, состоящее только из тех элементов, которые принадлежат хотя бы одному из этих множеств (А ИЛИ В).»

3. Пересечение множеств «Ç»: AÇB = C Û "cÎC (cÎB  cÎA)

4. Разность множеств « /» : C = A / B Û "cÎC(cÎB  cÏB)

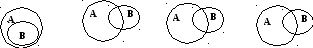
BA C=AB C=AB C=A/B

«ЗНАНИЕ»: в средней школе введены числовые множества:

N={1,2,…} - множество натуральных чисел,

Z={0,±1,±2,…} - множество целых чисел,

Q={} - множество рациональных чисел(рац. дробей),

R - множество вещественных (действительных) чисел,

Во множестве вещественных (действительных) чисел R:

[1]введены специальные обозначения-интервалы : ]a,b[ , [a,b], [a,b[, ]a,b] - открытый, закрытый, открытый справа и /или слева.

[2]определены операции:

равенства “=”, сложения “+”, вычитания “-“,сравнения (неравенства строгие >, < - «больше, меньше» и нестрогие ;  - « не больше, не меньше”; 2  3 – «2 не больше 3» !!), умножения “x”, деления “:”(исключая деление на число «0»), возведения в натуральную степень aRnN:aⁿ=aa…a;

[3] определены: “модуль числа |a|”: ;

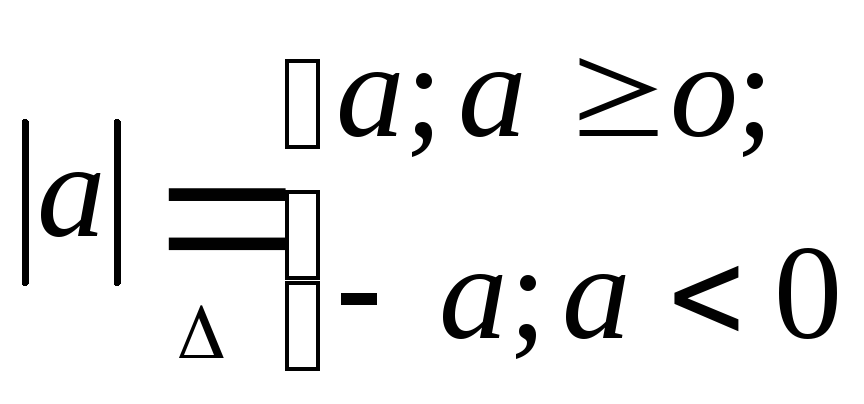и “арифметическое значение корня натуральной степени”

[4] не определено деление на ноль;

[5] каждой точкечисловой прямой поставлено в соответствие единственное вещественное число - ее координата;

В дальнейшем будем отождествлять точку числовой прямой М(х) и вещественное число xи будем, например, говорить:sin(2) «значение функции “sin” в точке х=2».

--------------------------------------------------------------------