
- •Кафедра высшей математики
- •§ 2. Операции над свободными векторами: сложение и умножение на число.
- •§ 3. Линейная зависимость векторов. Коллинеарность и компланарность векторов.
- •§ 4. Проекции закреплённых и свободных векторов на плоскость и прямую.
- •4.1 Ортогональная проекция на плоскость
- •4.3 Ортогональная проекция на прямую
- •§ 5. Базисы в v3. Координаты векторов относительно базиса.
- •§ 6. Ортогональная система координат в пространстве. Длина вектора.
- •§ 1. Ориентация пространства. Правые и левые тройки некомпланарных векторов.
- •§ 2. Скалярное произведение векторов.
- •§ 3. Векторное произведение векторов.
- •§4. Смешанное произведение векторов.
- •§ 1. Каноническое уравнение плоскости в пространстве
- •§ 2. Канонические и параметрические уравнения прямой в пространстве
- •§3. Расстояние от точки до плоскости в пространстве
§4. Смешанное произведение векторов.
Определение 4: Смешанным произведением упорядоченной тройки векторов a, b и c называется число <a, b, c>, т.ч. <a,b,c>=([a,b],c).
Утверждение 3: <a,b,c>=Va,b,c, если a,b,c – правая тройка, или <a,b,c>= -Va,b,c, если a,b,c – левая тройка. Здесь Va,b,c – объём параллелепипеда, построенного на векторах a, b и c. (Если a, b и c компланарны, то Va,b,c=0.)
Утверждение 4: В декартовой системе координат, если a={x1, y1, z1}, b={x2, y2, z2},
с={x3,
y3,
z3},
=> <a,b,c>= .
.
Каноническое уравнение плоскости ~ Канонические и параметрические уравнения прямой ~ Расстояние от точки до плоскости ~ Координаты точки, делящей отрезок в заданном соотношении
§ 1. Каноническое уравнение плоскости в пространстве
Пусть в декартовой системе координат дан вектор n={A,B,C} и точка М0=(x0,y0,z0).
Построим плоскость Π, проходящую через т. М0, перпендикулярную вектору n (этот вектор называют нормальным вектором или нормалью плоскости).
Утверждение
1: М
![]() Π
М0М
Π
М0М
![]() n.
n.
М0М={x-x0,
y-y0,
z-z0}
![]() n
A(x-x0)+B(y-y0)+C(z-z0)=0.
(*)
n
A(x-x0)+B(y-y0)+C(z-z0)=0.
(*)
(См. свойства скалярного произведения)
Каноническое уравнение плоскости в пространстве:
Аx+By+Cz+D=0, где D = -Ax0-By0-Cz0.
Замечание 1: формула (*) используется при непосредственном решении задач, после упрощения получается искомое каноническое уравнение плоскости.
§ 2. Канонические и параметрические уравнения прямой в пространстве
Пусть в декартовой системе координат дан вектор a={p,q,r} и точка М0=(x0,y0,z0).
Построим прямую l, проходящую через т. М0, параллельную вектору a (этот вектор называют направляющим вектором прямой).
Утверждение
2: М![]() l
М0М
|| a.
l
М0М
|| a.
М0М={x-x0,
y-y0,
z-z0}
|| a
![]() t
t![]() R,
т.ч. М0М=t·a
=>
R,
т.ч. М0М=t·a
=>

Параметрические уравнения прямой в пространстве:
 (**)
(**)
Вы никогда не сталкивались с параметрическим заданием кривых? Поясним на примере: представьте себе, что по заранее намеченному маршруту с известной скоростью движется турист (автомобиль, самолёт, подводная лодка, как Вам больше понравится). Тогда, зная точку начала его путешествия, мы в любой момент времени знаем, где он находится. Таким образом, его положение на маршруте определяется всего одним параметром – временем.
В нашем случае турист движется по бесконечной прямой в пространстве, в момент времени t0=0 он находится в точке М0, в любой другой момент времени t его координаты в пространстве вычисляются по формулам (**).
Теперь несколько преобразуем формулы (**).
Выразим
из каждой строчки параметр t:

Канонические уравнения прямой в пространстве:
![]()
Замечание 2: Эта компактная запись на самом деле содержит три уравнения.
Замечание
3: Это формальная запись и выражение
вида
![]() в
данном случае допустимо.
в
данном случае допустимо.
Замечание 4: Надо понимать, что для уравнения плоскости (прямой) играет роль именно направление перпендикулярного (направляющего) вектора, а не он сам. Т.о. вполне допустимо из каких-либо соображений заменять данный (или полученный в ходе решения) вектор на пропорциональный ему. Целесообразно также упрощать полученное уравнение, деля все его коэффициенты на общий множитель.
§3. Расстояние от точки до плоскости в пространстве
Пусть в декартовых координатах плоскость Π задана уравнением: Ax+By+Cz+D=0, а точка М1=(x1,y1,z1).
Утверждение 3: расстояние от точки М1 до плоскости Π вычисляется по формуле:
![]()
Выполнение работы




1)
а) 



Уравнение плоскости:
![]()
![]()
![]()
![]() (*)
(*)
б) 



Уравнение плоскости:
![]()
2)
![]()
![]()
 Изометрическое
уравнение прямойL.
Изометрическое
уравнение прямойL.
3)
![]()
![]()

![]()
![]() рад
рад
![]()
![]()

![]()
![]() рад
рад
4)
![]()
![]()
![]()




![]()
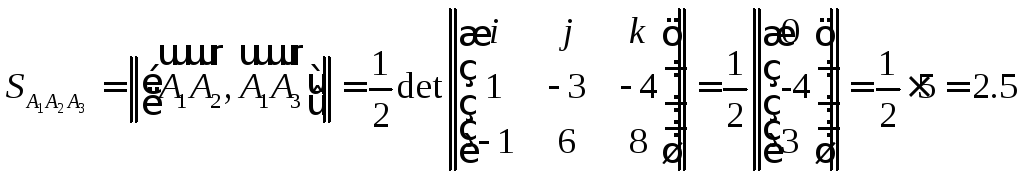
6)

![]()
![]()


уравнение перпендикулярности из
![]() к
плоскости
к
плоскости![]()



С(-11,8,6)

![]()
7)

Результаты:
Вариант 19
1)
а)
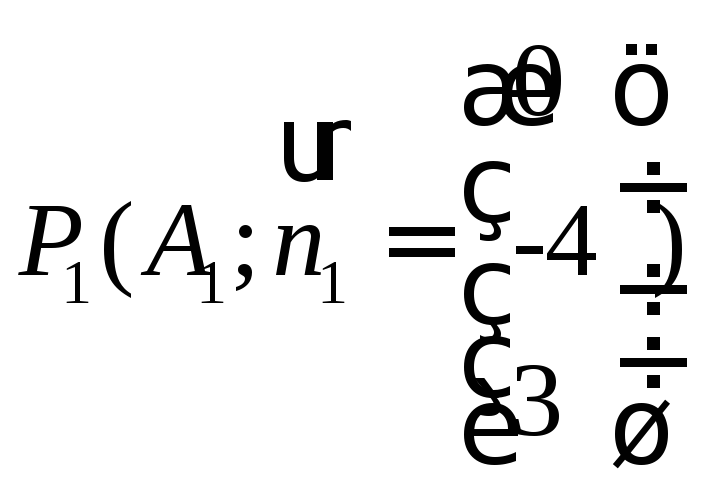
![]()
б)

![]()
2)
![]()

3)
![]()
![]() рад
рад
![]()
![]() рад
рад
4)
![]()
6)
![]()
 С:
С:
7)
![]()
