§ 3. Линейная зависимость векторов. Коллинеарность и компланарность векторов.

 

Определение 12: Векторы а₁, а₂, … , а_n коллинеарны, если существует прямая l, содержащая реализацию каждого из них.

Обозначение: а || b

Предложение 2: a || b  λ R, т.ч. a= λ∙b

 

Определение 13: Коллинеарные векторы а и b одинаково направлены, если ОАа, ОВb и т. А и В лежат по одну сторону от т. О.

Обозначение: а b

 

Определение 14: Коллинеарные векторы а и b разнонаправлены, если ОАа, ОВb и т. А и В лежат по разные стороны от т. О.

Обозначение: а b

 

Определение 15: Векторы а₁, а₂, … , а_n компланарны, если существует плоскость в пространстве, содержащая реализацию каждого из них.

Пример : рассмотрим с.в. е_а=а( а≠ θ ).

е_а коллинеарен а, одинаково направлен с а, |e_a|=1.

Замечание: Любые два свободных вектора компланарны. Нулевой вектор имеет реализацию на любой плоскости в пространстве. Следовательно, три вектора: а, b, θ всегда компланарны.

Определение 16: Система векторов а₁, а₂, … , а_n линейно зависима, если λ₁, λ₂, …, λ₃R, не все равные нулю, такие что λ₁· а₁+ λ₂· а₂+ λ_n· а_n=0

 

Определение 17: Если λ₁· а₁+ λ₂· а₂+ λ_n· а_n=0 только при λ₁ = λ ₂ = … = λ₃ = 0, то система векторов а₁, а₂, … , а_n линейно независима.

 

Предложение 3:Любая система из трёх и более ненулевых компланарных векторов линейно зависима.

Предложение 4:Любые три некомпланарных вектора линейно независимы.

§ 4. Проекции закреплённых и свободных векторов на плоскость и прямую.

 

Проецирование точек на плоскости и прямые хорошо изучается в школьном курсе геометрии, так что остаётся уговориться об обозначениях:

пр_Π М; – ортогональная проекция т. М на плоскость Π,

пр_m М; ( || l ) – проекция т. М на прямую m параллельно прямой l

4.1 Ортогональная проекция на плоскость

 

Определение 18: Пусть А₁= пр_Π А, В₁= пр_Π B A₁B₁= пр_Π AB.

( Т.е. з.в. A₁B₁ – это ортогональная проекция з.в. AB на плоскость Π )

 

Определение 19: Пусть АВ а ипр_Π AB а₁ а₁= пр_Π а.

( Т.е. с.в. а₁ – это ортогональная проекция с.в. а на плоскость Π )

 

4.2 Общий случай проецирования на плоскость. ( Проецирование параллельно прямой l которая не || и не лежит на плоскости Π )

 

Начало и конец вектора проецируются на Π параллельно l , определения вводятся аналогично п. 4.1 .

 

4.3 Ортогональная проекция на прямую

 

Определение 20: Пусть А₁= пр_m А, В₁= пр_m B A₁B₁= пр_m AB.]

Определение 21: Пусть АВ аи пр_m AB а₁ а₁= пр_m а.

 

4.4 Общий случай проецирования на прямую. ( Проецирование параллельно прямой l которая не || и не совпадает с прямой m )

 

Начало и конец вектора проецируются на m параллельно l , определения вводятся аналогично п. 4.3 .

§ 5. Базисы в v3. Координаты векторов относительно базиса.

 

Определение 22: Базисом в пространстве свободных векторов V₃ называется любая упорядоченная тройка некомпланарных векторов.

 

Пусть В : а₁, а₂, а₃ – фиксированный базис в V₃.

 

Определение 23: Координатами вектора b относительно базиса В называется упорядоченная тройка чисел {x, y, z}, т.ч. b=x·a₁+ y·а₂+z· а₃.

Обозначение: b={x, y, z}_B

Замечание: Под координатами закреплённого вектора понимают координаты соответствующего ему свободного вектора.

 

Теорема1: Соответствие между V₃ и R³ при фиксированном базисе взаимно однозначно, т.е. b V₃ ! {x, y, z}R³ и {x, y, z}R³ !b V₃, т.ч. b={x, y, z}_B

Соответствие между вектором и его координатами в данном базисе обладает следующими свойствами:

1. Пусть b₁={x₁, y₁, z₁}_B, b₂={x₂, y₂, z₂}_B b₁+ b₂={x₁+ x₂, y₁+ y₂, z₁+ z₂}_B

2. Пусть b={x, y, z}_B, λ 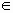Rλ·b={ λ·x, λ· y, λ·z}_B

3. Пусть b₁|| b₂, b₁= {x₁, y₁, z₁}_B, b₂={x₂, y₂, z₂}_B (Здесь:любое число).

Определение 23: Ортонормированный ( декартов ) базис – это i, j, k, т.ч.

1) | i |=| j |=| k |=1,

2) i j k i.