2). Матричные коммутаторы

Матричные коммутаторы (crossbar network )являются одним из наиболее гибких типов соединительных сетей. Обобщенная структура матричного коммутатора, обеспе­чивающего соединение М на L портов, представлена на рис.2.

Рис. 2. Два представления M х L - матричного переключателя

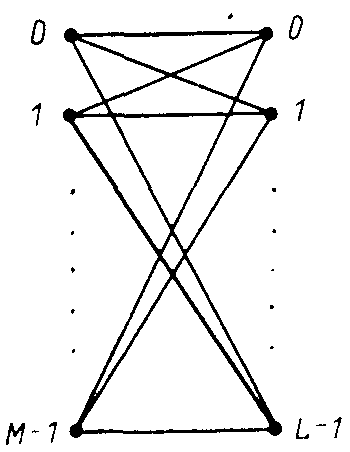
Сеть коммутации представляет собой множество связей между двумя наборами узлов, которые называются входами и выходами. Всего между M входами и L выходами существует M^L раз личных связей, включая парные связи («один — одному»), связи «один—многим», смешанные связи.

Рис.3. Варианты соединений в обобщенной соединительной сети для M=3, L=2:

a — связи «ОДИН — МНОГИМ» ;

б, в — парные связи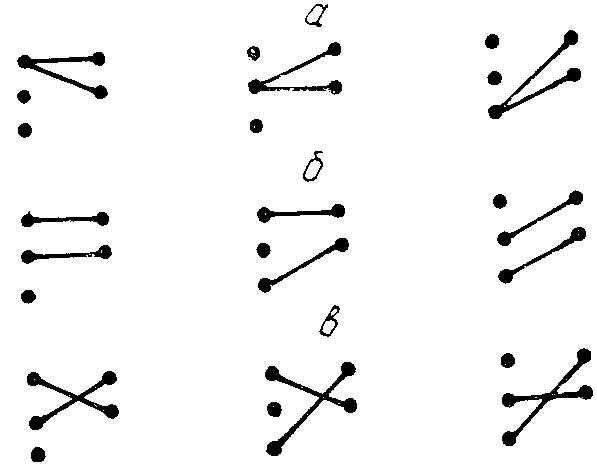

Сеть, осуществляющая M^L соединений, называется обобщенной соединительной сетью (рис. 3). Если сеть осуществляет только парные связи, она называется соединительной, в ней возможно M! соединений (рис. 3, б, в). В соединительных сетях любой допустимый набор связей (перестановка) выполняется за один такт и без конфликтов.

Организация матричного коммутатора такова, что при отсутст­вии конфликтов все необходимые связи обеспечиваются одно­временно. Конфликты возникают, когда два или более абонен­та требуют коммутации одного и того же узла. Понятно, что в каждом узле необходимо разрешать возникающие конфликты. Поэтому узел коммутации может представлять собой достаточ­но сложную схему.

Одной из разновидностей матричного коммутатора является сеть, называемая «полное соединение» (complete connection). В ней для установления связи каждого из М портов с L портами используются собственные L линий связи (рис. 2,б). Легко заметить, что число узлов коммутации в этом случае остается прежним.

Так как число узлов коммутации растет пропорционально произведению ML, то стоимость матричных коммутационных сетей при большом количестве портов весьма высока. Однако при малом числе соединяемых блоков они эффективно исполь­зуются, в частности, и для упорядочения данных в параллель­ной памяти.

3). Многоярусные коммутационные сети

Когда количество портов, соединяемых коммутационной сетью, исчисляется сотнями или тысячами, использование мат­ричных коммутаторов не представляется возможным из-за их высокой сложности и стоимости. Не эффективными оказывают­ся и конвейерные соединители, обладающие в этом случае весьма низким быстродействием. Решением проблемы является использование многоярусных коммутационных сетей. Много­ярусные сети строятся из нескольких ярусов коммутационных элементов (КЭ). КЭ может сам представлять некоторую сое­динительную сеть, например матричный переключатель. Чаще всего на практике используются простые КЭ с двумя входами и двумя выходами.

Выделяют три основных вида многоярусных сетей: неблокируемые сети, перестраиваемые и блокируемые сети.

Неблокируемые сети.

Если коммутационная сеть находится в состоянии, при котором невозможно найти путь соединения определенного незанятого входного порта с незанятым выходным, то говорят, что эта сеть заблокирована. Неблокируемыми, следовательно, называются такие сети, в которых всегда можно найти путь соединения для свободной пары портов.

Неблокируемые структуры получаются путем введения до­полнительных ярусов коммутации. Несмотря на это многоярусные неблокируемые сети часто более экономичны, чем матричные коммутаторы. Так, например, число КЭ в матричном коммутаторе для М = L = 25 (двадцать пять входов соединяются с двадцатью пятью выходами) равно 625, в трехярусной схеме Клоза - 675, но при М = L = 100 для матричного коммутатора число КЭ уже 10000, a в схеме Клоза - 5700.

Перестраиваемые сети.

Близки к неблокируемым. Перестраиваемыми они называются потому, что могут выполнить, все возможные соединения между входными и выходными

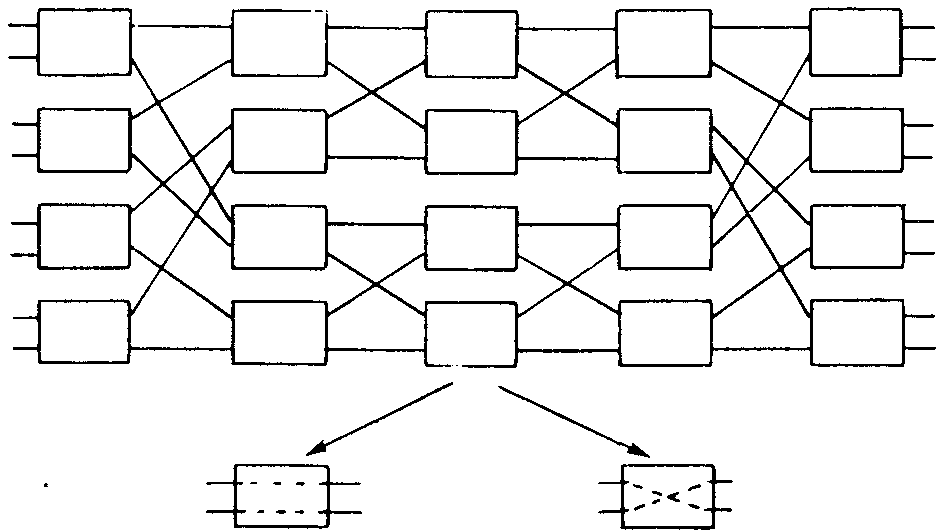
Рис. 4. Сеть Бенеша

портами, перестраивая существующие связи так, как этого требует установление незаблокированного пути для новой за­данной пары портов. Структурная схема такой сети, называе­мой сетью Бенеша, представлена на рис. 4.

Неблокируемые и перестраиваемые сети, обеспечивая высо­кую гибкость и полноту коммутации, остаются все же доста­точно сложными по структуре и соответственно требуют слож­ного управления. Они безусловно могут использоваться для упорядочения данных в параллельной памяти, однако их применение не все­гда целесообразно. В большинстве случаев задача упорядоче­ния решается при некотором ограниченном наборе коммутации и не требует выполнения условий неблокируемости. В связи с этим большой интерес представляют блокируемые многоярус­ные сети.

Блокируемые сети.

Одним из обоб­щений блокируемых сетей являются Бэнян-сети, которые введены Р. Гоуком и К. Липовским и использовались для построения мультипро­цессорной архитектуры. Свое название они получили oт фигового дерева (banyan-tree). Авторы, очевидно, имели в ви­ду определенное топологическое сходство индийской смоковни­цы и соответствующего графа.

Граф, описывающий структуру Бэнян-сети, содержит три типа вершин: начальные, не имеющие входящих ребер, конеч­ные, не имеющие исходящих ребер, и промежуточные. Послед­ние имеют и входящие, и выходящие ребра. На рис. 5. приве­дены примеры Бэнян-сетей. Во всех диаграммах начальные вершины размещены внизу, а конечные - наверху.

Отметим некоторые топологические особенности Бэнян-сетей. Сеть, в которой каждый путь, от начальной вершины к ко­нечной имеет длину l и для каждой пары <начальная верши­на—конечная вершина> этот путь является единственным,

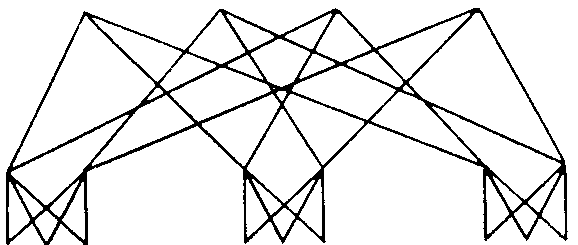
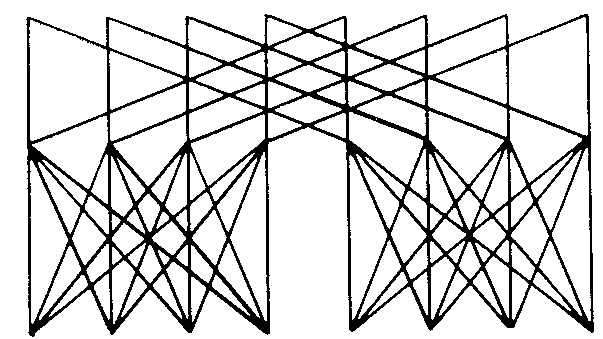
Рис. 5. Бэнян-сети.

называется l-уровневой Бэнян-сетью. В такой сети имеется l уровней (ярусов) ребер и l + 1 уровней вершин. В l -уровневых Бэнян-сетях ребра связывают только вершины соседних уров­ней. Примем, что начальные вершины размещаются на уровне 0, а конечные - на уровне l. В дальнейшем рассматриваются только однородные Бэнян-сети, в которых для всех вершин од­ного уровня число входящих и число выходящих ребер есть ве­личины постоянные. Структуру однородной Бэнян-сети можно охарактеризовать, если указать число вершин на каждом уров­не L₀, L₁, …,L_l и для вершин каждого уровня число входящих (c) и выходящих (0) ребер. Так как в l-уровневой сети l ярусов ребер, то соответствующее описание всей сети задается l-ком­понентными векторами с= (с₁, с₂, ..., с_l), о= (o₁, o₂, ..., o_l) и вектором L= (L₀, L₁, ..., L_l).

Бэнян-сеть называется регулярной, если с₁= с₂= ...= с_l и o₁= o₂= ...= o_l (рис. 5,а), в противном случае сеть нерегулярна (pиc. 5,б). Важное место в классе Бэнян-сетей занимают прямоугольные сети. Сеть является прямоугольной, если L₀= L₁= ...= L_l и с = о. Нерегулярные прямоугольные Бэнян-сети называются слабо прямоугольными (pиc. 5,в), регулярные - строго прямоугольными (рис. 5,г).

Еще одним обобщенным видом блокируемых многоярусных систем являются Дельта-сети.

Строго прямоугольные Бэнян-сети с числом узлов на каж­дом уровне L = 2¹, построенные на 2 X 2-матричных переклю­чателях, составляют особый подкласс сетей. Эти сети называются двоичными перестановочными (или просто перестано­вочными) сетями. К ним можно отнести такие широко известные сети как Омега-сеть, сеть типа двоичный n-Куб, моди­фицируемый манипулятор данных, базисная сеть.

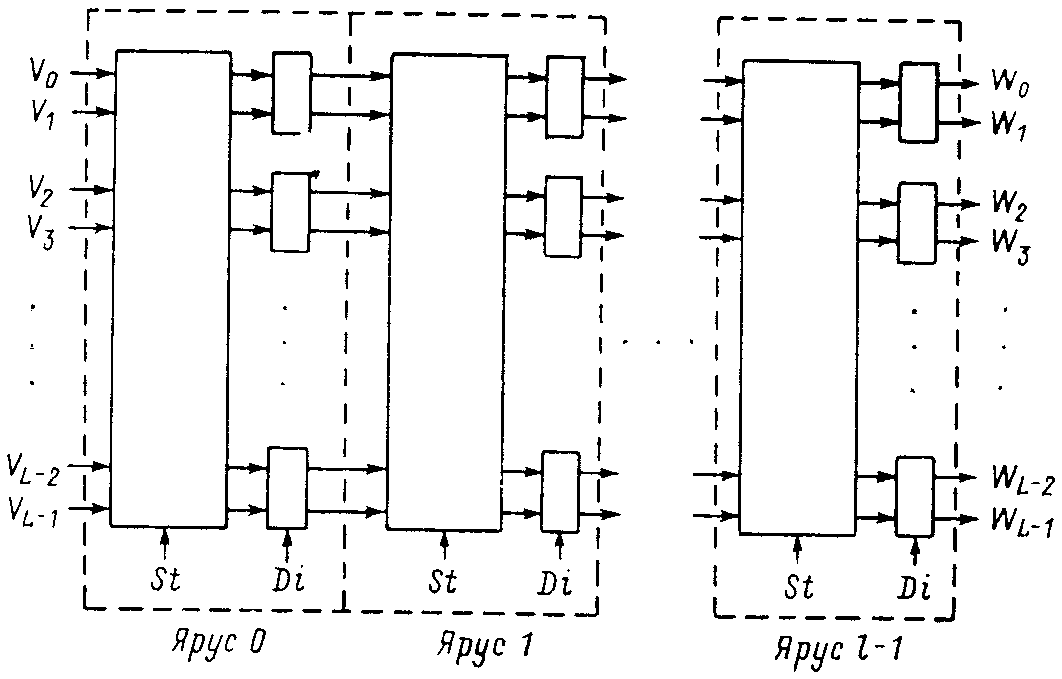
Рис. 6. Обобщенная структура двоичной перестановочной сети.

Обобщенная двоичная перестановочная сеть может быть представлена log₂L = l ярусами коммутационных элементов, соединенных между собой по определенному закону. Сеть, рас­сматриваемая как однонаправленная, осуществляет передачу данных от входа к выходу. Каждый ярус сети может быть представлен как два устройства, выполняющих последователь­но две перестановки (рис. 6). Одна из них - статическая (St) осуществляется за счет того, что линии связи между ярусами могут изменять позицию при входе в следующий ярус. Стати­ческая перестановка определяется выбранным законом межярусных соединений, она зафиксирована для конкретного вида сети. Вторая, динамическая перестановка (Di), осуществляется коммутационными элементами, и ее содержание определяется выбранным способом управления сетью, а также видом КЭ.

В двоичных перестановочных сетях в качестве КЭ используются 2 Х 2-переключатели двух типов (рис. 7, а, б). Модель КЭ первого типа составлена из двух мультиплексоров 2 X 1, управляемых независимо. Такой КЭ может находиться в четырех различных состояниях, определяемых управляющим сигналами c₁, c₀. Коммутационные элементы второго типа имеют только два состояния включения и управляются единственным управляющим сигналом с. Мы рассматриваем двоичные перестановочные сети как устройства упорядочения данных в параллельной памяти.

а)

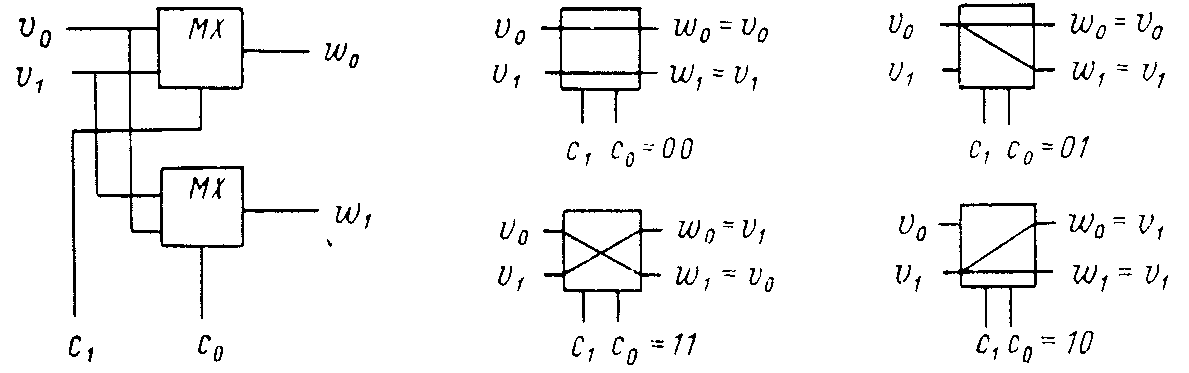
б)

Рис. 7. Структуры коммутационных элементов

Динамическая перестановка полностью оп­ределяется состоянием управляющих сигналов, подаваемых на коммутационные элементы соответствующих ярусов, и, следо­вательно, при одинаковом управлении динамические переста­новки в разных l-ярусных двоичных перестановочных сетях совпадают. Общие перестановки, выполняемые этими сетями, различаются только вследствие разных межярусных соедине­ний, т. е. разных статических перестановок.

Рассмотрим и сравним между собой несколько конструкций сетей. На рис. 8 - 10 показаны соответственно Омега-сеть, базисная сеть и n-Куб-сеть.

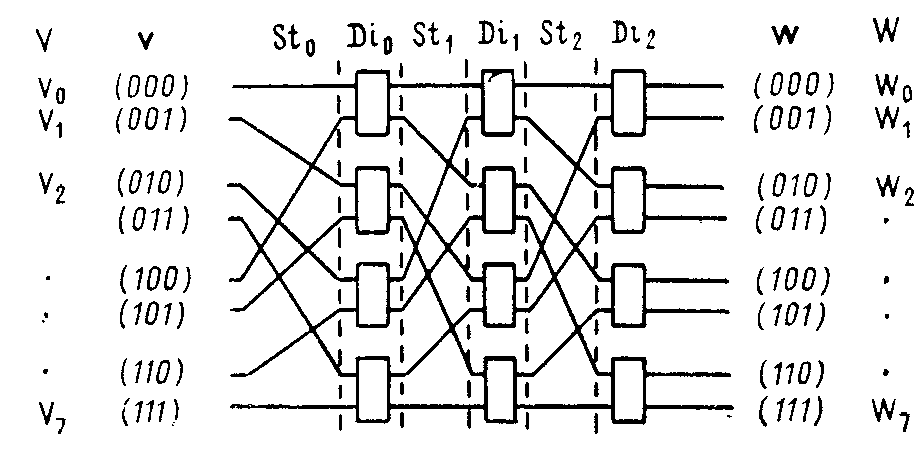
Рис. 8. Омега-сеть, L = 8.

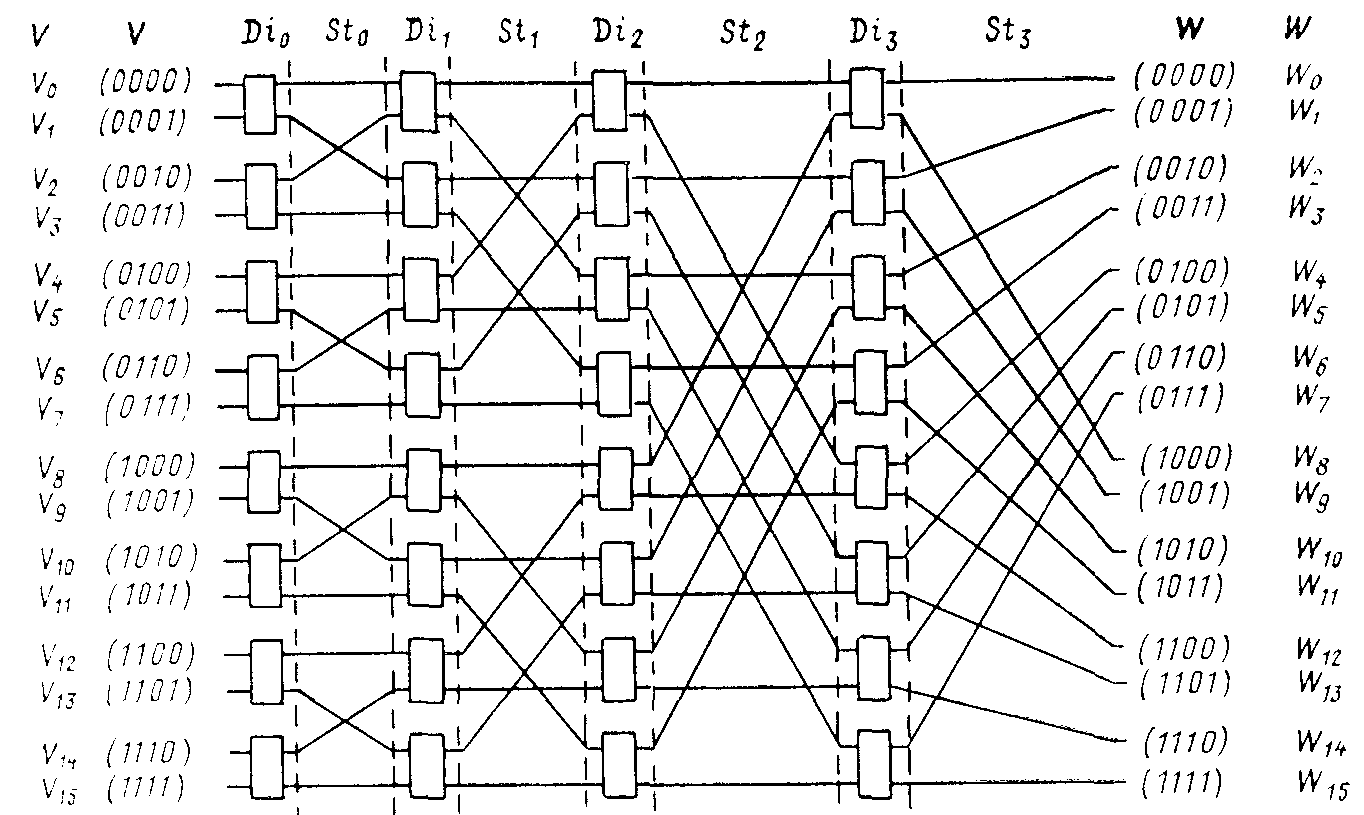
Рис. 9. Базисная сети, L = 16.

Рис. 10. n – Куб-сеть, L = 16.

Рассмотрим двумерный коммутатор. Каждый процессорный элемент (ПЭ) соединен двусторонними связями с четырьмя соседними (справа, слева, снизу, сверху) (рис. 11, а). Внешние связи могут в зависимости от решаемой задачи программно замыкаться по-разному: вытягиваться в цепочку (рис. 11, б), замыкаться в виде вертикально (рис. 11, в) и горизонтально (рис. 2.11, г) расположенных цилиндров, в виде тороида (рис. 11, д). Коммутационный элемент (КЭ) здесь обычно соединен с оборудованием ПЭ, и объем оборудования всего коммутатора растет пропорционально числу процессоров M.

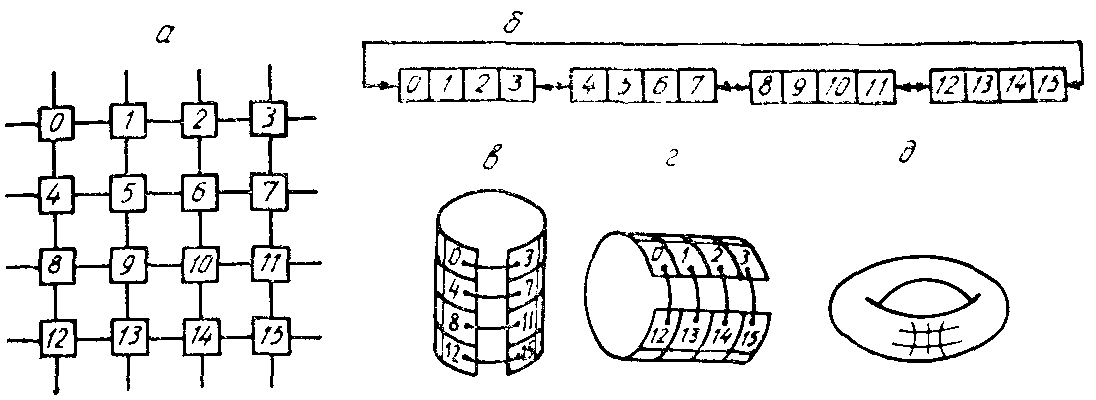
Рис. 11. Коммутатор с матричной схемой соединений

Быстродействие любого коммутатора во многом определяется максимальным расстоянием D, под которым понимается число промежуточных узлов или тактов передачи информации между самыми удаленными процессорами.

Под кубическим коммутатором понимается пространственная трехмерная структура, где каждый процессор соединен с шестью соседними: четырьмя в своей плоскости и двумя в прилегающих плоскостях.

В общем случае все среды можно назвать n-мерными кубами, тогда кольцевой коммутатор имеет размерность п=1, а матрица - п=2 и т. д. Большое распространение в параллельной вычислительной технике получили среды с размерностями 2 и 3. Чем больше п при неизменном числе процессоров, тем больше радиус связей и тем меньше D. Под радиусом связи понимается число процессоров, напрямую связанных с данным ПЭ.

Величина п может быть и больше трех. Покажем общий прием построения n-кубов произвольной размерности (рис. 2.28).

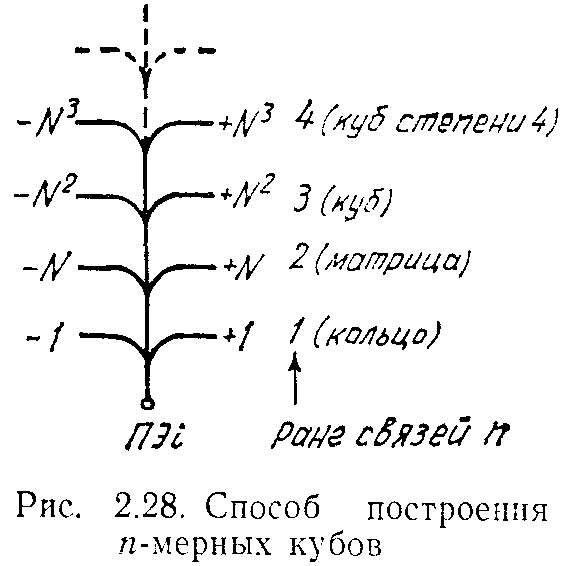
Для примера рассмотрим возможные связи элемента 9 матрицы, изображенной на рис. 11, а. Этот элемент в своей строке связан с элементами 8 и 10, адреса которых отличаются на -1 и +1. Если бы данная строка составляла независимый коммутатор с размерностью 4 (n=1, M=4), то связи любого ПЭi такого коммутатора описывались бы рангом 1. Если элемент 9 находится в матрице, то его связи с элементом 5 верхней строки и элементом 13 нижней строки отличаются на +M и -M, где M=4 - размер строки. Следовательно, связи элемента ПЭi матричного коммутатора описываются рангом 2 (см. рис. 2.28).

Если бы элемент 9 находился в кубе, то номера смежных элементов соседних плоскостей отличались бы на ±M², в кубе степени 4 - на ±M³ и т. д., что и показано на рис. 2.28. Такая методика позволяет построить куб любой степени и вычислить величину D.

Многокаскадные коммутаторы помогают создать более дешевые варианты соединительных и обобщенных соединительных сетей. Координатный переключатель nxn можно свести к двум (N/2XN/2) переключателям с замещением (рис. 13, а). В свою очередь переключатели N/2XN/2 могут быть разложены на более мелкие подобным же образом. Пример сети, приведенной до уровня стандартных 1<Э размерностью 2х2, дан на рис. 13, б. По определению, это полная соединительная сеть (сеть Бенеша), обеспечивающая N! возможных перестановок, каждая из которых выполняется за один такт работы сети. В такой сети отсутствуют конфликты для любых парных соединений.

Стандартный КЭ размерностью 2Х2 и возможные в нем соединения показаны на рис. 14. Иногда для построения больших сетей применяются элементы 4Х4 или 8Х8. Основной недостаток сети Бенеша - большое количество элементов, необходимых для ее построения.

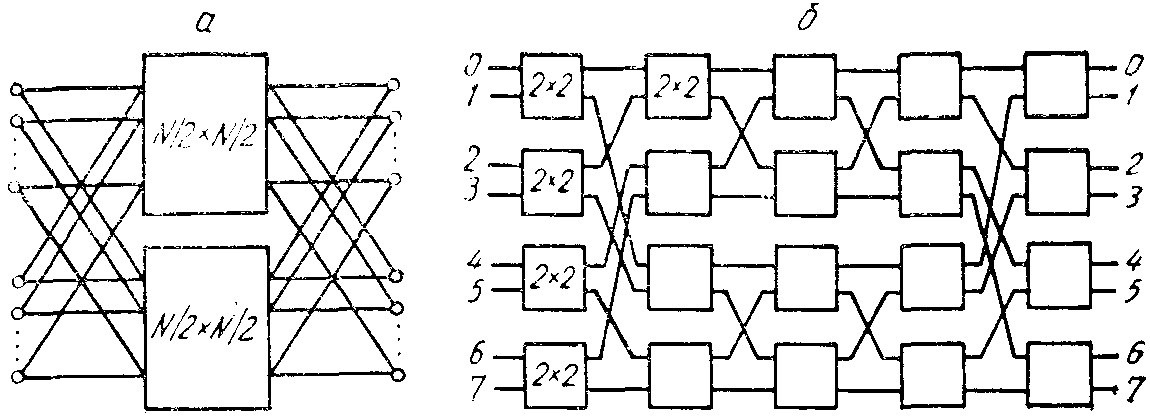
Рис. 13. Способ построения сети Бенеша

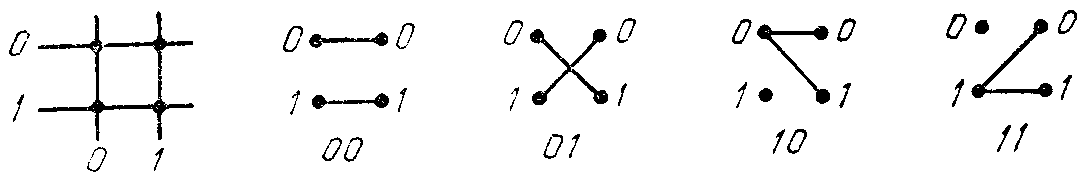
Рис. 14. Коммутационный элемент размерностью 2Х2 и допустимые перестановки.

Внизу приведены коды для нумерации перестановок

Широко используются неполные соединительные сети: омега-сеть, сеть Бенеша, R-сеть и др. Омега-сеть относится к типу сетей тасовки с замещением.

Коммутационные сети могут работать в двух режимах: коммутация каналов и коммутация сообщений. В первом случае сначала с помощью адресной системы устанавливается прямой электрический тракт между парой соединяемых точек, а затем по этому тракту передастся информация. Такой вид связи используется, например, в телефонных сетях. Во втором случае каждая передаваемая единица информации снабжается адресом требуемого выхода и перемещается от узла n_i, к узлу n_i+1, где i - номер каскада; п и т - номера коммутационных узлов в каскадах. После того как информация принята узлом m_i+1, линия, соединявшая n_i и m_i+1, становится доступной для других соединении. Узел m_i+1 по адресной части сообщения определяет дальнейший маршрут сообщения. В матрицах процессоров используется как коммутация каналов, так и коммутация сообщений.

Для описания сетей вводят некоторые обозначения. Пусть входы перестановочной сети обозначаются метками V₀, V₁, ..., V _L-1, а выходы - W₀, W₁, ..., W_L-1. При нумерации входов и выходов целыми чис­лами эти метки принимают значения, соответствующие их ин­дексам, т. е. Vo = 0, V₁ = 1, .... V_L-1 = L-1 и Wo = 0, W₁ = 1, .... W_L-1=L-1. Обозначим двоичные коды номеров входов и выходов сети l-компонентными двоичными векторами v = (v_l-1 v_l-2 ... v₀) и w = (w_l-1 w_l-2 ... w₀). Тогда множе­ства всех входных и выходных портов сети есть V = {V₀, V₁, … , V_L-1} и W = { W₀, W₁, … , W_L-1}, или в двоично-вектор­ной форме V = {v₀, v₁, … , v_L-1} и W = { w₀, w₁, … , w_L-1}.

Опишем перестановку, выполняемую двоичной перестано­вочной сетью как преобразование кодов v, т. е. W = V == {v₀, v₁, ... , v_L-1}. Так как общая перестановка является комби­нацией статических (S1) и динамических (Di) перестановок, то, например, для Омега-сети (рис. 8) можно записать

v_ = v(St₀Di₀St₁Di₁St₂Di₂)_,

или в общем виде

v_ = v(St₀Di₀St₁Di₁ … St_l-1Di_l-1)_ .

Перестановки, выполняемые базовыми и n-Куб-сетями, описываются выражениями

v_{базисные} = v(Di₀St₁Di₁St₂ … Di_l-1)_{базисные},

v_n-Куб = v(Di₀St₀Di₁St₁ … Di_l-1 St_l-1) _n-Куб .

При одинаковом управлении динами­ческие перестановки для всех трех сетей одинаковы. Поэтому, чтобы сравнить работу перестановочных сетей, необходимо раскрыть содержание статических перестановок. Преобразова­ние vSt имеет связь с перестановками типа полной тасовки, получившими свое название от того, что перестановка выпол­няется посредством разрезания одного набора на два и чередо­ванием их элементов как при полной тасовке карт (рис. 15).

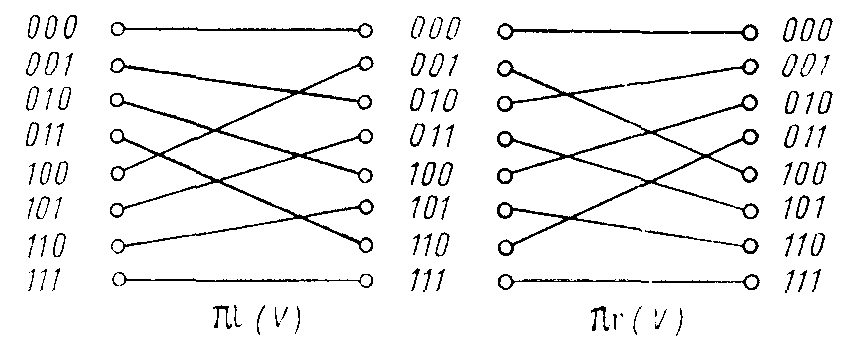
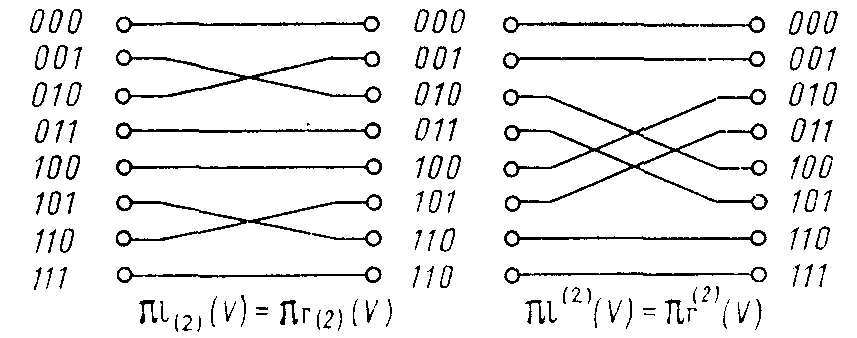
Рис. 15. Перестановки типа полной тасовки.

Еще несколько перестановок этого типа: k-я левая (l_(k)) и правая (r_(k)) подтасовки и k-я ле­вая (l^(k)) и правая (r^(k)) надтасовки, которые могут быть охарактери­зованы циклическими сдвигами влево и вправо младших и старших разрядов двоичного представления V_v.

В Омега-сети в качестве статических перестановок на всех ярусах используется перестановка полной тасовки , а в базисной сети - правая подтасовка при k = l-v, где v - номер яруса. В n-Куб-сети перестановка пол­ной тасовки выполняется на последнем ярусе, а на всех предыдущих статические перестановки описываются несколько другим выражением выраже­нием.

Описания перестановок, вы­полняемых Омега-, базисными- и n-Куб-сетями, различаются только порядком разрядов двоичных векторов и могут быть легко приве­дены друг к другу. Это значит, что, зная управляющий вектор для одной сети, мы можем выполнить такую перестановку на другой сети, переставив соответствующим образом разряды вектора управления и перенумеровав входы.

Применение перестановоч­ных сетей в параллельной памяти требует параллельного вы­полнения коммутаций (перестановок) для всех L входов. Одни из вариантов такой работы сети получится, если принять, что все КЭ одного яруса имеют общее управление, т. е. управля­ются одним сигналом c_v. Тогда, такое управление сетью будем называть поярусным.

При поярусном управлении n-Куб-сеть может ре­ализовать всего 2^l различных перестановок. В то же время в l-ярусной сети l * 2^l-1 коммутационных элементов, поэтому при раздельном управлении число различных коммутаций сети составит 2^k, где k=l*2^l-1. В таком случае управление сетью значительно усложняется. В связи с этим встает вопрос об анализе и синтезе перестановок для заданной сети.

Будем рассматривать перестановки, выполняемые над L элементами за один проход сети. Любая перестановка будет допустима, если она требует для каждого КЭ сети единствен­ного управляющего сигнала, т. е. если не возникает конфлик­тов при управлении КЭ. Приведем описание указанного условия для n-Куб-сети.

Возьмем любой КЭ нулевого яруса. Пара линий, подходя­щих к нему, различаются по номеру (адресу) только в одном младшем разряде двоичного представления. Выходы также различаются только младшим разрядом. Причем, если этот раз­ряд не изменился на КЭ нулевого яруса, то он уже нe может измениться на остальных КЭ сети. Например, если после нулевого яруса рассматривать верхний выход КЭ, которому соответствует значение 0 в младшем разряде номера линии, то после прохождения всей сети эта линия может быть скоммутирована только на те выходы сети, в которых младший разряд двоичного представления номера выхода w₀ = 0, что легко

_

проверить, по схеме на рис. 10. Поэтому, если номера входных линий КЭ нулевого яруса обозначить (v₃v₂v₁v₀) и (v₃v₂v₁v₀), то номе­ра

__

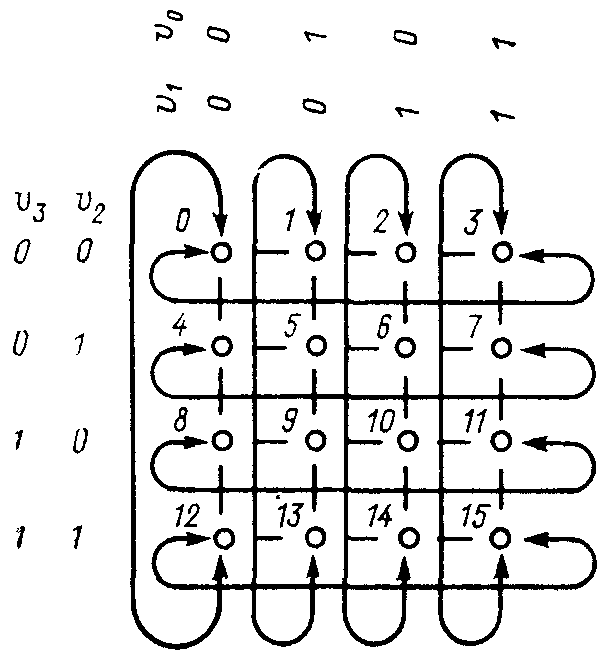
выходов КЭ можно обозначить (v₃v₂v₁w₀) и (v₃v₂v₁w₀). Соответственно, после прохождения второго яруса получим уже две неизменяемые компоненты в двоичном коде номера линии w₁ и w₀ и т. д. Отсюда следует вывод, что коммутационный эле­мент может полностью идентифицироваться (l—1) компонен­тами кодов номеров линий, входящих в него. В рассматривае­мом примере (рис. 10) для нулевого яруса это v₃v₂v₁, для первого - v₃v₂w₀, для второго - v₃w₁w₀ и для третьего – w₂w₁w₀.

Управляющие сигналы для всех коммутационных элементов сети будем представлять матрицей l X L/2. Элемент матрицы c_ij = 0,1 определяет состояние управляющего сигнала для j-го КЭ в i-м ярусе:

Строки матрицы делятся на равные группы. Число элемен­тов в группе для i-й строки равно 2ⁱ. Так, в нулевой строке в каждой группе 2⁰ элементов, в первой – 2¹ и т. д. Пример де­ления на группы для матрицы 4 X 8, соответствующей сети на рис. 10, приведен на рис. 16. Управляющие сигналы во всех группах одной строки совпадают, что предопределяет схему их разводки. Так, в нулевой строке группа состоит из одного элемента, и, значит, элементы нулевой строки либо все равны 0, либо 1. Это равносильно тому, что все управляющие сигналы нулевого яруса могут быть объединены вместе. В первой стро­ке матрицы группа включает два элемента. Следовательно, 4х8 управляющая матрица 16-входовой n-Куб-сети в первой строке содержит четыре группы, и общими являются управляющие сигналы 0-, 2-, 4- и 6-го КЭ и 1-, 3-, 5- и 7-го КЭ. Соответственно ко второму ярусу КЭ должны подходить 4 управляющих сиг пала, а к третьему - восемь.

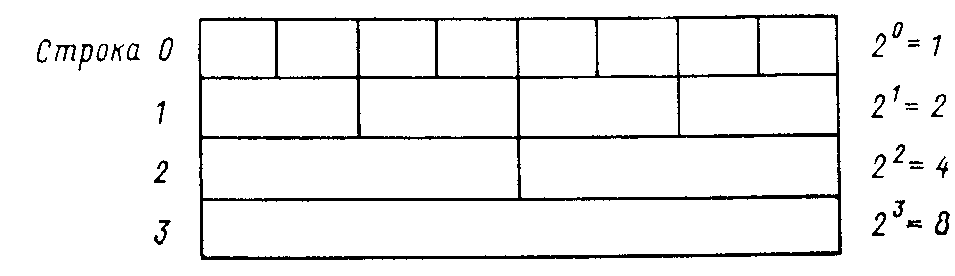
Рис. 16. Пример деления матрицы управляющих сигналов на группы.

Управляющие сигналы и каждой группе формируются по коду счетчика Джонсона.

Таким образом, если формируется матрица управляющих сигналов для выполнения на n-Куб-сети циклического сдвига вход­ной последовательности на v позиций, то для каждой строки код в соответствующих группах определяется по представле­нию v в коде Джонсона.

Ниже приведены матрицы управляющих сигналов для реа­лизации линейных циклических сдвигов (ЛЦС) на n-Куб-сети с 16 входами. Матрицы даны для реализации сдвигов вправо. Чис­ла в скобках указывают величину сдвига. Ввиду цикличности сдвигов переход к сдвигам влево не представляет труда:

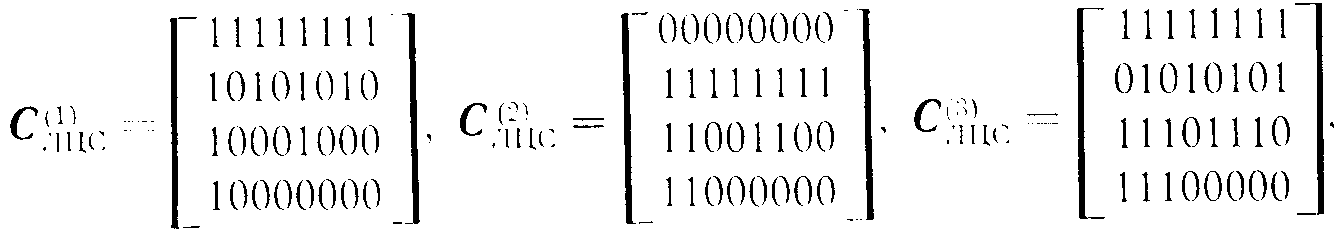
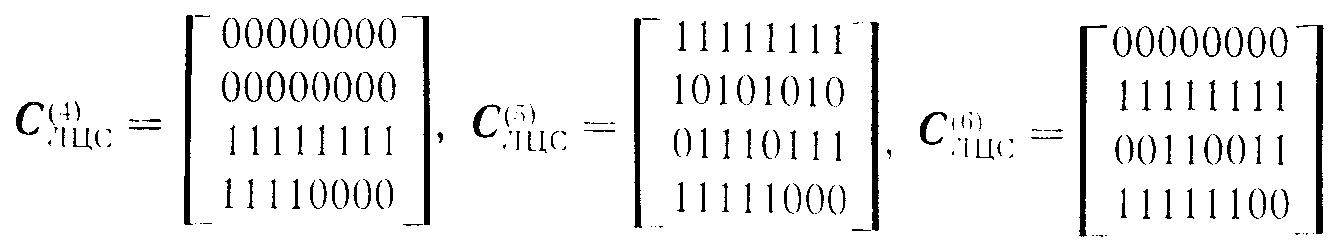
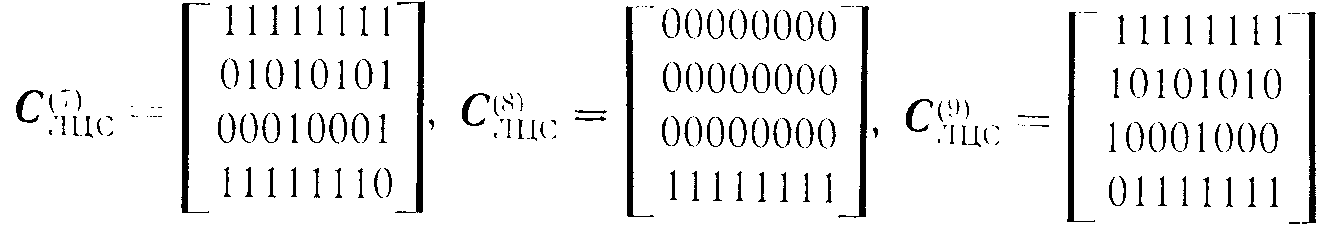
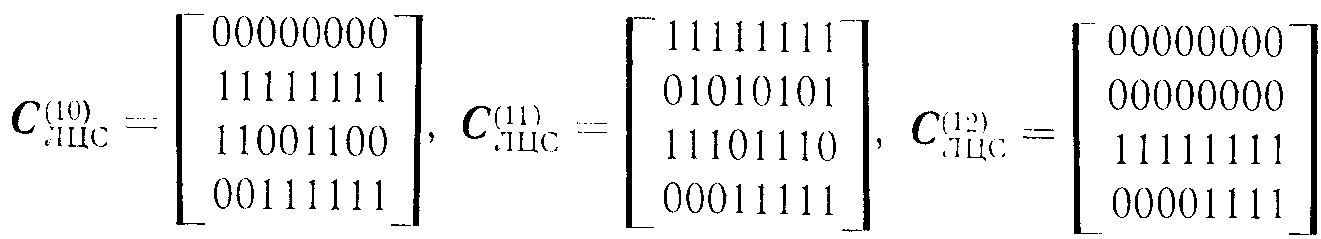
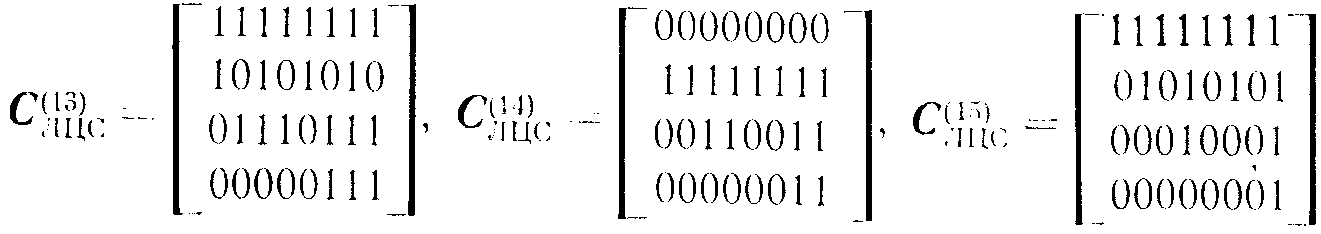
Еще одна интересная возможность управления n-Куб-сетью за­ключается в том, что циклический сдвиг можно производить над отдельными группами входов.

Управляющие матрицы мож­но получить из уже известных, выбирая только те строки, ко­торые относятся к соответствующим ярусам, и формируя из них новую матрицу. Так, для сдвига по строкам необходимо ис­пользовать две верхние строки матриц С⁽¹⁾_ЛЦС, С⁽²⁾_ЛЦС и С⁽³⁾_ЛЦС, а для сдвига по столбцам - две нижние строки матриц С⁽⁴⁾_ЛЦС, С⁽⁸⁾_ЛЦС и С⁽¹²⁾_ЛЦС . Таким образом легко формируются матрицы управляющих сигналов для реализации двухмерного сдвига. В 6oлее общем случае можно рассматривать p-мерные структуры и соответствующие им p-мерные сдвиги.

Если обеспечить не общее, а групповое управление коммутационными элементами на младших ярусах, то число комбинаций циклических сдвигов можно еще расширить. Из схемы сети (рис. 10) видно, что каждая группа из четырех входов на первых двух ярусах никак не связана с другими. Значит, при соответст­вующем управлении для каждом строки структуры (рис. 17) можно выполнять свой сдвиг. То же самое можно сказать и в отношении групп КЭ двух старших ярусов, реализующих сдвиги столбцов.

Таким образом двоичные перестановочные сети обладают двумя весьма ценными качествами: простотой и ши­рокими возможностями реали­зации параллельных перестано­вок на основе диадных и линейных циклических сдвигов. Диадные сдвиги очень просто реализуются при поярусном управлении сетью. Выполнение линейных циклических сдвигов требует несколько более сложного управления.

Рис. 17. Иллюстрация линейных циклических сдвигов на двухмер­ной решетке

Используемая литература:

1. Метлицкий Е.А., Каверзнев В.В. Системы параллельной памяти. Теория, проектирование, применение. Л. Издательство ГУ. 1989.

2. Шпаковский Г.И. Архитектура параллельных ЭВМ. Минск. «Университетское». 1989.

2