
Литература по которой Горячев читает лекции / Часть 2. ВС с одиночным потоком команд / 2.3. Процессорные матрицы / Сети коммутаци1
.docсети коммутации
Введение
Сети коммутации представляют основу проекта процессорной матрицы и построение их очень важно для эффективного использования матриц. По этой причине мы посвятили целый раздел этому компоненту архитектуры процессорной матрицы. Сети коммутации также представляют собой важную часть в архитектуре вычислительных машин и связи, особенно если учесть сильную склонность к распределенным вычислительным системам. Однако мы попытаемся представить этот предмет, осветив преимущественно вопросы применения взаимосвязей процессорных матриц и последующую обработку данных. В отношении подробностей по другим применениям и современной библиографии читатель может обратиться к обзорной статье.

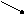








 В 0
В 0




 х 1
х 1

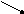




 о 2
о 2




 д 3
д 3


 ы
ы
0 1 2 3
Выходы
а) а)









 0
0
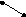






 В 1
В
В 1
В
х ы
о х




 д 2
о
д 2
о


 ы
д
ы
д

 ы
ы
 3
3

в) в)
Рис. 3.11. Все возможные отображения Рис. 3.12. Два представления координатного
трех входов на два выхода: переключателя на четыре входа и четыре
а) один ко многим; в) один к одному выхода
Сети коммуникации представляют множество взаимосвязей или отображений между двумя наборами узлов, входами и выходами. Для N входов и M выходов существуют N! четко определяемых отображений от входов до выходов, где под термином «четко определяемый» мы подразумеваем, что каждый выход определяется одним и только одним входом. На рис. 3.11 изображены четко определяемые отображения между тремя входами и двумя выходами. Сеть, выполняющая все NM таких отображений, мы будем называть обобщенной соединительной сетью (GCN).
Если мы ограничимся классом отображений один к одному, то будут существовать N! четко определяемых таких отображений. На рис. 3.11 также показан поднабор отображений один к одному; они передают данные от одного входа только на один выход. Чтобы такие отображения не были пустыми, для этого класса должно быть, по крайней мере, столько же входов, сколько и выходов. Сеть, которая выполняет эти N! отображений, мы будем называть соединительной сетью (CN).
Наиболее очевидный способ реализации обобщенной соединительной сети – это создание так называемой полной или завершенной координатной сети, где каждый вход может быть коммутирован на любой выход. Это иллюстрируется с помощью двух представлений на рис. 3.12. На первом отображении (рис. 3.12, а) ребра представляют наборы входов и выходов, а узлы – пересечения или коммутаторы. Альтернативное представление дается с помощью двудольного графа (рис. 3.12, б), где узлы представляют множество входов и выходов, а ребра – пересечения. Полное пересечение представляет собой общую форму сети коммуникации, хотя число необходимых точек пересечений равно NM, поскольку между каждым входом и выходом требуется одна точка пересечения. Поэтому при большом N эта сеть становится очень дорогой. В процессорных матрицах практическим ограничением для N является значение 24 или 25, тогда как число процессоров может достигать 214 или более. Сети такого рода использовались в проекте BSP фирмы Burroughs – одна с N = 16 и M = 17, другая с M =16 и N =17.
Другие сети коммуникации базируются либо на многочисленных малых взаимосвязанных координатных сетях, либо на неполных координатных сетях. О них разговор пойдет несколько позже; вначале мы должны представить нотацию и определить некоторые перестановки, которые существенно упростят рассмотрение.
Некоторые основные перестановки
Перестановка упорядоченного набора из N узлов определяется функцией (x), где x и (x) - целые числа в диапазоне 0 x, (x) N1. Функция (x) также должна быть взаимно-однозначной. Например, функция
() (x) = [x/2]2 + ||x|2 + 2-1|2
определяет перестановку с замещением (рис. 3.13).
Полагают, что наиболее простой способ охарактеризовать перестановки – это рассмотреть двоичное представление x. Таким образом,
x = {bn, bn-1,…,b1} = bn 2n-1 + bn-1 2n-2 + … + b1
представляет двоичный адрес элемента в наборе. Перестановки набора входов теперь можно обозначить посредством операций или перестановок их двоичных адресов. Эта нотация дает хороший результат, и использовалась в некоторых докладах, связанных с вопросами обработки данных и маршрутизации сетей.
Перестановка с замещением. Указанная выше перестановка с замещением сейчас может быть более просто определена в двоичном представлении x:
() (x) = {bn,…,b,…, b1}. (3.11)
Черта обозначает дополнение данного бита. Следовательно, -я перестановка с замещением определяется дополнением -го разряда двоичного представления x.
Перестановки типа полной тасовки. Название «полная тасовка» происходит от того, что перестановка выполняется посредством разрезания одного набора на два и чередования этих двух наборов как при полной тасовке карт (рис. 3.14). Эта перестановка соответствует устройству циклического сдвига влево двоичного представления x:
0

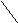








 00
000
000 000
00
000
000 000
0








 01
001
001 001
01
001
001 001
0







 10
010
010 010
10
010
010 010
0






 11
011
011 011
11
011
011 011
1







 00
100
100 100
00
100
100 100
1






 01
101
101 101
01
101
101 101
1





 10
110
110 110
10
110
110 110
1




 11
111
111 111
11
111
111 111
(1) (2) (3)
Рис. 3.13. Перестановки с замещением
000 000 000 000






 001
001 001
001
001
001 001
001






 010
010 010
010
010
010 010
010





 011
011 011
011
011
011 011
011


 100
100 100
100
100
100 100
100



 101
101 101
101
101
101 101
101


 110
110 110
110
110
110 110
110


 111
111 111
111
111
111 111
111
(2) (2)
Рис. 3.14. Перестановки с полной тасовкой
(x) = {bn-1, bn-2,…, b1, bn}. (3.12)
-я перестановка подтасовки () и -я перестановка надтасовки () могут быть также охарактеризованы циклическими сдвигами влево наименьших и наибольших разрядов соответственно:
() (x) = {bn,…, b+1, b-1,…, b1, b}, (3.13)
() (x) = {bn-1,…, bn-+1, bn, bn-,…, b1}. (3.14)
Они иллюстрируются на рис. 3.14 для n = 3 и k = 2. Ясно, что
(n) (x) = (n) (x) = (x), (1) (x) = (1) (x) = x.
На рис. 3.14 можно видеть, что при подтасовке (наименьших значащих разрядах) набор рассматривается, как ряд поднаборов, выполняющих полную тасовку в каждом поднаборе. Несмотря на то, что при надтасовках тасуется весь набор, полоса тасуемых данных увеличивается.
Перестановка типа «бабочка» (рис. 3.15) характеризуется двоичным представлением х с перестановкой последнего и первого бита:
(х) = {b1, bn-1,…, b2, bn}. (3.15)


 000
000 000
000
000
000 000
000




 001
001 001
001
001
001 001
001






 010
010 010
010
010
010 010
010






 011
011 011
011
011
011 011
011


 100
100 100
100
100
100 100
100






 101
101 101
101
101
101 101
101


 110
110 110
110
110
110 110
110


 111
111 111
111
111
111 111
111
= (2) = (2) (2) = (2)
а) в)
Рис. 3.15. Перестановка типа «бабочка» (а) и разрядно – реверсивные (в)



 0
0 0
0
0
0 0
0

 1
1 1
1
1
1 1
1

 2
2 2
2
2
2 2
2

 3
3 3
3
3
3 3
3


 4
4 4
4
4
4 4
4

 5
5 5
5
5
5 5
5

 6
6 6
6
6
6 6
6
7 7 7 7
(2) (2)
Рис. 3.16. Перестановки со смещением
Как и при тасовке, мы можем обозначить -ю подбабочку и -ю надбабочку х. В -й подбабочке меняется -й и первый разряды, а в -й надбабочке – n-й и (n - + 1)-й разряды:
() (х) = {bn,…, b+1, b1, b-1,…, b}, (3.16)
() (x) = {bn-+1,…, bn-+2, bn, bn-,…, b1}. (3.17)
Примеры под- и надбабочек приведены на рис. 3.15 для n = 3 и = 2. И опять:
(n) (x) = (n) (x) = (x), (1) (x) = (1) (x) = x.
Разрядно - реверсивная перестановка, как можно судить по названию, характеризуется изменением порядка разрядов на обратный в двоичном представлении х:
(х) = {b1, b2,…, bn}. (3.18)
Одно из применений, где встречается данная перестановка, - алгоритм быстрого преобразования Фурье (см. разд. 5.5).
Как и в предыдущих двух перестановках, -я подразрядная и -я надразрядная инверсии могут быть обозначены также наименьшими и наибольшими значащими разрядами величины х:
() (x) = {bn,…, b+1, b1, b2,…, b}, (3.19)
() (x) = {bn-+1, bn-+2,…, bn, bn-,…, b1}. (3.20)
На рис. 3.15 иллюстрируется разрядная инверсия для n = 3. Однако, как это будет показано далее, когда мы будем рассматривать алгебру перестановок, две перестановки не всегда являются эквивалентными.
Перестановка со смещением. Эта последняя перестановка характеризуется весьма просто, не прибегая к разрядному представлению х:
(x) = |x+1| n . (3.21)
2
Снова определим под- и надсдвиги наименьших и наибольших значащих разрядов двоичного представления значения х. В переводе на разрядное представление х уравнение (3.21) обозначает двоичное сложение над n-разрядным полем без учета переполнения. Поэтому под- и надсдвиги можно обозначить как
() (х) = |х + 1| , (3.22)
2
() (х) = |х + 2n-| n . (3.23)
2
Это иллюстрируется на рис. 3.16 для n = 3 и =2.
