Частинні похідні і повні диференціали вищих порядків

Нехай функція z= f(x;y) має частинні похідні в усіх точках множини D . Візьмемо будь-яку точку (х; y)є D; в цій точці існують частинні похі­дні і , які залежать від х і у, тобто вони є функції двох змінних.

Значить, можна ставити питання про знаходження їх частинних похідних. Якщо вони існують, то називаються похідними другого порядку і познача­ють відповідно або (читаємо: де два зет по де ікс квадрат),

або , або ,

а бо .

Аналогічно визначаються і позначаються частинні похідні третього і вищих порядків, на­приклад:

Означення: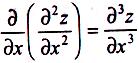 Диференціалом другого порядку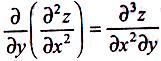

від функції z = f(x,y) на­зивається диференціал від її повного диференціалу, тобто

Аналогічно визначаються диференціали третього і вищих порядків

……………………………………………………………………….

Приклад 1: Знайти , якщо z= sinx · siny

Приклад 2: Знайти для функції

Приклад 3: Знайти і для функції

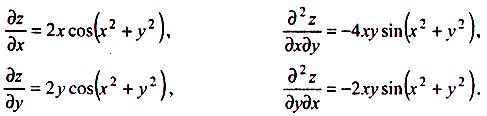
У попередньому прикладі ми одержали, що . Виявляється,

що ця рівність має місце в досить значному числі випадків, що випливає із наступної теореми.

Теорема : Якщо функція z = f(x,y) визначена в області D, в цій області існують перші похідні f_x' і f_y' , другі змішані похідні і і похідні як функції від х і у неперервні в точці (x₀; y₀) , тоді в

цій точці

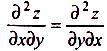
Похідна неявної функції

Неявна функція

Означення : Функція називається явною, якщо її задано рівнянням, права частина якого не містить залежної змінної у, тобто формулою _y=f(x) . Наприклад, явними є функції: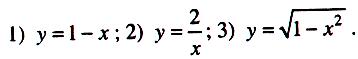

Функція у від аргументу х називається неявною, якщо її задано рів­няням , яке не є розв'язаним відносно залежної змінної.

(1)

Отже, маємо ще один спосіб задання функції.

У такому випадку кажуть, що функцію задано неявно, або в неявному вигляді. Наприклад, неявними є функції:

Для того щоб подати функцію у, яку задано рівнянням (1), у явному вигляді, досить це рівняння розв'язати відносно у. Якщо, наприклад, розв'язати рівняння 4) - 6) відносно у, то дістанемо, відповідно, явні функції 1) - 3).

Проте не завжди вдається розв'язати рівняння (1) відносно у. На­приклад, рівняння 7) розв'язати відносно у важко. У такому випадку функцію у доводиться вивчати, користуючись безпосередньо рівнянням, яке її задає.

Сукупність значень аргументу x, для кожного з яких рівняння (1) має хоча б один дійсний корінь у, складає область існування неявної функції. Зауважимо, що не кожне рівняння (1) визначає неявну функцію. Наприклад, рівняння

(2)

очевидно, не визначає ніякої функції.

Рівняння

(3)

яке записується без додаткових умов, також не визначає функції. Справді, оскільки то кожному хє(-1;1) відповідає два значення y.

Геометрично це можна тлумачити так: графіком рівняння (3) є коло ра­діуса r = 1 з центром у початку координат. Будь-яка пряма, паралельна осі ординат у смузі буде перетинати коло у двох точках. Отже, лінія, яка визначається рівнянням (1), не є графіком функції. З цього становища можна вийти, наклавши додаткову умову, наприклад, у>0.

Тоді рівняння задаватиме функцію у неявному

вигляді.

Означення : Якщо існує неперервна функція однієї змінної y= f(x) така, що відповідні пари (x;y) задовольняють умову F(x; у), тоді ця умова називається неявною формою функції f(x), сама функція f(x) називається неявною функцією, яка задовольняє умову F(x; y)= 0.

Припустимо, що неперервна функція y= f(x) задана в неявній формі

F(x,y) = 0 і що F_y '(x;y) ≠ 0 .Похідна знаходиться за формулою

Приклад 1: Знайти похідну від неявної функції в точці х = 1, у = 2 .

• Маємо , , звідки

Для х = 1, у = 2 маємо

Аналогічно частинні похідні функції двох незалежних змінних , яка задана за допомогою рівняння , де — диференційо-

вна функція змінних х, у, z , можуть бути обчислені за формулами

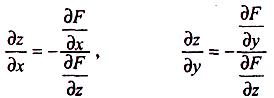(1)

за умови, що

Приклад 2: Знайти , якщо

• В даному випадку . Знайдемо

Тоді за формулами (1)

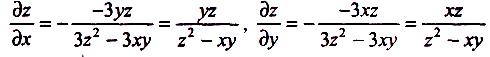
Приклад 3: Знайти повний диференціал функції двох змінних:

z= arctg .

• Знайдемо

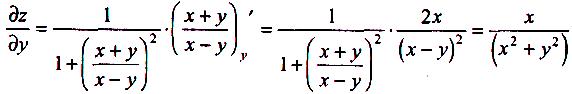
Отже,

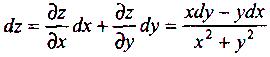
Приклад 4: Знайти _dz, якщо _xyz=x+y+z

• Якщо відомо, ,

отже, спочатку знайдемо

Функція . Тоді

За формулами (1) маємо

Отже,

ДОСЛІДЖЕННЯ ФУНКЦІЇ ДВОХ ЗМІННИХ

Екстремум функції двох змінних

Означення: Нехай функція z= f(x;y) визначена в деякому околі точки і неперервна в цій точці. Якщо для всіх точок цього околу ви-

конується нерівність , тоді ця точка

називається точкою максимуму (мінімуму) функції z= f(x;y)

Точки максимуму й мінімуму називаються точками екстремуму.

Теорема (необхідна умова екстремуму):

Якщо функція z = f(x; у) має екстремум у точці (х_о,у_о), тоді в цій точці частинні похідні або дорівнюють нулю, або хоча б одна з них не існує.

Теорема (достатня умова для екстремуму):

Нехай функція z = f(x; у) має екстремум у точці (х_о,у_о) неперервні частинні похідні пер­шого й другого порядку, причому , а також Якщо:

1) тоді (х_о,у_о) точка максимуму функції z = f(x; у);

2) тоді (х_о,у_о) точка мінімуму функції z = f(x; у);

3) тоді в точці (х_о,у_о) немає екстремуму.

4) тоді потрібні додаткові дослідження.

Алгоритм дослідження функції z = f(x; у) на екстремум

1. Знайти перші частинні похідні

2. Знайти стаціонарні точки, тобто точки, в яких

3. Знайти частинні похідні другого порядку

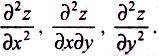
4. Обчислити значення частинних похідних другого порядку в стаціо­нарних точках.

5. Для кожної стаціонарної точки знайти (дискримінант)і зробити ви­сновки згідно теореми про достатню умову існування екстремуму.

6. Записати відповідь.

Приклад: Розглянемо функцію Обчислимо

2. Необхідна умова існування екстремуму в тому, що

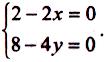
Розв'язком цієї системи є точка х = 1, у = 1. Таким чином, в точці (1; 2) функція може мати екстремум.

3. Знайдемо похідні другого порядку , , звідки одержуємо, що Δ =( -2) · (-4) − 0= 8 .

4. Як випливає з пункту 5 алгоритму знаходження екстремуму — екст­ремум існує. Це максимум, бо А < 0.