Неперервність функції двох змінних

Означення: Функція називається неперервною в точці

, якщо

Означення: Функція називається неперервною в області

(замкненій чи відкритій), якщо вона неперервна в кожній точці цієї області.

Приклад: Розглянемо функцію двох незалежних змінних

Ця функція має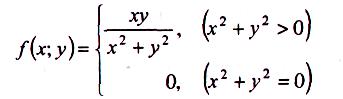 розрив у точці , бо в цій точці для функції границі не існує .

Тут ми зустрічаємось із цікавим явищем. Функція, що розглядається, не є неперервною в точці (0;0) по двом змінним водночас, але є неперервною

по змінним х та у окремо.

Приклад: точки розриву можуть бути не тільки ізольованими, як у попе­редньому прикладі, а й заповнювати лінії, поверхні і т. п.

Так, функції двох

змінних , мають розриви:

перша − прямі , друга — окіл

Для функції трьох змінних ,

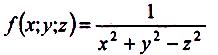
розриви заповнюють у першому випадку гіперболічний параболоїд

, а в другому — конус

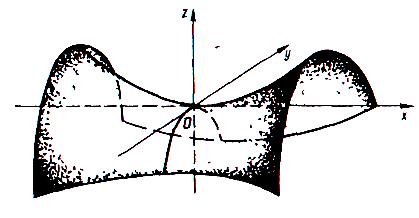
Зауваження

Гіперболічний параболоїд.

Гіпербо­лічним параболоїдом називається поверх­ня, що задана рівнянням

Таку поверхню називають іноді сідлоподібною поверхнею.

ДИФЕРЕНЦІЙОВНІСТЬ ФУНКЦІЇ ДВОХ ЗМІННИХ

Часткові та повний прирости функції двох змінних

Нехай функція визначена в деякому околі точки

Надамо незалежним змінним х та у приріст та так, щоб точка

не виходила за межі вказаного окола. Тоді й точки , також виявляються в околі, що розглядається (мал. 1).

Означення: Різницю f(x₀+Δ x; y₀+ Δy)- f(x₀; y₀) називають повним приростом функції при переході від точки (x₀; y₀) до точки (x₀+Δ x; y₀+ Δy) і позначають Δz .

Різницю називають частковим приростом по х,

а різни­цю — частковим приростом по y функції ; їх позначають відповідно . Таким чином, ­

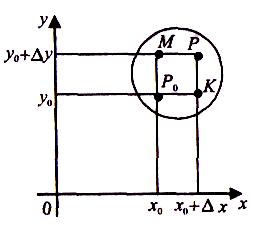
Мал. 1

Зауваження: Аналогічно визначаються прирости функції більш ніж двох змінних.

Диференційовність функції двох змінних

Означення: Функція z= f(x;y) називається диференційовною у точці (x₀; y₀), якщо її повний приріст можливо подати у вигляді:

де — числа,— нескінченно малі при,

Означення: Головна лінійна частина приросту функції , тобто називається повним диференціалом функції (точніше першим диференціалом) f(x;y) у точці (x₀; y₀), і позначається: dz

Теорема : Якщо функція z= f(x;y) диференційовна в точці (х₀,у₀), тоді існують границі

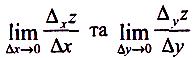
Означення: Нехай функція z= f(x;y) визначена в точці (x₀; y₀) і в її

деякому околу. Якщо існує , то вона називається час-

тинною похідною по х (по у) функції z= f(x;y) в точці(x₀; y₀) і познача-

ється , або , або

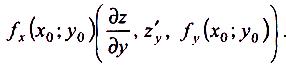
Приклад: Знайти для функції z = x³y + sin(x² + )+

+ tg x + ln у .

• Знайдемо . Вважаючи, що y= const, одержимо:

При знаходженні вважаємо, що х = const. Одержимо:

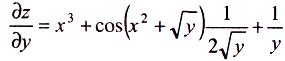
Диференціали незалежних змінних збігаються з їх приростами:

dx = Δх, dy = Δy.

Повний диференціал функції z = f(x; у) обчислюється за формулою

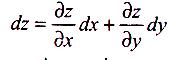
Аналогічно повний диференціал функції трьох аргументів и = f(x;y;z) обчислюється за формулою

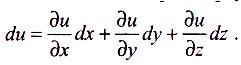
Приклад: Знайти du , якщо

•

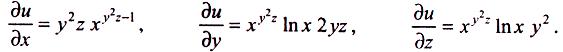
Отже,

Достатня умова диференційовності функції двох змінних у точці.

Для функції однієї змінної диференційовність та існування похідної є рівнозначними твердженнями. У випадку функції двох змінних ми маємо інше: існування частинних похідних — необхідна умова диференційовнос­ті функції в точці, але не є достатньою умовою диференційовності: напри­клад, для функції

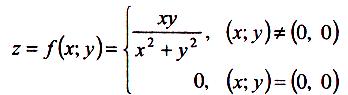
в точці (0, 0): . Але ця функція розривна в точці (0, 0), а то-

му функція не може бути диференційовною в цій точці.

Таким чином, для диференційовності функції z = f(x;y) в точці (х_о;у_о) недостатньо тільки існування частинних похідних і диференційовність має місце, якщо додат­ково вимагати неперервність частинних похідних, що випливає з поданої нижче теореми.

Теорема : Якщо функція z = f(x;y) в деякому околу точки (х_о;у_о)

має неперервні частинні похідні, тоді вона диференційовна в точці (х₀ ;у₀)