С т а т и к а корабля модуль 5.7
3.13. Динамическая остойчивость. Плечо динамической остойчивости
На судно могут действовать не только статические кренящие моменты, но и динамические, приложенные резко (качка, шквал, рывок буксирного троса и т.д.). В этом случае судно получает запас не только потенциальной энергии, но и кинетической. Вся приложенная к судну энергия должна компенсироваться работой восстанавливающего момента, т.е. судно должно обладать динамической остойчивостью, если же не компенсируется, судно будет динамически неостойчивым.
Рассмотрим подробнее процесс наклонения судна. Можно считать, что в центре величины погруженной части судна приложена равнодействующая сил поддержания, поэтому точку С можно рассматривать как точку опоры плавающего судна. Тогда работа, произведенная при наклонении, будет зависеть от изменения вертикального расстояния между центром тяжести и центром величины (точкой опоры), т.е. работа будет производиться при подъеме веса D над центром величины. Она будет равна
T=Dd , (1)
где d - изменение расстояния по высоте между ЦТ и ЦВ, или иначе, плечо динамической остойчивости.
С другой стороны, работу восстанавливающего момента можно определить как
(2)
Приравняем (1) и (2) . Тогда получим
и
,
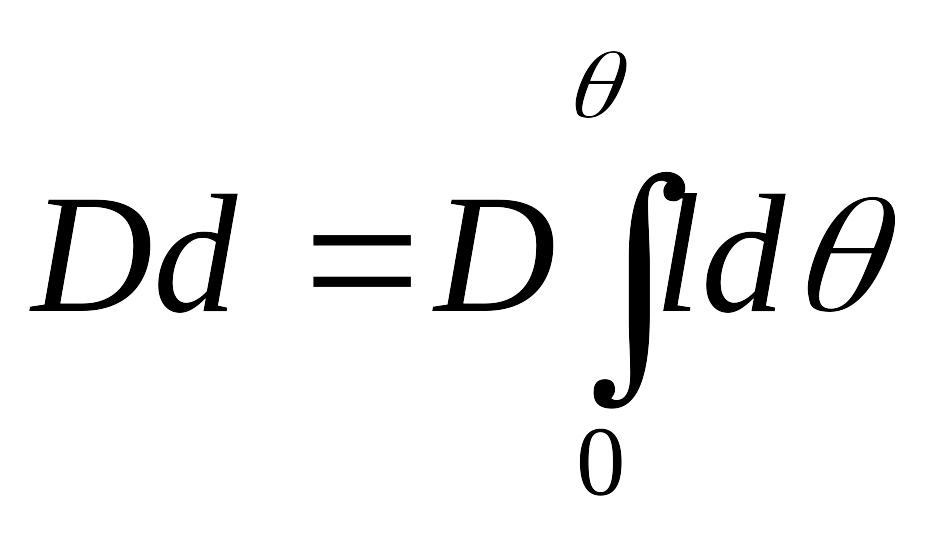
(3)
т.е. плечо динамической остойчивости равно определенному интегралу от плеча статической остойчивости.
Из формулы (3) следует, что
(4)
и
.
(5)
Величину
d
можно получить также графически (рис.1
), если от точки К
отложить по линии
величину а.
Тогда расстояние
будет характеризовать изменение
расстояния по высоте между ЦТ и
ЦВ, т. е.
По
построению
,
где
.
Окончательно:
.
(6)
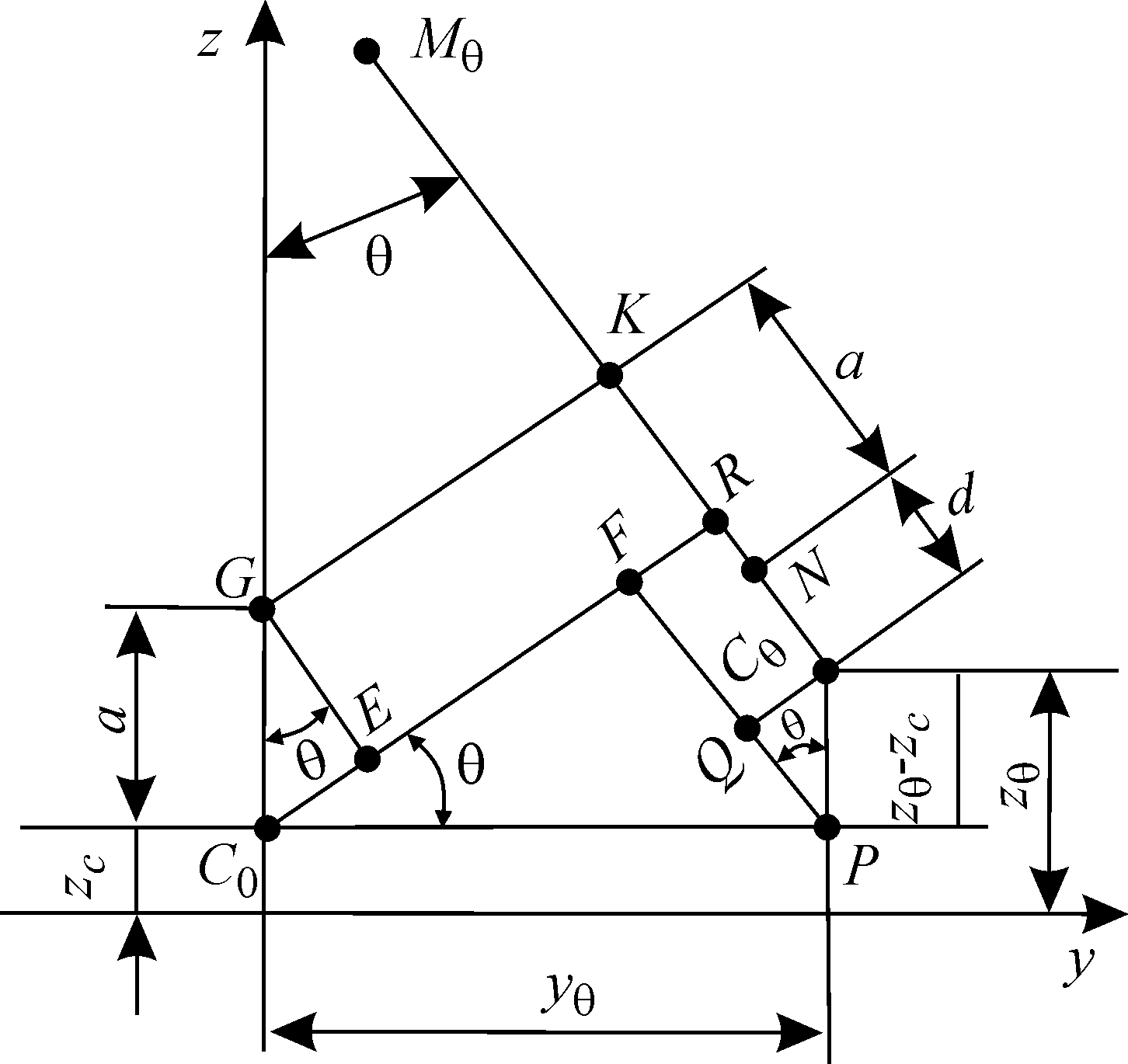
Рис.1
Если построить кривую d (θ), получится диаграмма динамической остойчивости, связанная с диаграммой статической остойчивости интегральной зависимостью (рис.2). Если на диаграмме динамической остойчивости провести при угле θ касательную к кривой d и отложитъ по горизонтали 1 рад, получится плечо статической остойчивости l, соответствующее углу θ (рис.3)
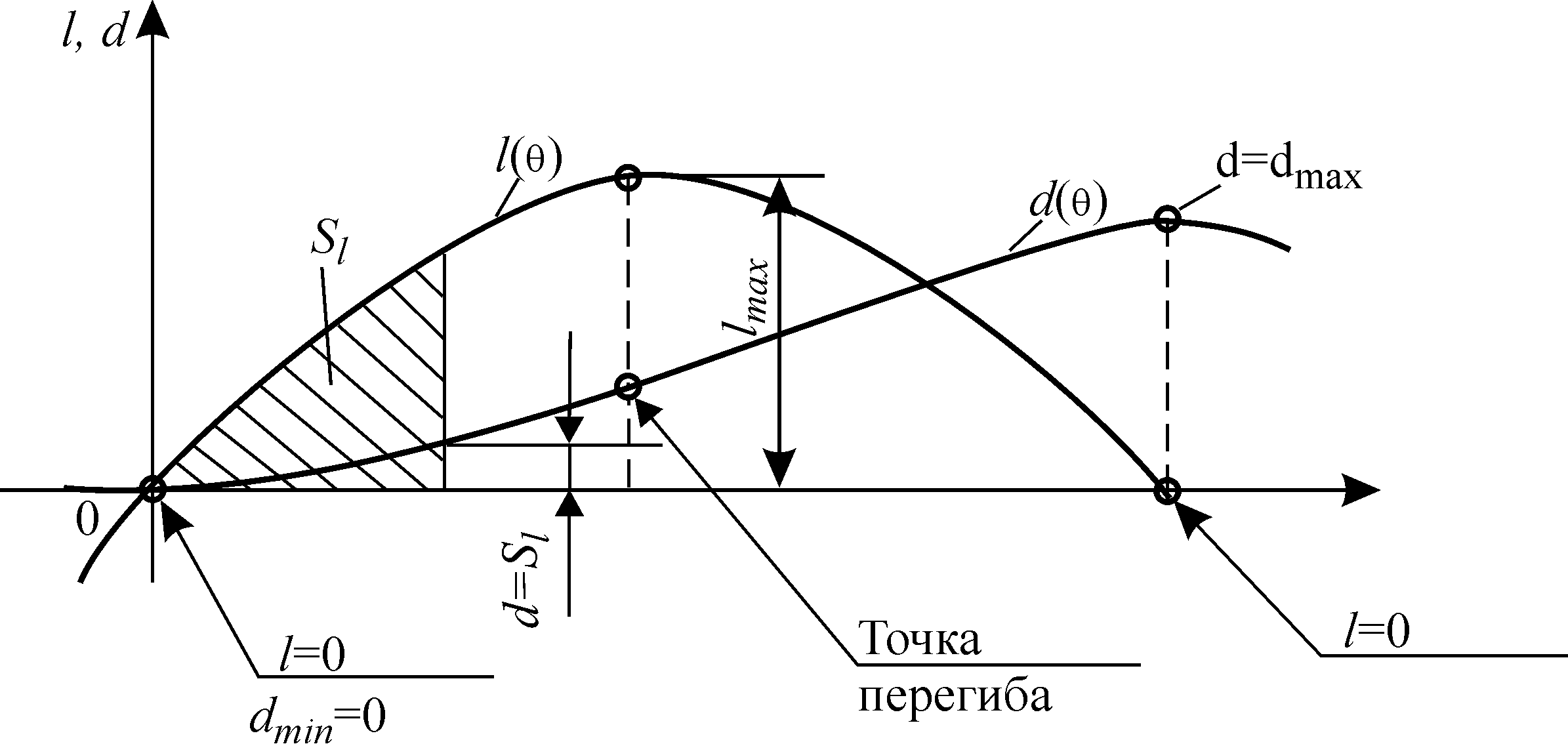
Рис.2.Диаграммы динамической и статической остойчивости при поло-жительной h0
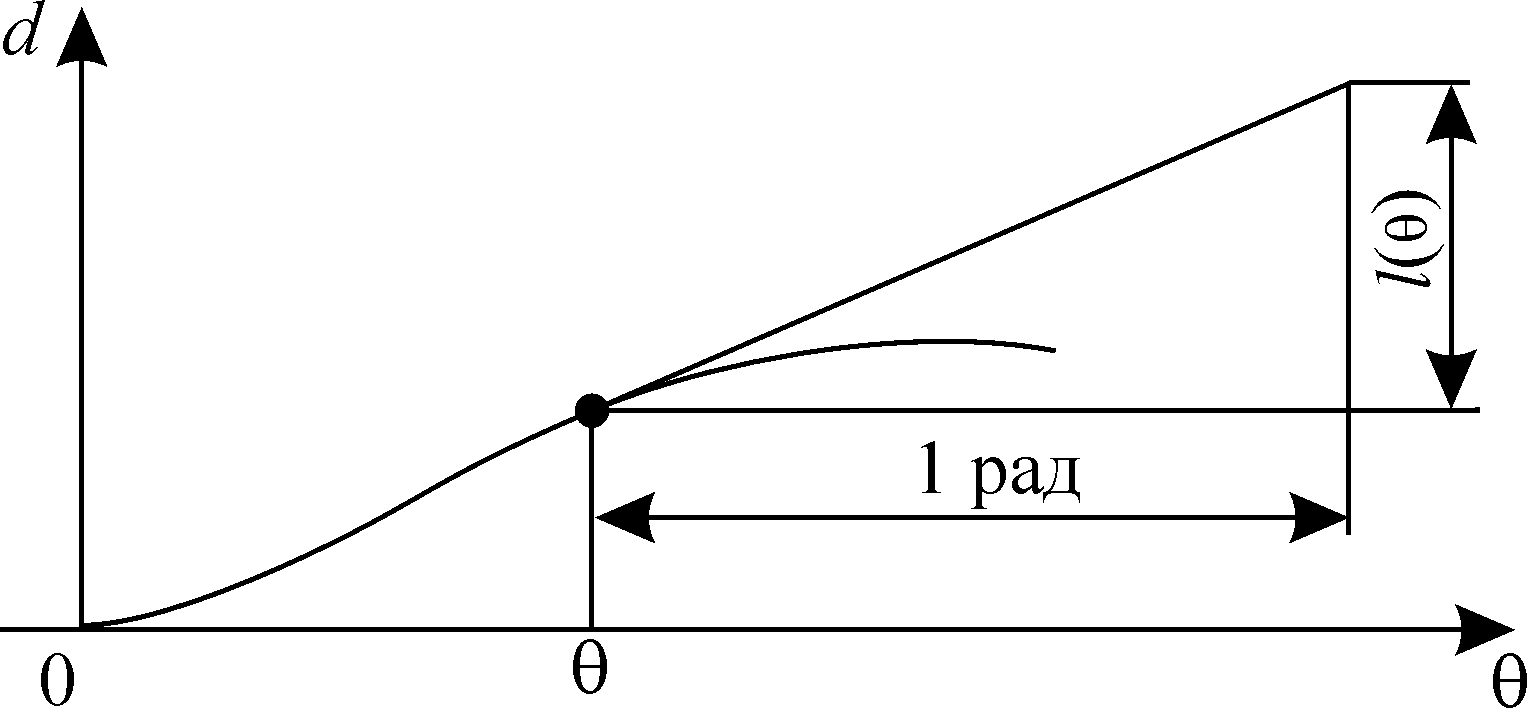
Рис.3. Определение 1(θ) по диаграмме динамической остойчивости