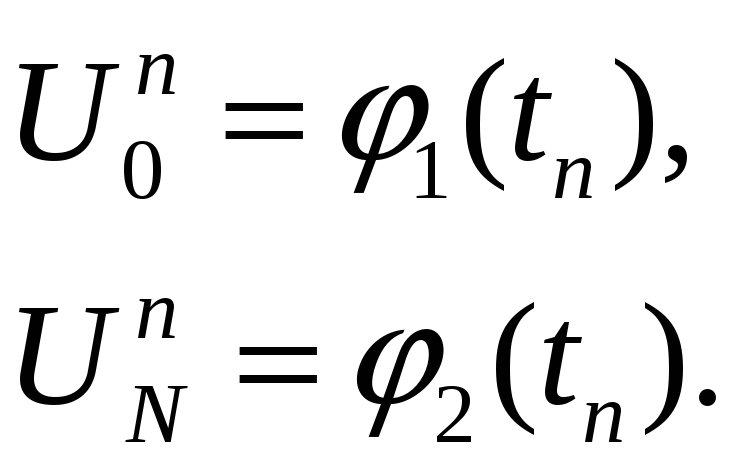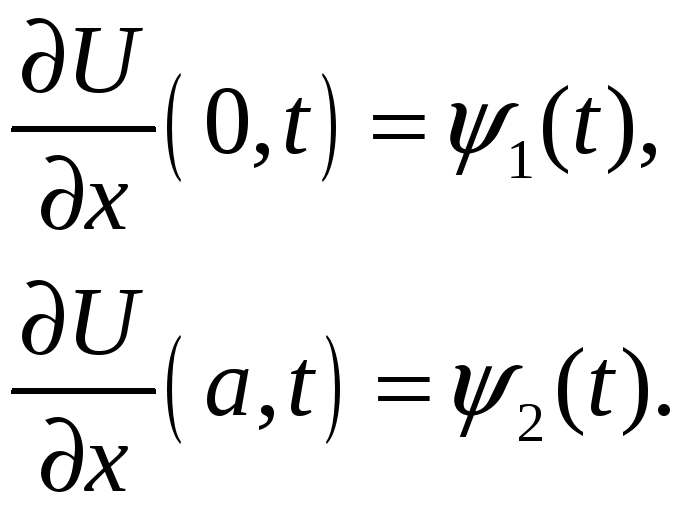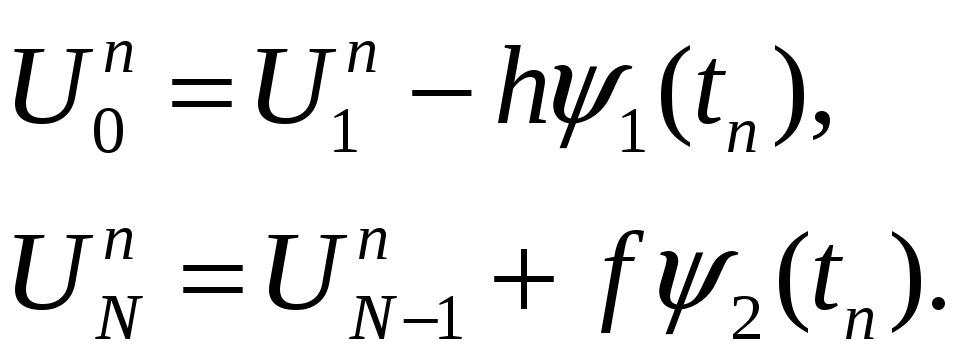4.2. Нелинейное уравнение теплопроводности

Пример 1. Автомодельное решение типа "тепловой фронт"

Намного более интересные решения можно получить для нелинейного уравнения теплопроводности, например, с нелинейным источником тепла . Если задать его в таком виде, то получится решение в форме тепловых фронтов, распространяющихся в обе стороны от зоны первичного нагрева (рис.4.5). 

Пример 2. S-режим горения "с обострением"

Еще более неожиданные решения возможны при нелинейности также и коэффициента диффузии. Например, если взять , а , то можно наблюдать эффект горения среды, локализованный в области ее первичного нагрева (рис.4.6). На рис.4.6 показаны 5,6,7 шаги по времени – температура за конечное время обращается в бесконечность. Это так называемый S-режим горения "с обострением". Предлагается поэкспериментировать с этим и другими нелинейными вариантами уравнения теплопроводности. Существенно, что такие интересные результаты удается получить лишь численно. 

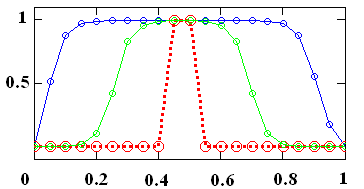
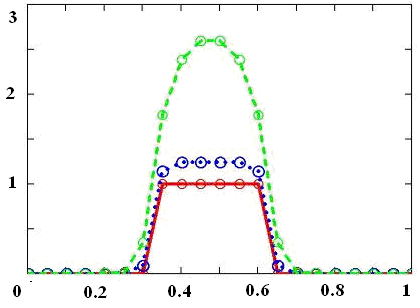
Рис.4.5. Автомодельное решение типа "тепловой фронт" для нелинейного уравнения с источником .	Рис.4.6 Автомодельное решение типа "тепловой фронт" (режим с обострением).

Задание

1. Используя явную схему (4.3), численно решить линейное уравнение (4.1)

2. Сравните расчеты по неявной схеме с расчетами по явной схеме Эйлера.

3. Используя явную схему Эйлера, численно решить уравнение (1) с нелинейным источником тепла .

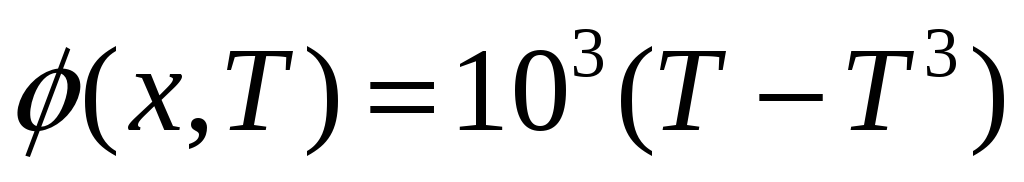4. Для наблюдения эффекта горения среды, локализованного в области ее первичного нагрева с нелинейным источником тепла, численно решить уравнение (1) с коэффициентом диффузии 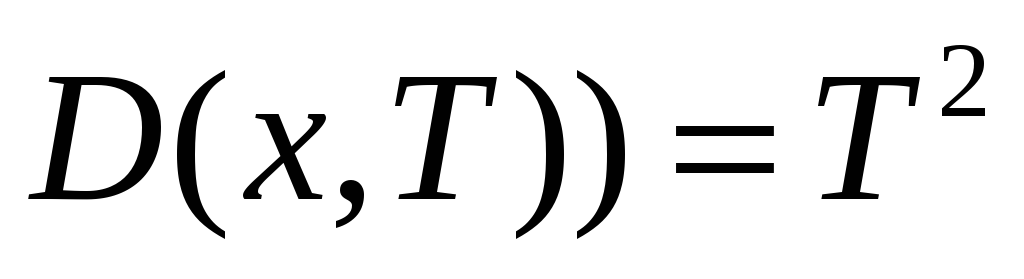и источником 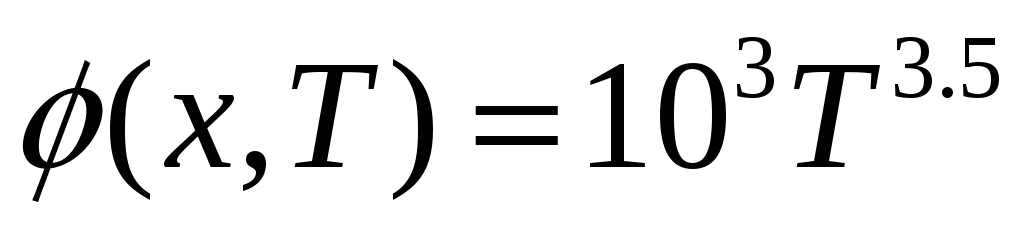. Использовать явную схему Эйлера.

5. Волновое уравнение

Волновое уравнение гиперболического типа

.

(5.1)

описывает одномерные линейные волны без дисперсии. Например, колебания струны_, звук в жидкости (газе) или электромагнитные волны в вакууме (в последнем случае уравнение (5.1) должно быть записано в векторном виде).

Общее решение уравнения (5.1) представим в виде

,

(5.2)

где функции f и g определяются из начальных и граничных условий:

	(5.3)
	(5.4)

Решение (5.2) описывает две волны, бегущие в противоположные стороны с постоянной и одинаковой скоростью с без изменения своей формы.

Простейшей разностной схемой, аппроксимирующей уравнение (5.1), является явная пятиточечная схема

,

(5.5)

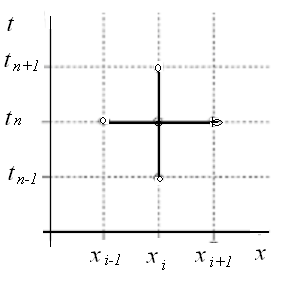
шаблон которой показан на рис.5.1. Эта схема, получившая название «крест», имеет второй порядок точности по времени и по пространственной координате и является трехслойной по времени. Ее применение предполагает, что при нахождении значений на верхнем слое значения и уже известны. Для начала расчетов по этой схеме требуется задать значения и . Значения определяются сразу из первого начального условия (5.3)

(5.6)

Значения можно определить лишь приближенно из второго начального условия (5.3):

.

(5.7)

Граничные условия (5.4) аппроксимируются без труда

(5.8)

Таким образом, задача (5.1), (5.3), (5.4) аппроксимируется уравнениями (5.5) (5.8). Область устойчивости схемы «крест» ограничена условием Куранта–Фридрихса-Леви [5-7]

.		(5.9)
Примечание. Граничные условия II рода (5.10) С погрешностью аппрокcимируютcя уравнениями: (5.11)	Рис.5.1 Шаблон схемы «крест» для волнового уравнения.
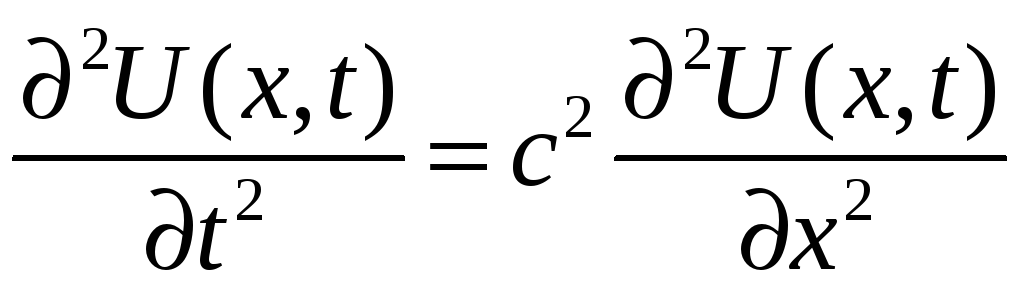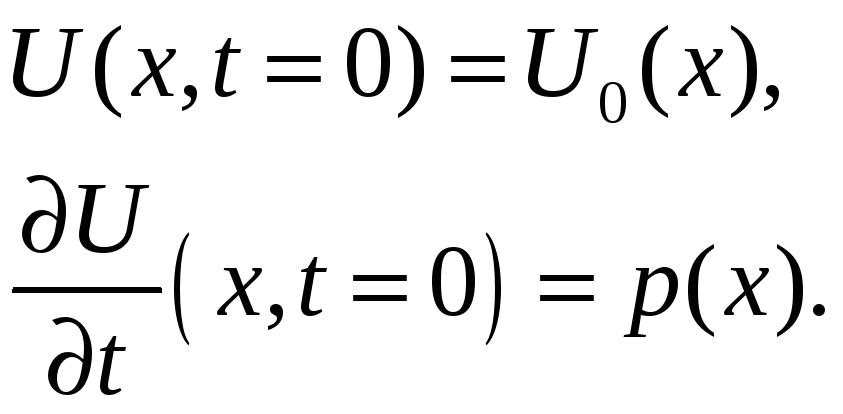
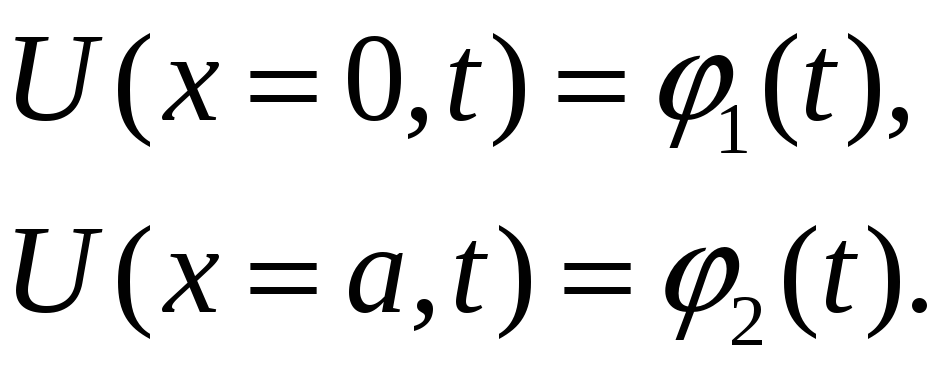
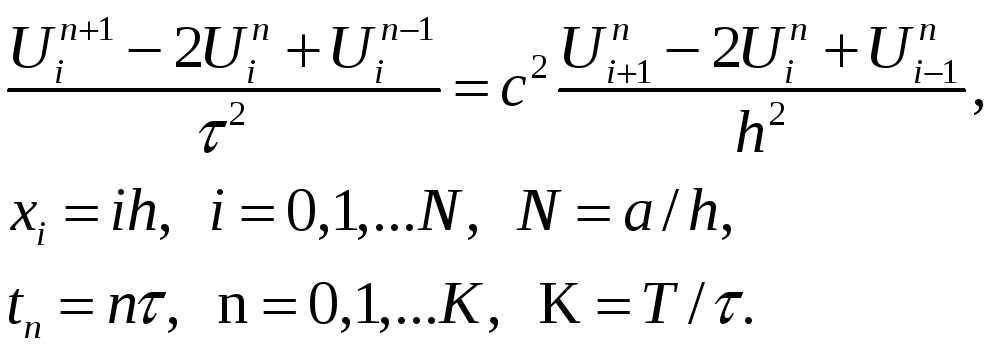