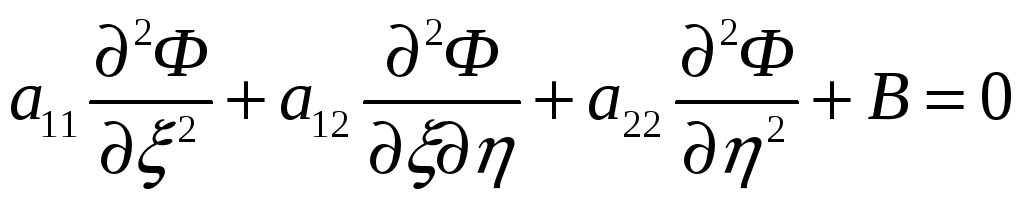В.А.Михайлова

Е.А.Михайлова

КОМПЬЮТЕРНОЕ МОДЕЛИРОВАНИЕ

ЭВОЛЮЦИОННЫХ УРАВНЕНИЙ

МИНИСТЕРСТВО НАУКИ И ОБРАЗОВАНИЯ РФ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

ВОЛГОГРАДСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

Физико-технический институт

Кафедра теоретической физики и волновых процессов

В.А. Михайлова, е.А. Михайлова

КОМПЬЮТЕРНОЕ МОДЕЛИРОВАНИЕ ЭВОЛЮЦИОННЫХ УРАВНЕНИЙ

УЧЕБНО-МЕТОДИЧЕСКОЕ ПОСОБИЕ

для студентов направлений подготовки магистров 03.04.02 «Физика»

профили подготовки:

«Физика. Информационные процессы и системы»,

«Физика. Физика конденсированного состояния вещества»,

«Астрофизика. Физика космических излучений и космоса».

Волгоград 2014

УДК ББК	536.75 22.317 М69 Печатается по решению редакционно-издательского совета Волгоградского государственного совета
	Рецензенты д. физ.-мат. наук, профессор С.В. Феськов
М69	Учебное пособие по курсу «Компьютерное моделирование эволюционных уравнений» [Текст]: для студентов направления подготовки магистров 03.04.02«Физика» / В.А Михайлова, Е.А. Михайлова ФТИ, каф. ТФ и ВП. – Волгоград: Изд-во ВолГУ, 2014. – 24с. ISBN Учебно-методическое пособие содержит лабораторные работы и предназначено для проведения компьютерного практикума в объеме не менее 24 часов аудиторной работы. Предназначено для студентов направления подготовки магистров 03.04.02 «Физика», ВолГУ. ББК
ISBN	© В.А Михайлова, Е.А. Михайлова 2014

«Уравнения для меня важнее, потому что политика — для настоящего, а уравнения — для вечности.» Альберт Эйнштейн

ВВЕДЕНИЕ

Эволюционные уравнения - уравнения, описывающие процессы, протекающие во времени, например, распространение тепла, распространение волн. Эволюционное уравнение - уравнение, допускающее истолкование как запись дифференциального закона развития (эволюции) во времени некоторого процесса. Термин не имеет точного определения, и его применимость может зависеть не только от самого уравнения, но и от постановки задачи для него. Для эволюционного уравнения характерна возможность построения решения при заданном начальном условии, которое трактуется как запись начального состояния процесса. К эволюционным уравнениям относятся, прежде всего, обыкновенные дифференциальные уравнения и их системы общего вида

(*)

т. п. в случае, когда естественно рассматривать как решение задачи Коши. Эти уравнения (*) описывают эволюцию систем с конечным числом степеней свободы.

Многие задачи физики сводятся к интегрированию уравнений в частных производных. Эти уравнения возникают при моделировании физических полей, например электромагнитных.

Типы уравнений в частных производных.

Дифференциальные уравнение с частными производными 1-го порядка, называется квазилинейным, если оно линейно относительно производных 1-го порядка от неизвестной функции Ф.

Рассмотрим квазилинейные уравнения с частными производными 2 порядка с двумя независимыми переменными [1 - 3].

(**)

где a_ij, B, - заданные непрерывно дифференцируемые функции от , ,. (a₁₂ )² – a₁₁a₂₂ =- дискриминант уравнения (**).

1. Если >0 - уравнение (**) гиперболического типа;

2. Если =0 - уравнение (**) параболического типа;

3. Если <0 - уравнение (**) эллиптического типа.

Примеры:

Уравнение теплопроводности

( = t, = x ) , a₁₁ = a₁₂ = 0, a₂₂ = - , a₁₁a₂₂ = 0 – уравнение параболического типа.

Волновое уравнение

( = t², = x² ), a₁₁ = 1, a₁₂ = 0, a₂₂ = - c² , a₁₁a₂₂ < 0 - уравнение гиперболического типа.

Уравнение Пуассона

( = t², = x² ) , a₁₁ = 1, a₁₂ = 0, a₂₂ = 1 , a₁₁a₂₂ > 0 - уравнение эллиптического типа.