
- •В.А. Михайлова, е.А. Михайлова
- •1. Движение заряженных частиц в электромагнит- ном поле.
- •1.1 Движение в однородном магнитном поле
- •1.2. Движение заряженных частиц в комбинированных полях
- •Задание
- •2.Фазовые портреты динамических систем
- •Задание
- •3. Уравнение переноса
- •Задание
- •4. Уравнение теплопроводности
- •4.2. Нелинейное уравнение теплопроводности
- •Задание
- •5. Волновое уравнение
- •Задание
- •Список литературы
- •Содержание
Задание
-
Численно решить смешанную задачу Коши для нелинейного уравнения переноса (3.5) с начальным условием
 и левым
граничным условием
и левым
граничным условием
 (Нелинейный перенос с поглощением). Для
численного решения уравнения переноса
применить явную разностную схему (3.2).
Использовать равномерную сетку (ось
(Нелинейный перенос с поглощением). Для
численного решения уравнения переноса
применить явную разностную схему (3.2).
Использовать равномерную сетку (ось
 )
на отрезке [0,1] с шагом dx.
)
на отрезке [0,1] с шагом dx. -
Численно решить смешанную задачу Коши – уравнение (3. 6) с начальным условием
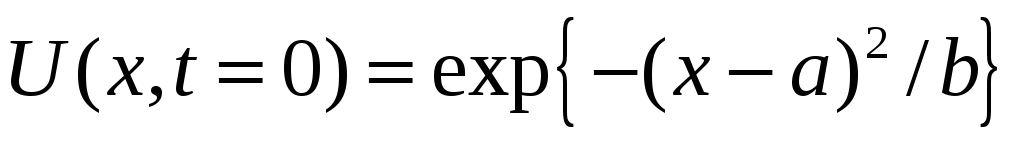 и левым
граничным условием
и левым
граничным условием
 (уравнение Бюргерса).
(уравнение Бюргерса).
4. Уравнение теплопроводности
Дифференциальное уравнение теплопроводности (или уравнение диффузии тепла) записывается следующим образом:
|
|
(4.1) |
Это уравнение
параболического
типа, содержащее первую производную по
времени t
и вторую по пространственной координате
x.
Оно описывает динамику температуры
![]() например,
остывающего или нагреваемого металлического
стержня (функция T
описывает профиль температуры по
координате
х вдоль
стержня). Коэффициент D называется
коэффициентом теплопроводности
(диффузии). Он может быть как постоянным,
так и зависеть, как явно от координат,
так и от самой искомой функции D(t,
x,T). Если
данная зависимость является нелинейной,
то нелинейным становится и само уравнение,
что приводит к характерным его решениям.
Функция
например,
остывающего или нагреваемого металлического
стержня (функция T
описывает профиль температуры по
координате
х вдоль
стержня). Коэффициент D называется
коэффициентом теплопроводности
(диффузии). Он может быть как постоянным,
так и зависеть, как явно от координат,
так и от самой искомой функции D(t,
x,T). Если
данная зависимость является нелинейной,
то нелинейным становится и само уравнение,
что приводит к характерным его решениям.
Функция
![]() описывает распределение источников
тепла вдоль стержня, а также их зависимость
от температуры. Опять-таки, если
описывает распределение источников
тепла вдоль стержня, а также их зависимость
от температуры. Опять-таки, если
![]() зависит от
зависит от
![]() нелинейно, нелинейным становится и само
уравнение.
нелинейно, нелинейным становится и само
уравнение.
4.1. Линейное
уравнение теплопроводности
описывается дифференциальным уравнением
в частных производных (4.1), в котором
коэффициент диффузии D и источники тепла
![]() не зависят от температуры
не зависят от температуры
![]() .
Исследуем численно линейное уравнение
с постоянным коэффициентом диффузии
D=const и
в условиях отсутствия источников тепла,
т.е.
.
Исследуем численно линейное уравнение
с постоянным коэффициентом диффузии
D=const и
в условиях отсутствия источников тепла,
т.е.
![]() =0.
Начальные и граничные условия задают
начальный нагрев центральной области
стержня и поддержание постоянной
температуры на его краях соответственно.
Для решения уравнений типа диффузии
(теплопроводности) применяют как явные,
так и неявные разностные схемы. Последние
требуют решения на каждом временном
шаге СЛАУ, которая часто оказывается
трех диагональной (поэтому возможно ее
решение методом прогонки). Явная схема
для простейшего уравнения теплопроводности
устойчива при соблюдении условия
Куранта
на шаги по времени и пространству:
=0.
Начальные и граничные условия задают
начальный нагрев центральной области
стержня и поддержание постоянной
температуры на его краях соответственно.
Для решения уравнений типа диффузии
(теплопроводности) применяют как явные,
так и неявные разностные схемы. Последние
требуют решения на каждом временном
шаге СЛАУ, которая часто оказывается
трех диагональной (поэтому возможно ее
решение методом прогонки). Явная схема
для простейшего уравнения теплопроводности
устойчива при соблюдении условия
Куранта
на шаги по времени и пространству:
|
|
(4.2) |
Решение линейного уравнения (4.1), описывающее распределение температуры вдоль остывающего стержня (от x=0 до 1) в момент времени t (D=1, =0) с начальным распределением, представленным на рис.4.1, с физической точки зрения вполне ожидаемо - с течением времени тепло из более нагретой области перетекает в менее нагретую, а зона изначально высокой температуры остывает и размывается. Ниже приведены несколько примеров использования явной схемы Эйлера для расчета линейного уравнения теплопроводности (4.1). Шаг по времени τ=0.0005, число точек по оси х М=20, дискретизация начального условия по сетке =1/M=0.05. На рис.4.2 изображено начальное распределение температуры и её динамика через 1, 10 и 20 шагов по времени соответственно. Условие Куранта выполнено, поэтому схема устойчива. Физически такое поведение вполне естественно - с течением времени тепло из более нагретой области перетекает в менее нагретую, а зона изначально высокой температуры остывает и размывается.
|
|
|
|
Рис.
4.1. Начальное
распределение температуры
|
Рис.4.2. Численное решение линейного уравнения (4.1)
|
Решение (рис.4.2) получено численно с использованием явной схемы, шаблон которой показан на рис.4.3.
|
|
|
|
Рис.4.3. Шаблон явной схемы |
Рис. 4.4 Шаблон неявной схемы |
Разностная аппроксимация дифференциального уравнения (4.1) в соответствии с шаблоном (рис.4.3):
|
|
(4.3) |
Выписанные
равенства определяют (N-1)M линейных
алгебраических уравнений относительно
(N+1)(M+1) неизвестных чисел
![]() (искомых
значений функции в узлах сетки). Еще M+1
равенств дадут начальные условия для
(искомых
значений функции в узлах сетки). Еще M+1
равенств дадут начальные условия для
![]() и еще 2N равенств дадут граничные условия
для
и еще 2N равенств дадут граничные условия
для
![]() .
Уравнения образуют разностную явную
схему Эйлера. Решение этой системы
уравнений очень просто, т.к., зная
.
Уравнения образуют разностную явную
схему Эйлера. Решение этой системы
уравнений очень просто, т.к., зная
![]() для можно
явно выразить через них искомые
для можно
явно выразить через них искомые
![]() (на следующем шаге по времени). Можно
показать, что явная разностная схема
Эйлера для задачи диффузии является
устойчивой, если соотношение Куранта
меньше 1. Если же оно превышает 1, то
разностная схема неустойчива, и ее ответ
неверен.
(на следующем шаге по времени). Можно
показать, что явная разностная схема
Эйлера для задачи диффузии является
устойчивой, если соотношение Куранта
меньше 1. Если же оно превышает 1, то
разностная схема неустойчива, и ее ответ
неверен.
Решим теперь линейное уравнение теплопроводности, при помощи неявной схемы Эйлера, шаблон которой представлен на рис.4.4. Заменяем на сетке исходное дифференциальное уравнение (4.1) его разностной аппроксимацией в соответствии с шаблоном (рис.4.4):
|
|
(4.4) |
Теперь надо выразить
искомые значения на следующем шаге по
времени (временном слое)
![]() через
через
![]() .
Полученная система уравнений будет
линейной относительно искомых
.
Полученная система уравнений будет
линейной относительно искомых
![]() ,
для решения которой удобно использовать
метод прогонки [5].
,
для решения которой удобно использовать
метод прогонки [5].

 .
.



 .
. .
.