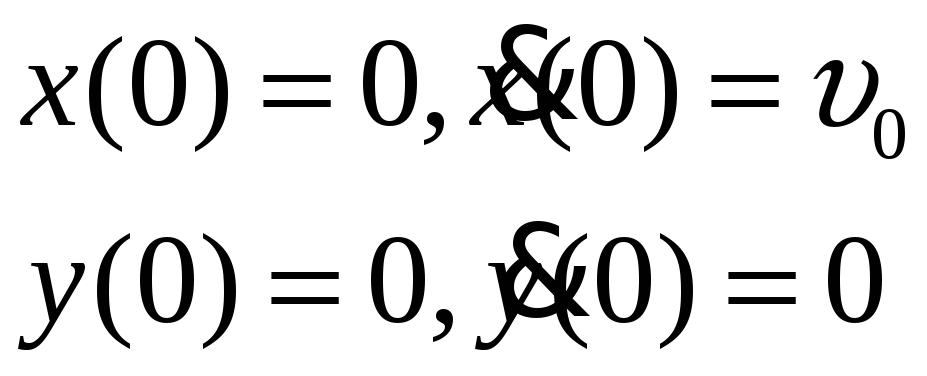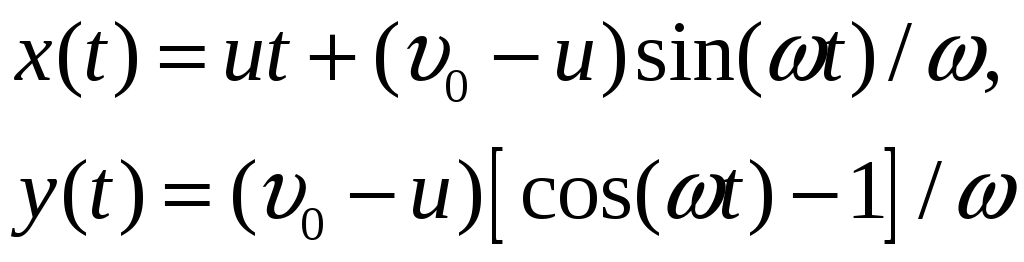1.2. Движение заряженных частиц в комбинированных полях

Пусть направление электрического и магнитного полей совпадают. Ориентируем ось Z вдоль направления полей и примем, что в начальный момент частица находится в точке 0 и обладает скоростью, составляющей угол с осью Z. В перпендикулярной плоскости частица движется по окружности, радиус которой определяется выражением

(1.9)

Вдоль оси Z движение будет равномерно ускоренным (или замедленным) с ускорением

(1.10)

В результате траектория частицы будет представлять собой винтовую линию с переменным шагом.

Несколько более сложная картина возникает, если электрическое поле ориентировано под прямым углом к магнитному. Направим ось Y вдоль электрического поля, ось Z — вдоль магнитного поля и предположим для простоты, что начальная скорость частицы лежит в плоскости XY. В этом случае вся траектория частицы также будет лежать в этой плоскости. Уравнения движения имеют вид:

	(1.11)
	(1.12)

Введем вместо х новую переменную =х—ut, где и — некоторая постоянная. Физический смысл такого преобразования состоит в переходе к новой системе координат, которая движется относительно исходной со скоростью и в направлении оси X:

	(1.13)
	(1.14)

Если выбрать постоянную и равной Е/В, то уравнение (1.14) упрощается и система (1.13), (1.14) принимает вид:

	(1.15)
	(1.16)

Здесь и далее и определяется выражением (1.8).

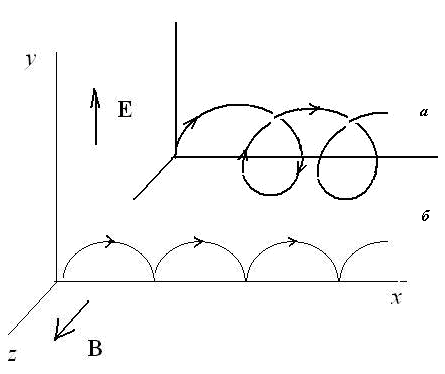
Электрическое поле исчезло из последних равенств, и они представляют собой уравнения движения частицы, находящейся под действием однородного магнитного поля. Таким образом, частица в новой системе координат (х, у) должна двигаться по окружности. Так как эта новая система координат сама перемещается относительно исходной со скоростью и=Е/В, то результирующее движение частицы будет складываться из равномерного движения по оси X и вращения по окружности в плоскости XY. Как известно, траектория, возникающая при сложении таких двух движений, в общем случае представляет собой трохоиду (рис. 1, а). В частности, если начальная скорость равна нулю, реализуется простейший случай движения такого рода - по циклоиде (рис. 1, б).

Рис. 1.1. Траектории движения заряженных частиц в скрещенных электрическом и магнитном полях: а) при ; б) при /

Другой интересный случай получается, если начальная скорость частицы направлена вдоль оси X и равна Е/В. При этом трохоидальная траектория вырождается в прямую линию, так как в системе координат (х, у) частица покоится.

Решение уравнений (1.15) и (1.16) с начальными условиями

(1.17)

имеет вид

(1.18)

Отметим, что движение заряженных частиц под действием скрещенных электрических и магнитных полей имеет общие черты с движением в неоднородном магнитном поле. В обоих случаях результирующее движение складывается из движения по окружности и поступательного переме­щения центра окружности — так называемого дрейфа. Следует, однако иметь в виду, что в отличие от дрейфа в неоднородном магнитном поле, где скорость дрейфа имеет противоположное направление для различно заряженных частиц, в скрещенных полях направление дрейфа не зависит от знака заряда.