5. Вычисление площади поверхности

Задачи с решениями

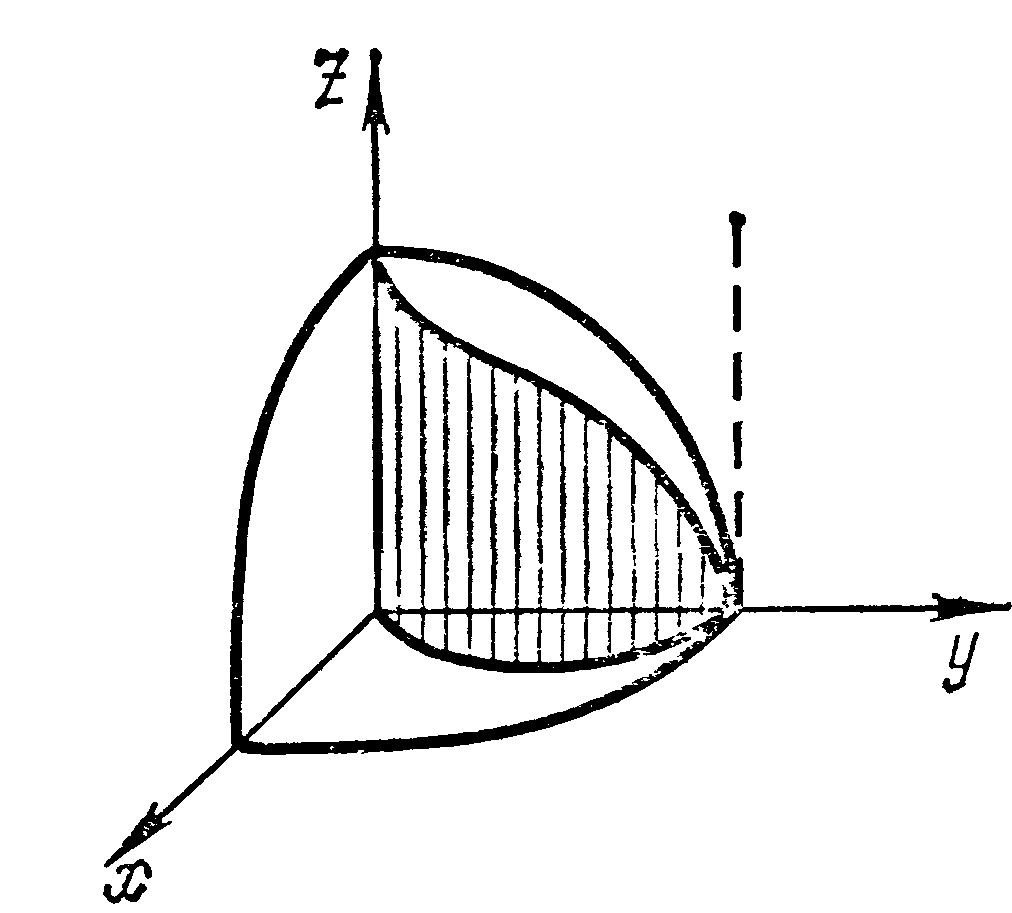
1. Найти площадь части сферы 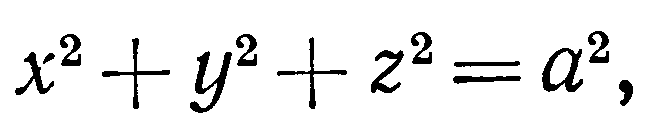заключенной внутри цилиндра

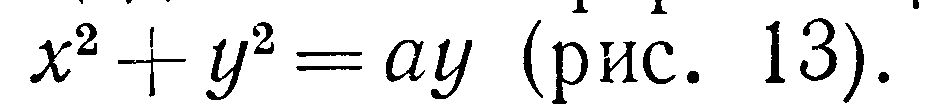
Решение Из уравнения сферы имеем (для I октанта):

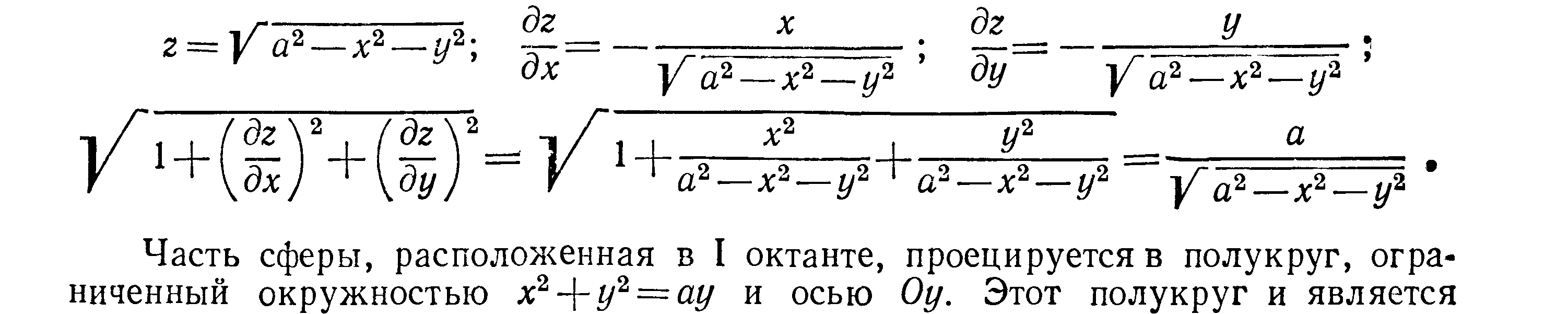областью интегрирования D. Поверхность расположена в четырех октантах потому искомая площадь

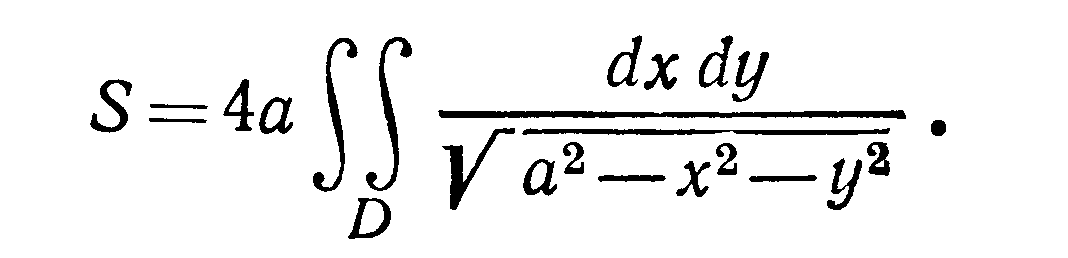
Перейдем к полярным координатам, тогда уравнение окружности примет вид

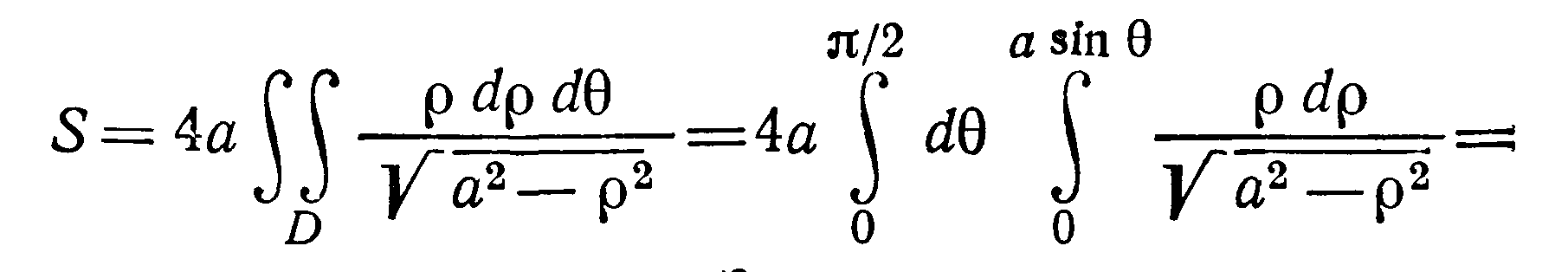
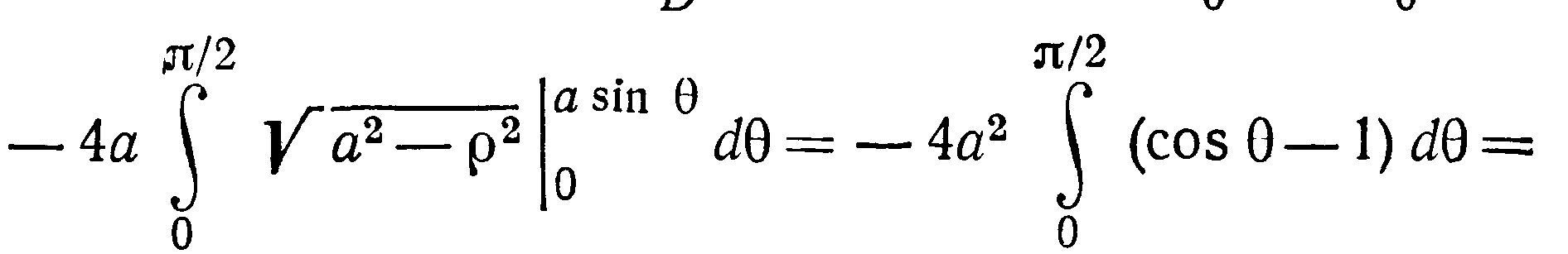
2. Найти площадь части конуса 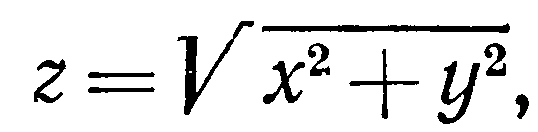внутри цилиндра

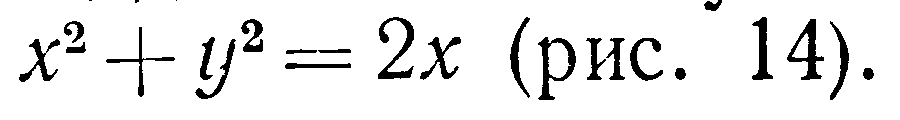
Решение Из уравнения конуса имеем Областью интегрирования D является круг, ограниченный окружностью

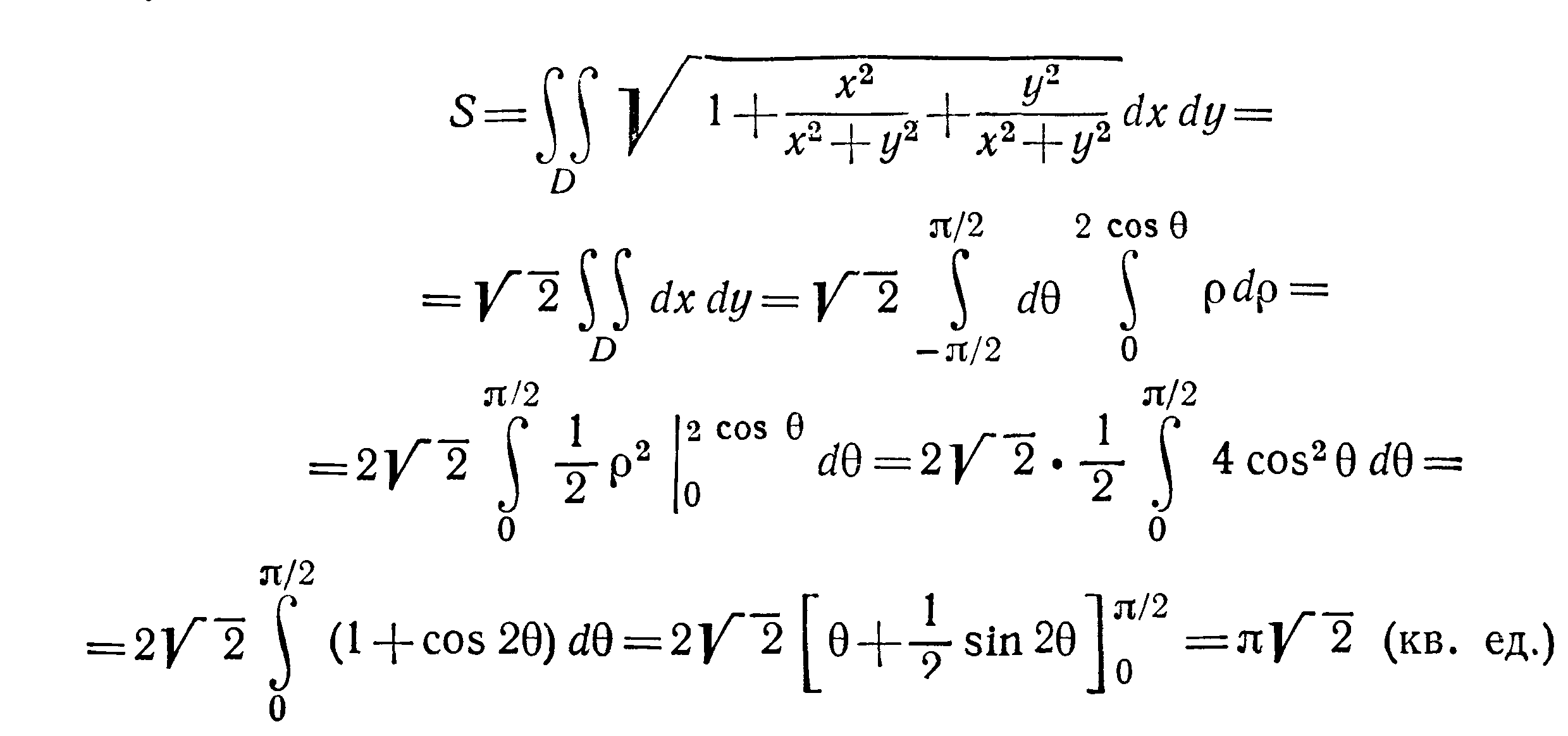
3. Вычислить площадь поверхности цилиндра 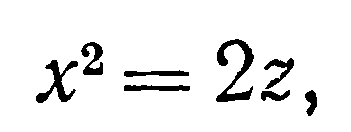отсеченной плоскостями

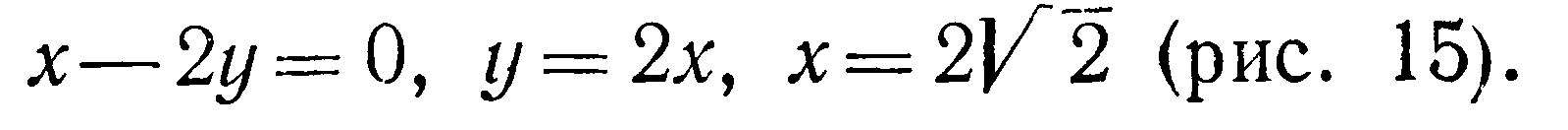
Решение Областью интегрирования служит треугольник ОАВ. Из уравнения цилиндра имеем

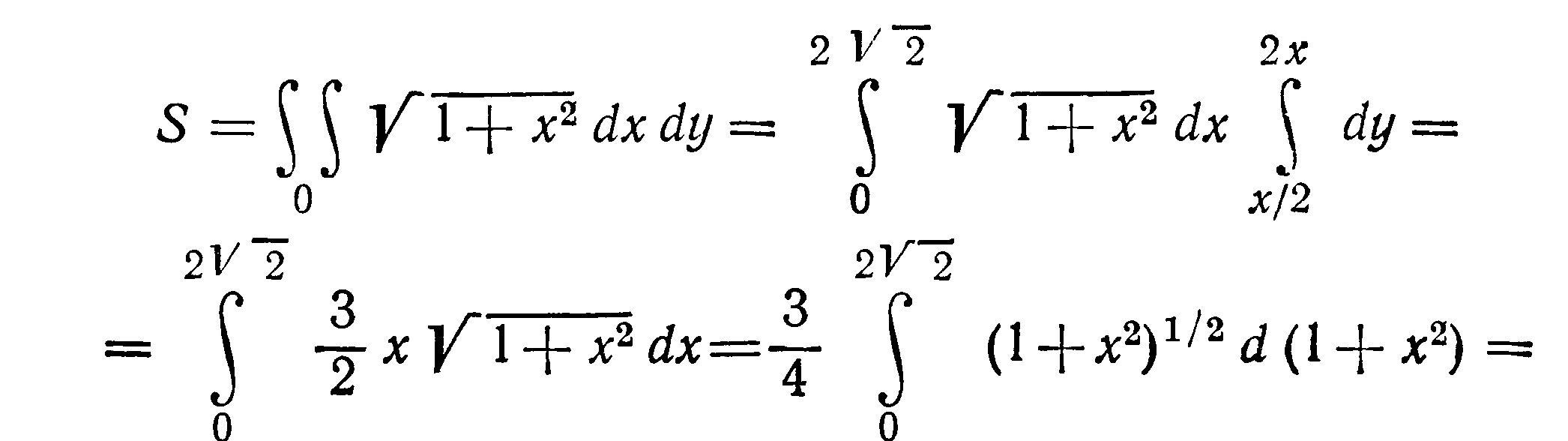
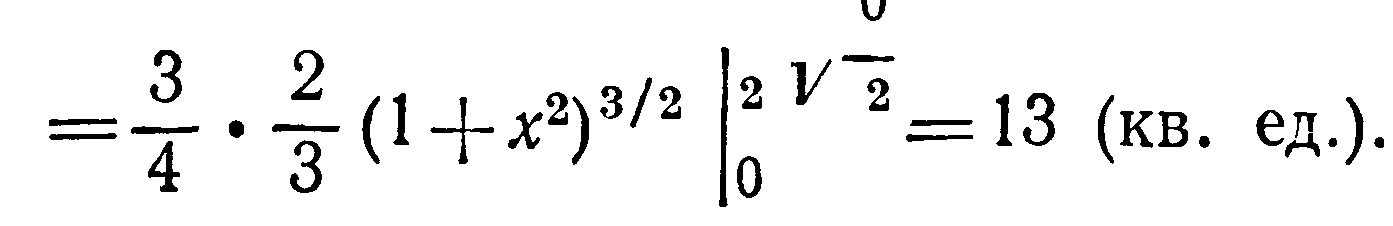
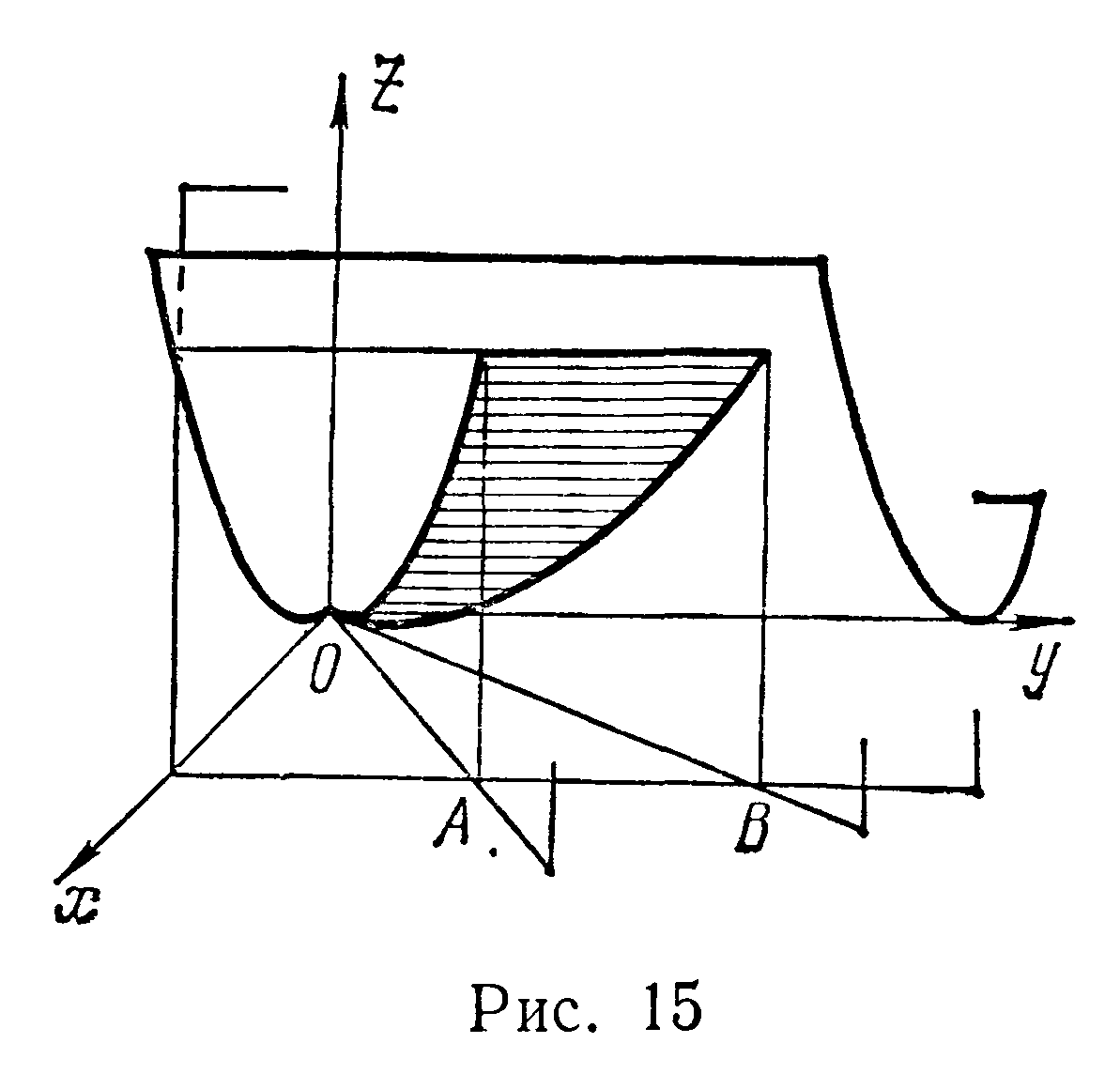
4. Вычислить площадь части поверхности параболоида x 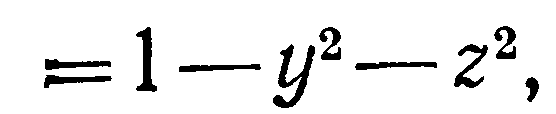, вырезанной цилиндром

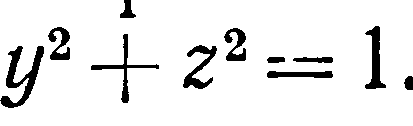
Решение Область интегрирования - окружность (она расположена в плоскости yOz). Из уравнения параболоида имеем

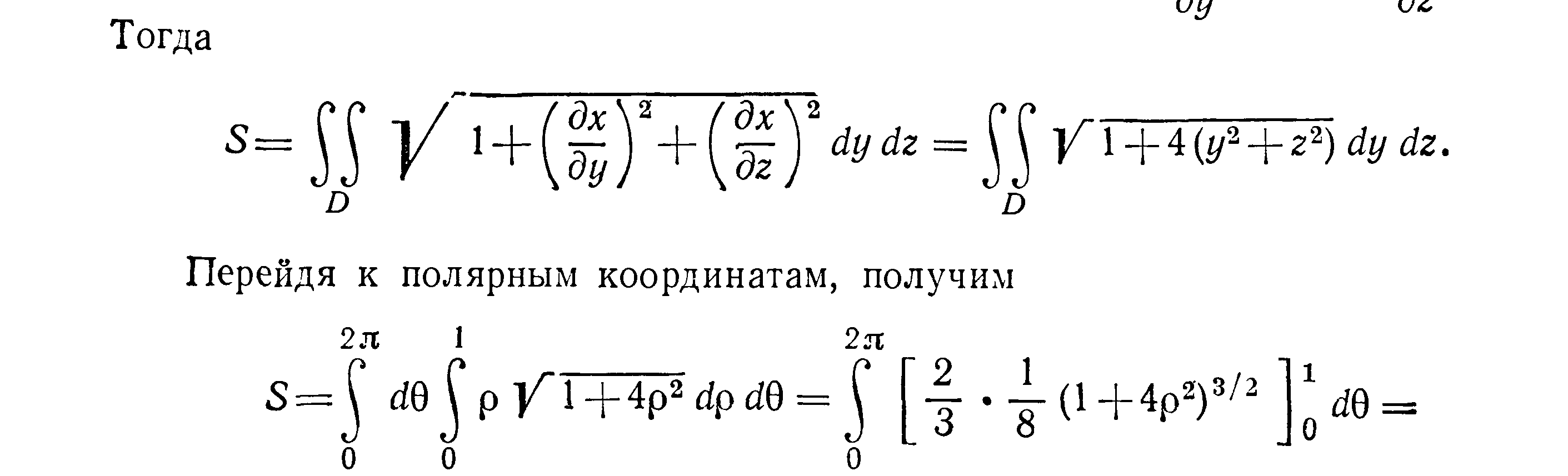
Задачи

36 . Найти площадь части поверхности вырезанной цилиндром

37. Найти площадь части сферы вырезанной цилиндром

38. Найти площадь той части плоскости z= x:, которая заключена внутри цилиндра

39. Найти площадь части поверхности цилиндра z = x², вырезанной плоскостями

40. Вычислить площадь поверхности конуса расположенной внутри цилиндра

41. Вычислить площадь поверхности цилиндра расположенной внутри цилиндра

42. Найти площадь части поверхности вырезанной плоскостями

Индивидуальные задания

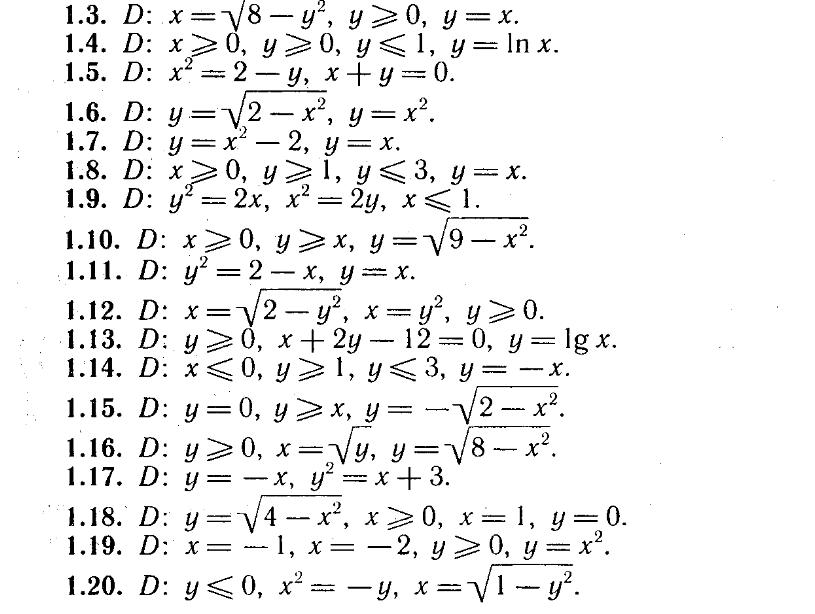
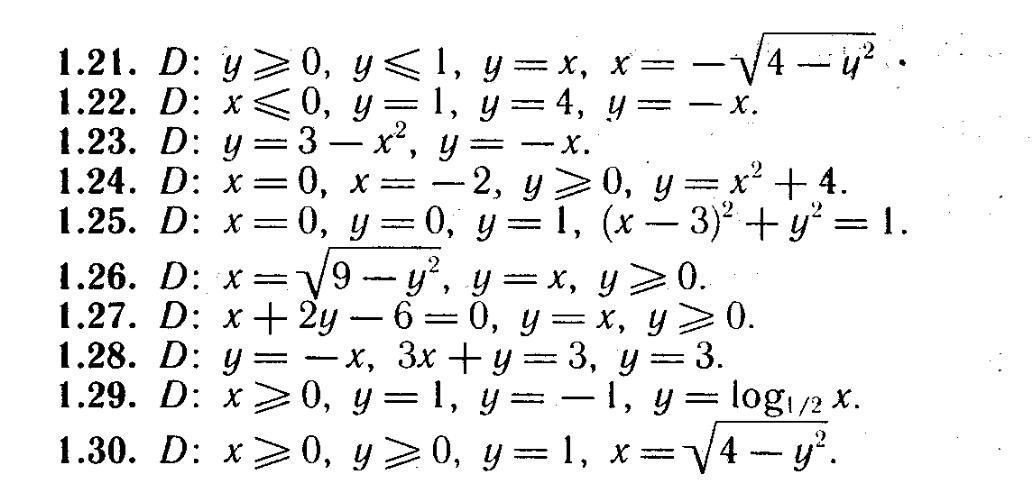
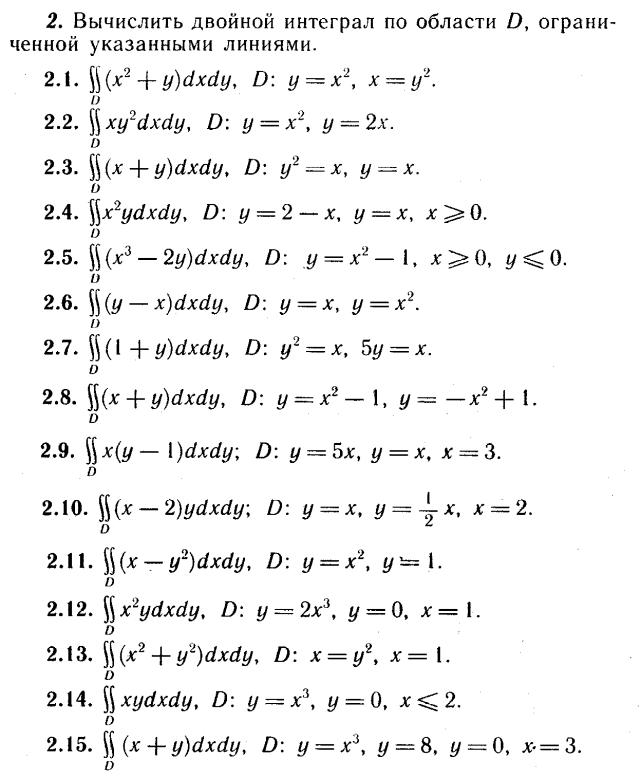
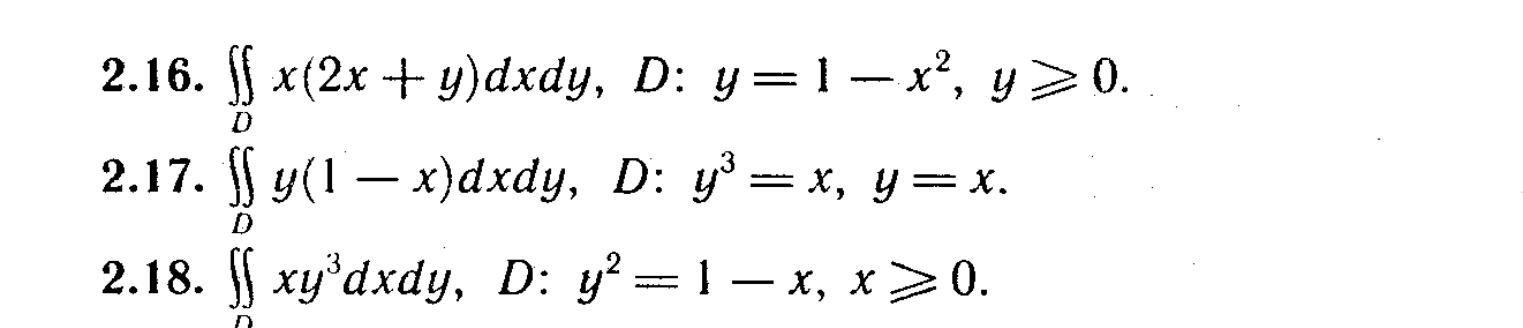
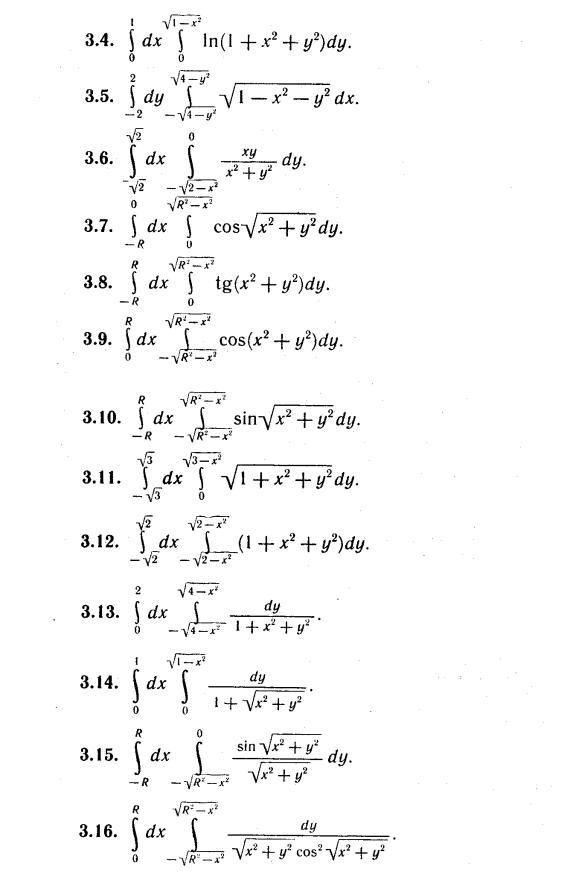
Тройной интеграл

Пусть функция f (х, у, z) определена в ограниченной замкнутой пространственной области Т. Разобьем область Т произвольным образом на п элементарных областей T₁ Т₂, ..., Т_n с диаметрами d₁ d₂, ..., dn и объемами ∆V₁, ∆V_{2, ….,}∆Vn. В каждой элементарной области возьмем произвольную точку P_k (ξ₁, ξ₂, … , ξ_n ) и умножим значение функции в точке Р_k на объем этой области.

Интегральной суммой для функции f (х, у, z) по области Т называется сумма вида

Предел интегральной суммы при стремлении к нулю наибольшего из диаметров всех элементарных областей ∆Vk называется тройным интегралом от функции f (х, у, z) по области Т и обозначается следующим образом:

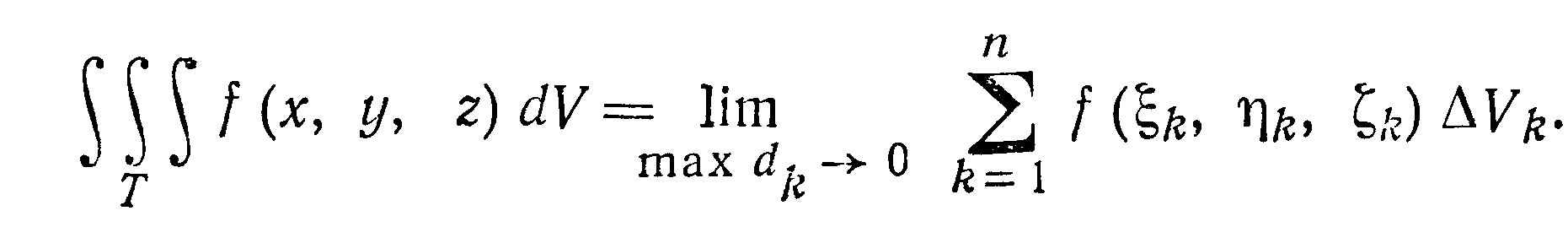
Конечный предел такого вида может существовать только для ограниченной

функции.

Если f (х, у, z) > 0 в области Т, то тройной интеграл

представляет собой массу тела, занимающего область Т и имеющего переменную плотность γ = f(x, у, z) (физическое истолкование тройного интеграла).

Основные свойства тройных интегралов аналогичны свойствам двойных интегралов.

В декартовых координатах тройной интеграл обычно записывают в виде

Пусть область интегрирования Т определяется неравенствами x₁≤ x≤ x_2, y₁≤ y ≤ y_2, z₁≤ z ≤ z_2, где y₁(x), y₂(x), z₁(x,y), z₂ (x,y) непрерывные функции. Тогда тройной интеграл от функции f (х, у, z), распространенный на область Т, вычисляется по формуле

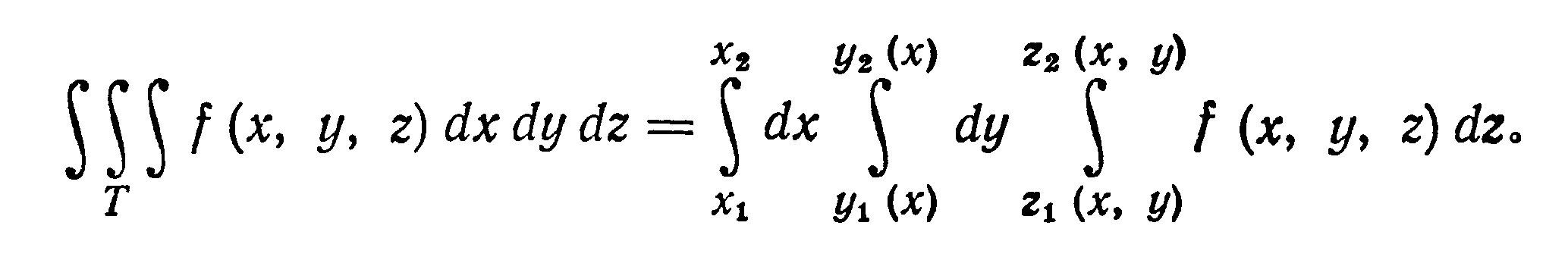
Если при вычислении тройного интеграла требуется перейти от переменных х, у, z к новым переменным и, v, w, связанным с х, у, z соотношениями х = х(u, v, w), y = y(u, v, w), z = z (u, v, w), где функции х(и, v, w), y(u,v, w) z (u, v, w), непрерывные вместе со своими частными производными первого порядка, устанавливают взаимно однозначное и в обе стороны непрерывное соответствие между точками области Т пространства Oxyz и точками некоторой области Т' пространства Ouvw и якобиан J в области Т’ не обращается в нуль

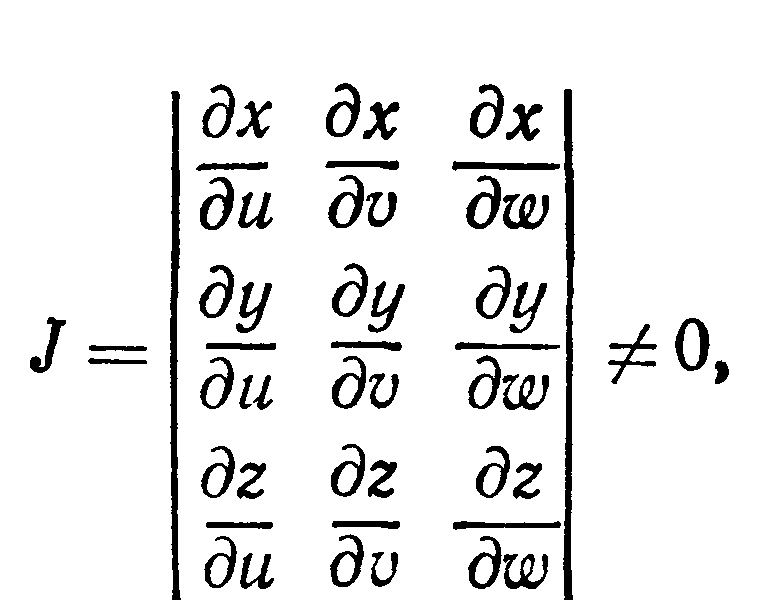
то пользуются формулой

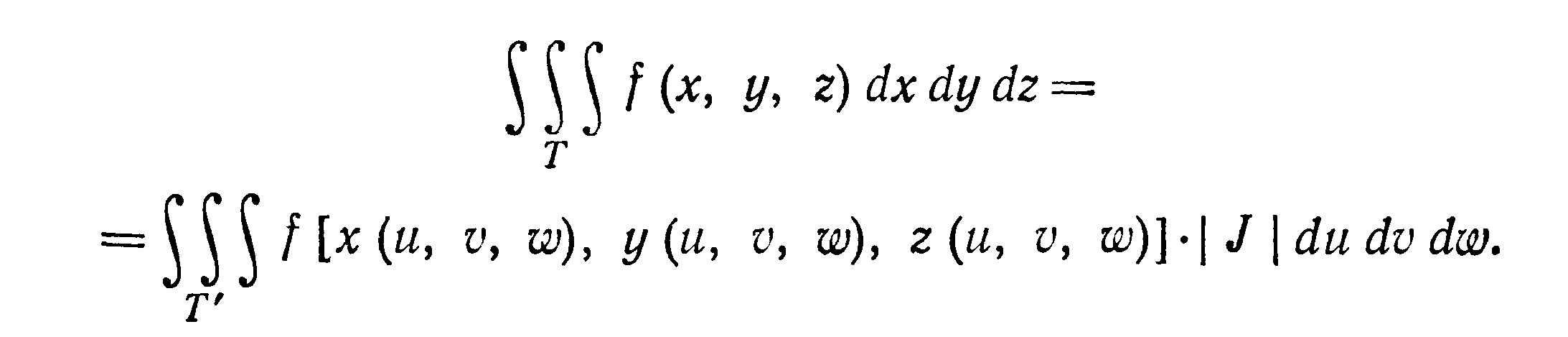
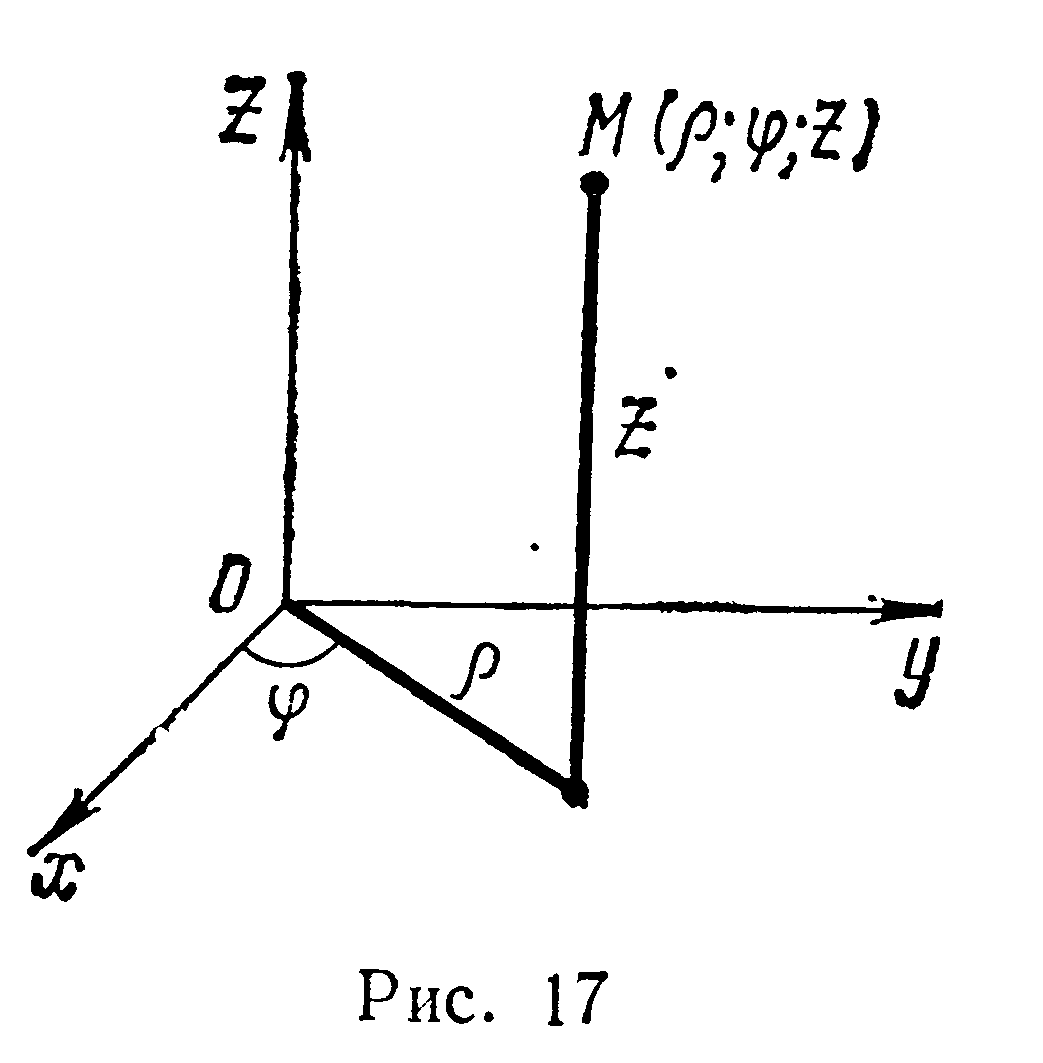
В частности, при переходе от декартовых координат х, у, z к цилиндрическим координатам ρ,φ , z (рис. 17), связанным с х, у, z соотношениями

якобиан преобразования J = ρ и формула преобразования тройного интеграла

к цилиндрическим координатам имеет вид

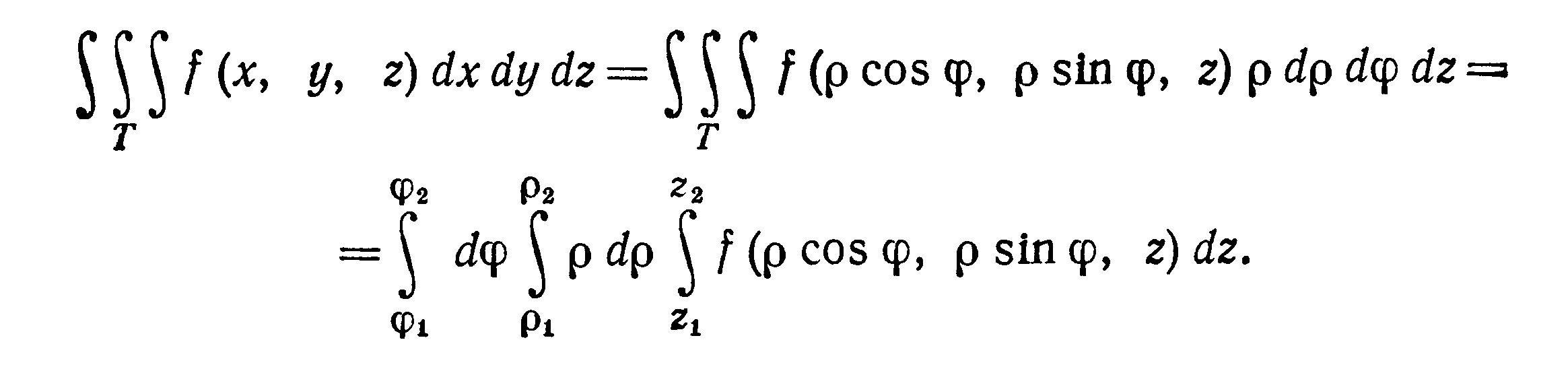
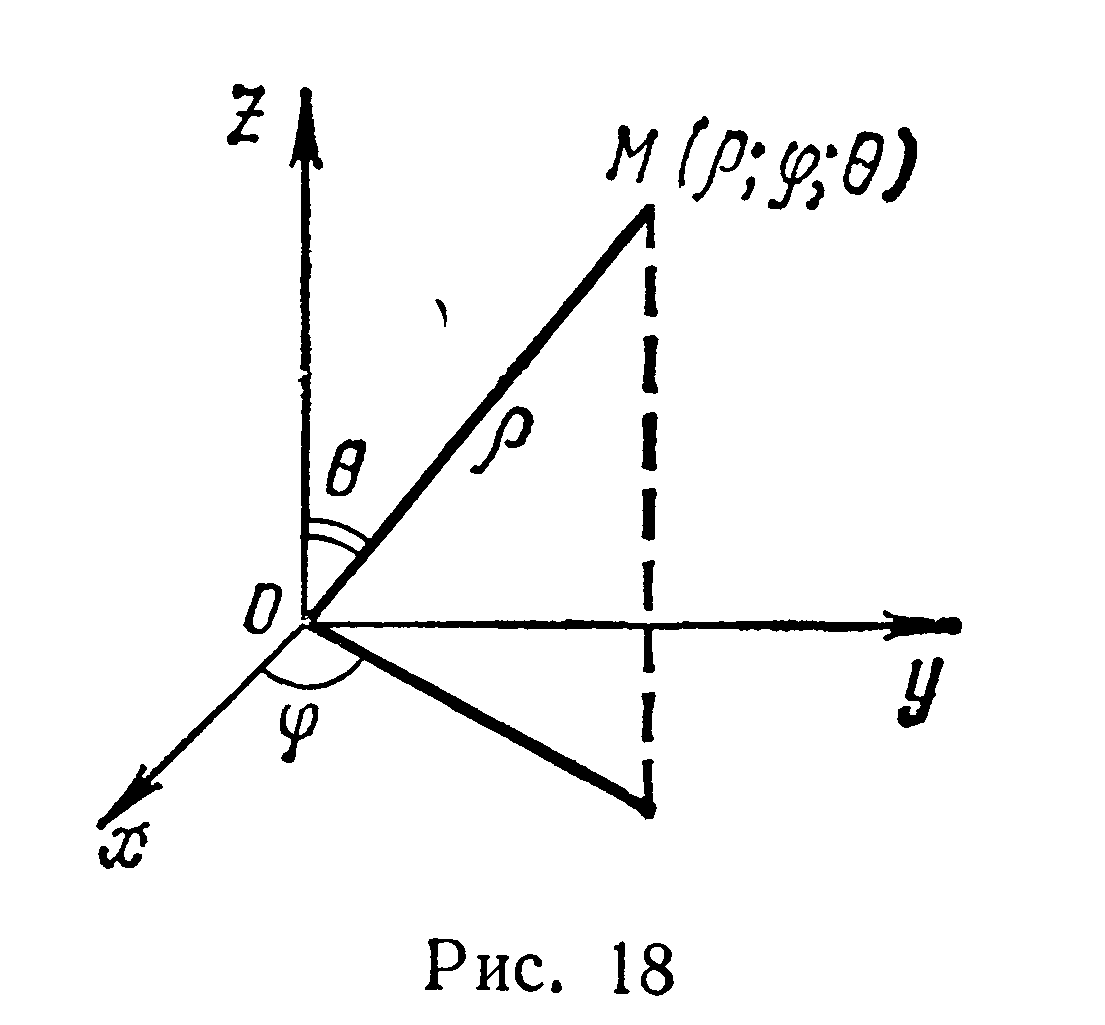
При переходе от декартовых координат х, у, z к сферическим координатам ρ,φ,θ (рис. 18), связанным с х, у, z соотношениями

якобиан преобразования J = ρ² sinθ, и формула преобразования тройного интеграла к сферическим координатам имеет вид