Empiryczny rozkład cechy

• Określenie empirycznego rozkładu cechy polega na przyporządkowaniu uszeregowanym rosnąco wartościom, przyjmowanym przez tę cechę, odpowiednio zdefiniowanych częstości ich występowania.

• Dane indywidualne - są to dane informujące, jaką wartość cechy ma każda jednostka badanej zbiorowości. Oznaczać je będziemy symbolem x_i, i = 1, 2,..., n. gdzie n jest liczebnością badanej zbiorowości.

Jeśli jest to cecha skokowa, to poszczególne wartości cechy mogą mieć taką samą wartość. Możliwe jest zatem pewne pogrupowanie obserwacji.

• Załóżmy więc, że cecha przyjmuje k wartości x_i, i = 1, 2,...,k (1<k<n). Przyjmijmy, że wartości te są uporządkowane tak, aby x_min= x₁< x₂<...., x_k= x_max, gdzie x_min oraz x_max oznaczają odpowiednio najmniejszą i największą wartość cechy.

• Liczbę jednostek, dla których cecha przyjmuje wartość x_i oznaczać będziemy symbolem n_i, przy czym .

• Niekiedy zamiast liczebności n_i, stosuje się częstotliwości jako: w_i= n_i/n, (i=1,...,k), oznaczające udział jednostek w ogólnej liczebności.

• Jeśli poszczególnym wartościom x_i cechy przyporządkowane zostaną liczebności n_i , to w ten sposób określony zostanie rozkład empiryczny, a uporządkowane odpowiednio obserwacje będą miały charakter danych pogrupowanych.

• Tablica prezentująca uporządkowane i pogrupowane dane nazywana jest potocznie szeregiem rozdzielczym.

• W przypadku cechy ciągłej określanie rozkładu odbywa się przez przyporządkowanie liczebności (częstości) odpowiednim przedziałom wartości cechy, a nie konkretnym jej wartościom. Takie przedziały nazywamy przedziałami klasowymi.

• Różnicę między górną i dolną granicą i-tego przedziału klasowego nazywa się rozpiętością przedziału (i oznacza się przez , gdy te wielkości są równe, lub przez h_i, gdy nie są równe).

• Przyjmuje się zwykle, że k, tj. liczba grup (klas), nie powinno być mniejsze niż 5 i większe od 20.

• Empiryczny rozkład cechy może być prezentowany za pomocą liczebności (częstości) skumulowanych. Taki sposób przedstawiania rozkładu empirycznego wiąże się z pojęciem dystrybuanty empirycznej i jest szczególnie użyteczny przy wyznaczaniu tzw. pozycyjnych charakterystyk rozkładu.

• Liczebność skumulowaną n(x_i) dla wartości cechy x_i oblicza się jako .

Przy budowie empirycznego rozkładu cechy ciągłej należy pamiętać o:

1. przedziałach klasowych [(x_di,,x_gi) , gdzie x_di oznacza dolną granicę przedziału, a x_gi – górną granicę przedziału i]

2. wielkości przedziału (Δ lub h_i – gdy są nierówne)

3. zamknięciu przedziału pierwszego (tj. wyznaczenie x_d1) oraz przedziału ostatniego (tj. wyznaczenie x_gk)

4. wyznaczeniu środka przedziału ( )

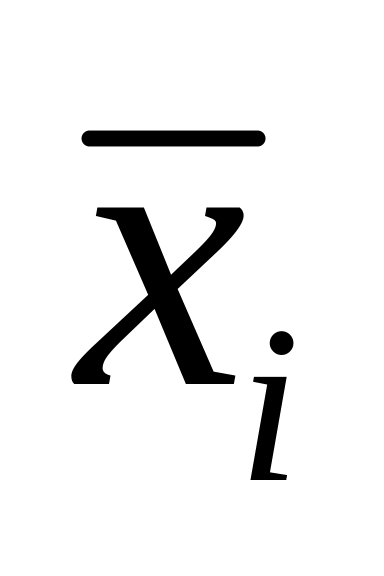5. liczebnościach (n_i) lub częstościach (w_i) przedziału

6. skumulowanych liczebnościach (n(x_i)) lub skumulowanych częstościach (w(x_i)) przedziału.

Tabl. Robocza. Rozkłady pracowników wg wysokości płacy miesięcznej

Nr grupy i	Grupy płacowe [xdi, xgi)	Średnia płaca w grupie i xi	Liczba pracowników ni	Częstości pracowników wi	Skumulowane częstości
1	400 -800	600	67	0,054	0,054
2	800-1200	1000	169	0,135	0,189
3	1200-1600	1400	286	0,229	0,418
4	1600-2000	1800	358	0,286	0,704
5	2000-2400	2200	175	0,140	0,844
6	2400-2800	2600	141	0,113	0,957
7	2800 -3200	3000	54	0,043	1,000
Ogółem	x	x	1250	1,000	x

Z powyższej tablicy obliczamy następujące parametry:

Przeciętną płacę:

Wariancję płacy:

Odchylenie standardowe płacy:

Współczynnik zmienności: , a w procentach 44,6%.

Frakcja elementów wyróżnionych, np. frakcja pracowników o płacy do 1600 zł:

, a w procentach 41,8%.

W dalszej części wykładu będziemy często prowadzili wnioskowanie odnośnie następujących parametrów z próby:

• przeciętnej ( - dla zmiennej ciągłej)

• frakcji elementów wyróżnionych (p - dla zmiennej dyskretnej)

• wariancji (s²)

• odchylenia standardowego (s)

• współczynnika zmienności (v)

W podanych podręcznika można znaleźć różne oznaczenia, dlatego należy przede wszystkim zorientować się co dane oznaczenie reprezentuje.