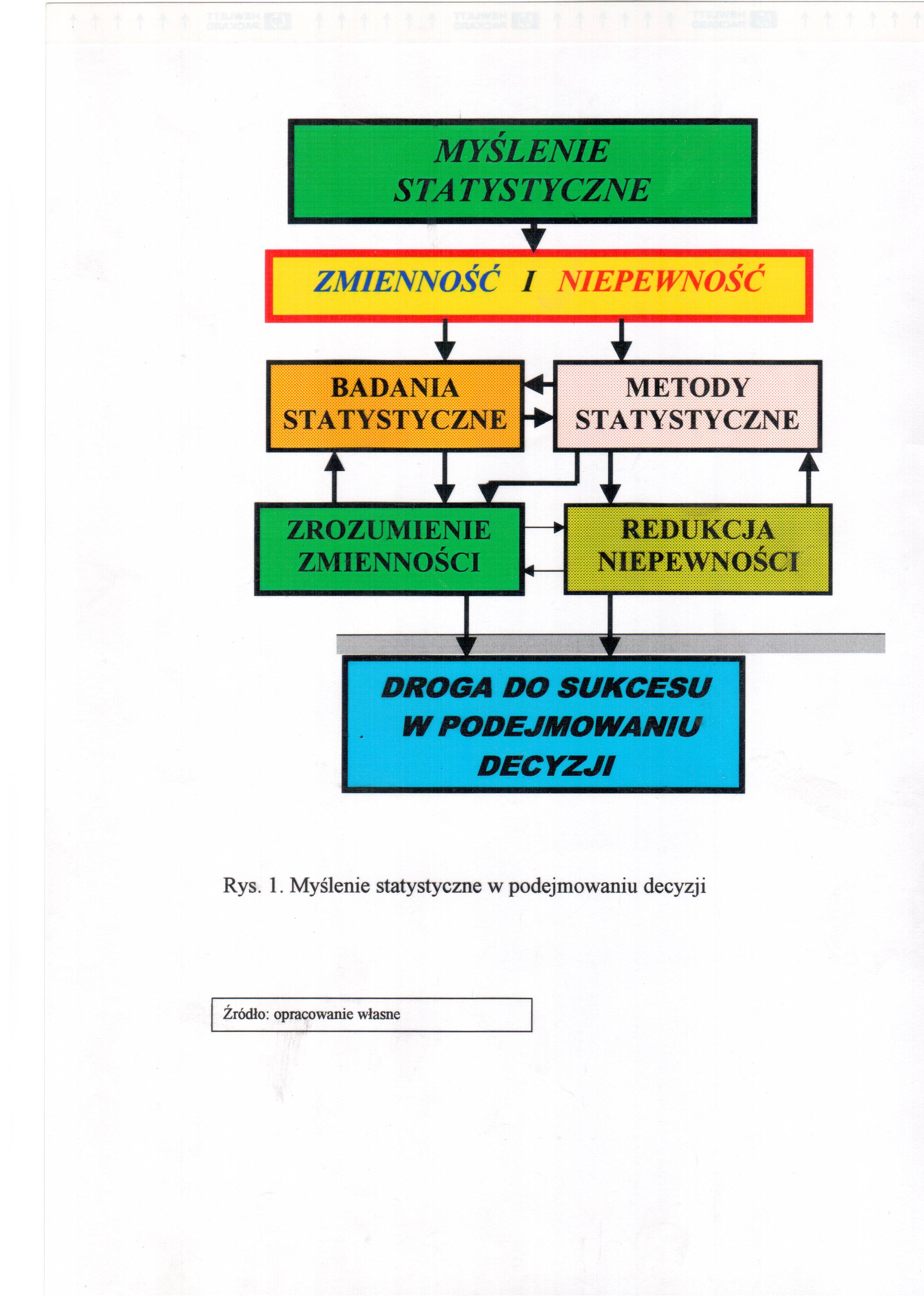
Myślenie statystyczne

Myślenie statystyczne jest filozofią uczenia się i działania opartego na trzech fundamentalnych zasadach:

• Każda działalność odbywa się w systemie procesów współzależnych

• Zmienność występuje we wszystkich procesach

• Zrozumienie i zredukowanie zmienności jest kluczem do sukcesu.

Definicja Mallowsa myślenia statystycznego:

“Myślenie statystyczne dotyczy relacji danych ilościowych do problemów świata rzeczywistego, w którym występuje zwykle zmienność i niepewność.”

Wynika stąd, że badania statystyczne oraz metody analiz statystycznych umożliwiają zrozumienie zmienności procesów i zjawisk masowych oraz zminimalizowanie niepewności, a to prowadzi do sukcesów w podejmowaniu decyzji. Graficznie przedstawiono te zależności na następnej stronie.

Podstawowe pojęcia w statystyce Zbiorowość (populacja) generalna

Podstawowym pojęciem w statystyce jest zbiorowość generalna zwaną także populacją generalną. Populacja generalna musi być zawsze w sposób jednoznaczny określona. Sprowadza się to do precyzyjnego określenia jednostek (elementów) wchodzących w skład badanej populacji. Przede wszystkim trzeba odpowiedzieć na trzy podstawowe pytania: co?, gdzie? i kiedy? (co należy badać, w jakich układach i przekrojach, w jakim okresie przeprowadzić badanie).

Jednostka (element)

Zbiorowość składa się z jednostek zwanych również elementami zbiorowości.

Liczebność zbiorowości (populacji)

Termin liczebność oznacza liczbę jednostek w populacji.

Mając określoną populację generalną, trzeba następnie odpowiedzieć na pytanie, jakie własności lub cechy będą nas w danym badaniu interesowały.

Cecha statystyczna

Elementy populacji generalnej mogą mieć różne właściwości pozwalające odróżnić jednostki zbiorowości, które podlegają obserwacji statystycznej. Właściwości te nazywamy cechami statystycznymi.

Cechy bywają mierzalne lub niemierzalne. Noszą one też nazwę cech ilościowych i cech jakościowych.

Cechy mierzalne I niemierzalne

Cechy mierzalne (lub ilościowe) - gdy jej odmiany wyrażone są liczbowo. Cechy te

mają charakter liczbowy (np. wiek, waga, wzrost, płaca, dochód).

Cechy niemierzalne (lub jakościowe) - gdy jej odmiany wyrażamy za pomocą określeń słownych. Mają charakter jakościowy (np. płeć, zawód, kolor oczu).

Cechy mierzalne ciągłe I skokowe

W statystyce rozróżnia się cechy mierzalne ciągłe i nieciągłe czyli skokowe.

Podział ten ma istotne znaczenie z punktu widzenia metod, jakie można stosować badaniu statystycznym.

Cechę nazwiemy ciągłą w pewnym przedziale, jeśli może ona przybrać wartość pośrednią pomiędzy każdą parą dowolnie dobranych wartości tego przedziału.

Zmienna ciągła przyjmuje więc nieskończenie wiele rożnych odmian, natomiast zmienna skokowa - tylko niektóre (przy czym w badaniach ekonomiczno-statystycznych spotyka się zwykle takie cechy skokowe, które przybierają tylko wartości całkowite, np. liczba osób w rodzinie).

Rozkład cechy

Elementy populacji generalnej różnią się na ogół między sobą wartościami rozpatrywanej cechy (lub cech) statystycznej; można więc mówić o rozkładzie cechy (cech) w populacji.

Ogólnie można powiedzieć, iż w celu uzyskania rozkładu populacji według badanej cechy, populacja ta powinna być w pewien sposób uporządkowana przy uwzględnieniu tej cechy. Przyjrzyjmy się tym zagadnieniom dokładnej oddzielnie dla cechy jakościowej i cechy ilościowe.