Алгоритм поиска наибольшего и наименьшего значений функции на ограниченном замкнутом множестве
1)
Построить множество
.
2)
Найти точки локального экстремума
функции
,
выбрать из них те, которые попадают
внутрь множества
,
и вычислить значение функции в этих
точках.
3) Последовательно
подставляя в функцию
уравнения линий
,
(или
),
ограничивающих множество, найти
наибольшие и наименьшие значения
получающихся функций одной переменной
(см. тему 12, п. 12.1) на границе
множества
и вычислить значения функции
в этих точках.
4) Из найденных значений функции выбрать наибольшее и наименьшее. Записать ответ.
Замечание. Множество может быть задано неравенствами.
Пример 2.
Найти наибольшее и наименьшее значения
функции
на множестве
Решение.
1) Множество
имеет вид прямоугольного треугольника,
ограниченного прямыми
,
,
(рис. 18.1).
2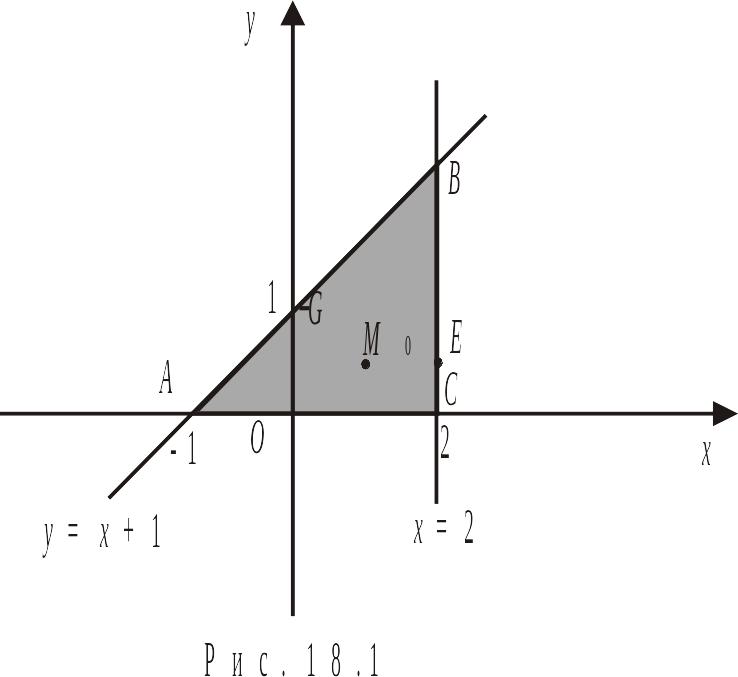
) Функция
имеет стационарные точки
и 
,
принадлежащей области
,
(см. пример 1), вычислим значение функции
в точке
:
.
3) Исследуем значения функции на границе множества .
Подставим
уравнение прямой
в функцию
и уравнение границы
.
Получится функция
,
.
Найдем ее наибольшее и наименьшее
значения на отрезке
:
,
тогда
.
Обозначим точку
.
Вычислим значение функции в этой
точке:
.
При
(точка
)
значение функции
.
При 
(точка
);
значение функции
.
Подставим
уравнение прямой
в функцию
и уравнение границы
.
Получится функция
,
.
Найдем ее наибольшее и наименьшее
значения на отрезке
:
,
тогда
,
то есть получилась точка
;
.
При
(точка
)
значение функции:
.
При
получается точка
,
.
Подставим
уравнение прямой
в функцию
,
тогда она примет вид
,
.
Найдем ее наибольшее и наименьшее
значения на отрезке
.
Уравнение
вещественных корней не имеет. Следовательно,
функция
на отрезке
не имеет стационарных точек. При
получается точка
,
.
При
получается точка
,
.
4)
Выпишем полученные значения функций:
,
,
,
,
,
.
Следовательно, наибольшего значения
функция достигает в точке
,
а наименьшего
в точках
и
.
Определение 6. Множество
пространства
называют выпуклым, если для
любых двух точек
и
,
принадлежащих
,
отрезок, соединяющий эти точки, также
целиком принадлежит множеству
.
Замечание. Выпуклыми множествами являются, например, вся координатная плоскость, полуплоскость, круг, выпуклый многоугольник.
Определение 7. Функцию
,
заданную на выпуклом множестве
,
называют выпуклой вниз, если
для любых двух точек
и
выполняется условие
.
Определение 8. Функцию
,
заданную на выпуклом множестве
,
называют выпуклой вверх, если
для любых двух точек
и
выполняется условие
.
Замечание. Выпуклой вниз функцией
является, например, функция
.
Для функции
выполняется как условие определения
7, так и определения 8, поэтому ее иногда
называют функцией нейтральной
выпуклости.
Теорема 3. Для того, чтобы функция
,
выпуклая и дифференцируемая на множестве
,
имела экстремум в точке
,
принадлежащей множеству
,
необходимо и достаточно, чтобы значения
ее частных производных в этой точке
были равны нулю:
.
Теорема 4. Экстремум выпуклой на множестве функции является глобальным, то есть наименьшим значением в случае функции, выпуклой вниз, и наибольшим значением в случае функции, выпуклой вверх.
18.3. Условный экстремум. Понятие о методе множителей Лагранжа
Рассмотрим задачу отыскания экстремума функции нескольких переменных на множестве, удовлетворяющем некоторому условию.
Пусть функция
определена и дифференцируема на своей
области определения. И пусть на ее
аргументы наложено условие
,
называемое уравнением связи.
Определение 9. Точку
называют точкой условного максимума
(минимума) функции
,
если существует такая окрестность этой
точки, что для всех точек
из этой окрестности, удовлетворяющих
условию
,
выполняется неравенство
(
).
Точки условного максимума и условного
минимума называют точками условного
экстремума.
Определение 10. Функцию
называют функцией Лагранжа, а
– множителем Лагранжа.
Теорема 5. Если точка
является точкой условного экстремума
функции
при условии
,
то существует значение
такое, что точка
является точкой безусловного экстремума
функции
.
Замечание 1. Если функции
и
заданы на выпуклом множестве и являются
выпуклыми (вверх или вниз), то для
нахождения условного экстремума функции
необходимо и достаточно найти стационарную
точку функции
.
Замечание 2. В точке условного экстремума линия уровня функции касается линии .
Алгоритм поиска условного экстремума функции
1) Найти область определения функций и , проверить, является ли их пересечение выпуклым множеством.
2) Проверить, являются ли функции и выпуклыми и какого характера (вверх ил вниз).
3) Составить функцию Лагранжа .
4) Найти стационарные точки функции Лагранжа. Возможны два случая:
а) в случае выпуклых функций и стационарная точка будет единственной; остается указать характер условного экстремума (максимум или минимум) на основании замечания 1 к теореме 5;
б) если не удалось установить характер выпуклости функций и , то стационарные точки функции Лагранжа являются только подозрительными на экстремум и требуют дополнительного исследования.
5) Вычислить значения функции в найденных точках. Записать ответ.
Пример 3. Найти точки условного
экстремума функции
при условии
.
Решение. Заметим, что уравнение
связи имеет вид
,
.
1) Функции
и
заданы на всей координатной плоскости
,
являющейся выпуклым множеством.
2) Проверим, является ли функция выпуклой, и установим характер выпуклости. Для любых двух точек и имеем:
,
то есть функция
является выпуклой вниз.
Проверим, является ли функция выпуклой, и установим характер выпуклости. Для любых двух точек и имеем:
,
то есть условие выпуклости вниз для функции выполняется.
3) Составим функцию Лагранжа:
.
4) Найдем стационарную точку функции Лагранжа как решение системы уравнений:
Таким образом, стационарная точка
функции Лагранжа
.
Следовательно, точка
является точкой условного экстремума
функции
при условии
.
В силу того, что функция
является выпуклой вниз, полученная
точка является точкой условного минимума.
5) Значение функции в точке
:
.
Ответ: точка является точкой условного минимума функции при , .
Замечание. Если число переменных больше двух, может рассматриваться несколько уравнений связи. В этом случае функция Лагранжа имеет вид
.