21.3. Математическая модель рынка с прогнозируемыми ценами
В теме 10 была рассмотрена простейшая
модель рыночного равновесия
,
когда функции спроса
и предложения
зависят только от текущей цены
на товар. В реальных ситуациях спрос и
предложение зависят также от тенденции
ценообразования и темпа изменения цены.
В моделях с непрерывной и дифференцируемой
зависимостью цены от времени эти
характеристики описываются, соответственно,
первой и второй производными функции
(
– время). В этом случае функции спроса
и предложения могут иметь вид
,
,
где
и
(
)
– вещественные числа. Записывая условие
рыночного равновесия
,
получим линейное неоднородное
дифференциальное уравнение второго
порядка с постоянными коэффициентами
относительно равновесной цены
.
(21.3)
Равновесную цену
,
определяемую дифференциальным уравнением
(21.3), называют неустановившейся,
так как значение
меняется с течением времени
.
Соответствующую модель рынка называют
нестационарной или динамической.
Если же значение цены
не зависит от времени
,
то равновесную цену называют установившейся.
Установившаяся равновесная цена
в динамической модели рынка определяется
условием
.
Замечание. Простейшая паутинная модель рыночного равновесия, рассмотренная в теме 10 (см. п. 10.5.1), является стационарной или статической моделью относительно установившейся равновесной цены.
По поведению неустановившейся равновесной
цены
по отношению к установившейся
равновесной цене
можно судить о состоянии рынка: стабильном
или неустойчивом. Для этого достаточно
вычислить
.
Если окажется, что
существует и равен нулю или не существует,
но 
– периодическая функция, то состояния
рынка стабильное. В этом случае
неустановившаяся равновесная цена
с течением времени достигнет установившейся
равновесной цены
.
Если окажется, что
бесконечен или не существует и
не является периодической функцией, то
дифференциальное уравнение (21.3) описывает
состояние паники на рынке. В этом случае
равновесная цена
с течением времени будет только удаляться
от установившейся равновесной цены
.
Пример 6. Функции
спроса и предложения имеют вид
,
.
Найти неустановившуюся и установившуюся
равновесные цены; выяснить, является
ли стабильным состояние рынка.
Решение. 1) Найдем неустановившуюся равновесную цену. Из уравнения рыночного равновесия получим линейное неоднородное дифференциальное уравнение, позволяющее найти неустановившуюся рыночную цену:
или
.
Выпишем соответствующее ему линейное
однородное дифференциальное уравнение
и характеристическое уравнение
.
Найдем корни характеристического
уравнения:
,
.
Так как они вещественны и различны, то
фундаментальная система решений
линейного однородного дифференциального
уравнения состоит из функций
,
,
а его общее решение имеет вид
.
Правая часть исходного линейного
неоднородного дифференциального
уравнения может быть представлена
следующим образом:
.
Так как
не является корнем характеристического
уравнения
,
то частное решение исходного линейного
неоднородного дифференциального
уравнения будем искать в виде
,
где
– некоторое, пока неизвестное, число.
Вычислим
,
подставим
и его производные в дифференциальное
уравнение
,
получим
или
.
Таким образом,
.
В силу теоремы 2 запишем общее решение
исходного линейного неоднородного
дифференциального уравнения
,
которое представляет собой неустановившуюся
рыночную цену.
2) Найдем установившуюся рыночную цену.
Для этого подставим
в дифференциальное уравнение
,
получим, что
или
– установившаяся рыночная цена.
3) Оценим состояние рынка. Для этого вычислим . Получим
.
Следовательно, состояние рынка стабильное.
З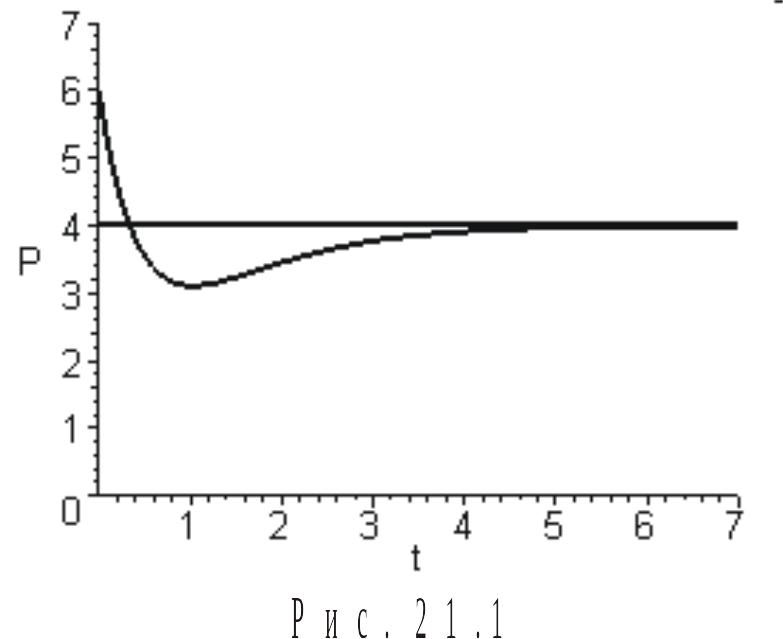
амечание.
Процесс приближения неустановившейся
равновесной цены к установившейся
показан на рис. 21.1. При построении функции
предполагалось, что в момент времени
даны начальное значение неустановившейся
равновесной цены
денежных единиц и начальное значение
ее первой производной (скорость цены)
денежных единиц в единицу времени.
Соответствующее частное решение имеет
вид
.
Теоретический материал: [1, гл. 12], [2, гл. 9], [3, гл. 9], [5], [8], [10], [12, гл. 19, 20], [17], [19], [21], [27], [33, ч. 2, гл. 4], [35, гл. 4].