11 Формулы в логических исчислениях. Формальная теория.

Правильно построенные высказывания называются препозиционными формулами.

Формулы имеют следующий синтаксис:

Формальная теория

1 Множество А символов, образует алфавит

2 Множество слов в алфавите А, называется формулами

3 Подмножество В формул, называется аксиомами

4 Множество отношений R на множестве формул, называется правилами вывода

12 Интеррпритация формул в логических исчислениях

Пусть А (х₁……, х_n) – пропозиционная формула, где х₁……, х_n – входящие в нее пропозиционные переменные

Конкретный набор истинностных значений, преписаных переменным, называется интерпретация формулы А.

Формула может быть истинной при одной интерпретации и ложной при другой

Формула, истинная при некоторой интерпретации, называется выполнимой.

Формула, истинная при всех возможных интерпретация, называется общезначимой.

Формула, ложная при всех возможных интерпретациях, называется невыполнимой.

14 Определение Графа

Графом G {V,E} называется совокупность двух множеств: непустого множества V(множества вершин) и множества E неупорядоченных пар различных элементов множества V (Е – множество ребер)

G(V,E) = (V,E) , V ,

Число вершин графа G обозначим p, а число ребер – а

13 История возникновения теории графов

Родоначальником теории графов считается Леонард Эйлер. В 1736 году в одном из своих писем он формулирует и предлагает решение задачи о семи кёнигсбергских мостах, ставшей впоследствии одной из классических задач теории графов.

Тео́рия гра́фов — раздел дискретной математики, изучающий свойства графов. В общем смысле граф представляется как множество вершин (узлов), соединённых рёбрами. В строгом определении графом называется такая пара множеств G={R,V}, где V есть подмножество любого счётного множества, а R — подмножество V×V.Теория графов находит применение, например, в геоинформационных системах (ГИС). Существующие или вновь проектируемые дома, сооружения, кварталы и т. п. рассматриваются как вершины, а соединяющие их дороги, инженерные сети, линии электропередач и т. п. — как рёбра. Применение различных вычислений, производимых на таком графе, позволяет, например, найти кратчайший объездной путь или ближайший продуктовый магазин, спланировать оптимальный маршрут.Теория графов содержит большое количество нерешённых проблем и пока недоказанных гипотез.

15 Смежность графа.

Матрица смежности – квадратная матрица является матрицей смежности графа , если при в графе вершины и соединены ребрами, при вершины и в несмежны.

Пример: для орграфа , изображенного на рисунке, приведем матрицу смежности:

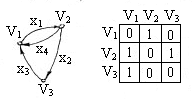
19,20,21 Комбинаторные конфигурации и задачи

Комбинаторика – раздел математики посвященный решению задач выбора и расположения элементов обычно конечного, множества в соответствии с заданными правилами.

1 Дано n предметов, их нужно разместить по m ящикам так, чтобы выполнялись заданные ограничения. Сколькими способами это можно сделать?

Рассмотрим множество функций

Не ограничивая общности можно считать что

Размещение

Назовём множество, содержащее n элементов, n-множеством.

Последовательность (x₁, x₂, …, x_k ) длины k без повторяющихся элементов из элементов данного n-множества назовём k-размещением. Обозначим символом А_n^k число размещений из n по k элементов (от фран. "arrangement" - размещение). Используя правило произведения, вычислим число А_n^k. Пусть произвольное размещение длины k имеет вид: (x₁, x₂, …, x_k ). Элемент x₁ можно выбрать n способами. После каждого выбора x₁ элемент x₂ можно выбрать (n - 1) способами. После каждого выбора элементов x₁ и x₂ элемент x₃ можно выбрать (n - 2) способами, и т.д. После каждого выбора элементов x₁ , x₂, …, x_k-1 элемент x_k можно выбрать (n - (k - 1)) = (n - k + 1) способами. Тогда, по правилу произведения, последовательность (x₁; x₂; , …, x_k ) можно выбрать числом способов, равным

n(n - 1)(n - 2) … (n - k + 1) = А_n^kПроизведение в левой части равенства умножим и разделим на (n - k)!, получим:  

А_n^k =  Если в формуле k = n, то А_nⁿ есть число P_n перестановок из n элементов P_n = n! (от "permutation"- перестановка).

Сочетания

k-подмножество данного n-множества называется k-сочетанием.Обозначим через число k-сочетаний из данных n элементов. Формулу для числа получим, рассуждая следующим образом. Если каждое сочетание упорядочить всеми возможными способами, то получим все k-последовательностей из n элементов, без повторений, то есть все k-размещения. Иными словами, Откуда:    или