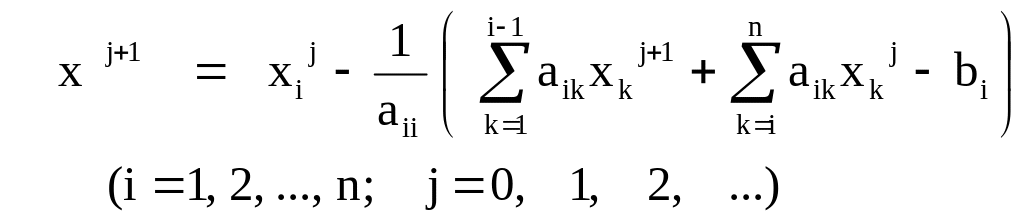О точности полученных приближений (x2, , xcp) можно судить по невязке:

F(x₂) = F(0,6070577) = - 0,0001569,

F( ) = F(0,6071207) = 0,0000681,

F(x_cp) = F(0,6071) = 0,000006.

5. Метод последовательных приближений (итераций)

Сущность метода. Для нахождения действительных корней уравнения F(x) = 0, где F(x) - непрерывная функция на [a; b], его заменяют равносильным уравнением

х = (х) (14)

Это можно сделать всегда, притом не одним способом. Например, уравнение

х³ - 9х + 3 = 0

можно представить так:

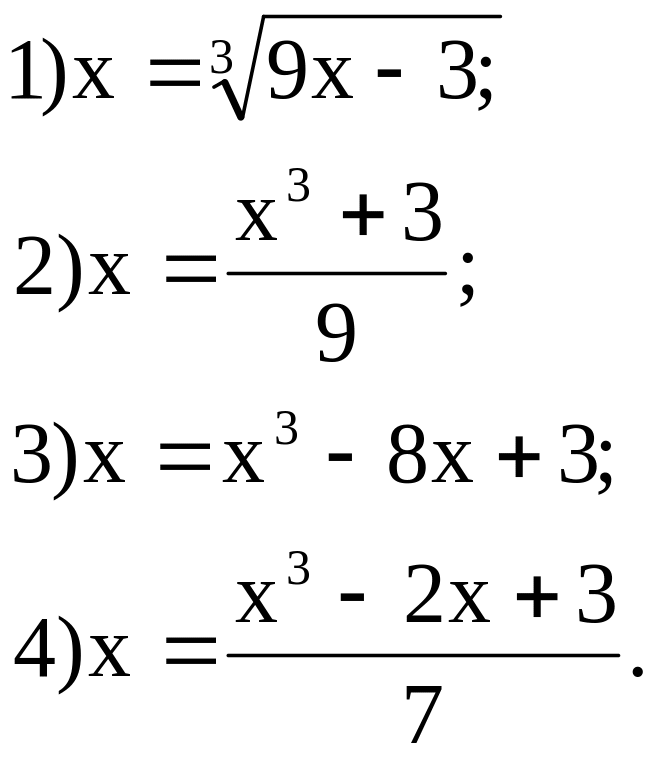
Пусть известен отрезок изоляции корня [a; b], тогда за начальное приближение искомого корня уравнения (14) берут: Подставляя значение х₀ в правую часть уравнения (14), получают первое приближение х₁ = (х₀). В качестве второго приближения берут х₂ = (х₁). Продолжая этот процесс дальше, получают числовую последовательность (х_n), определенную с помощью рекуррентной формулы:

x_n+1 = (x_n), (n = 0, 1, 2, ...) (15)

Полученная последовательность х₀, х₁, ..., x_n, x_n+1,... называется итерационной последовательностью, способ построения ее называется методом последовательных приближений или методом итераций численного решения уравнения.

При пользовании методом итераций необходимо выяснить основной вопрос: сходится ли полученная последовательность (х_n) к решению х^* уравнения (14) при возрастании n? Если последовательность (х_n) сходится, то есть существует предел х^* = то, переходя к пределу в равенстве (15) и, предполагая, что функция (х) непрерывна, получаем:

или x^* = (x^*). (16)

Следовательно, в этом случае х = х^* является корнем уравнения х = (х), а значит, и уравнения F(x) = 0.

Если же последовательность (х_n) окажется расходящейся, то есть не существует конечного предела построенной последовательности приближений (х_n), то это означает, что процесс итераций построен неудачно, и его надо заменить другим.

Следовательно, метод последовательных приближений применим при выполнении условия:

‘(x)  M₁ < 1 (18)

для всех х, принадлежащих отрезку изоляции корня уравнения (14), В этом случае процесс итераций сходится, и тем быстрее, чем меньше М₁; если же ‘(x) > 1, то итерационный процесс расходится. Для конкретной оценки величины m₁, определяющей скорость сходимости, проще всего пользоваться формулой: М₁ = max‘(x), где max берется по отрезку изоляции корня [а: b].

Точные и приближенные методы решения систем линейных уравнений

Самое простое уравнение — это линейное уравнение с од­ной переменной х вида:

ах = b. (1)

Обобщением таких уравнений является линейное уравнение с несколькими переменными х₁, х₂, ..., х_n вида:

a₁x₁ + a₂x₂ +...+ a_nx_n = b. (2)

Многие задачи сводятся к решению конечного множества уравнений вида (2), то есть системы линейных уравнений. В общем виде система n линейных уравнений с n переменными x₁, x₂,..., x_n записывается как совокупность числовых равенств:

(3)

Коэффициенты a_ij системы для их упорядочения снабжаются двумя индексами, причем индекс i соответствует номеру строки, а j —номеру столбца (i = 1, 2,..., n; j = 1, 2,..., n). Тогда свободный член запишется в виде b_i (i = 1, 2,..., n), а переменная— х_j (j = 1, 2,..., n). Будем далее считать, что упорядоченные наборы чисел a_ij, x_j и b_i берутся из множества действительных чисел R. Решением системы (3) n уравнений с n переменными называют упорядоченную совокупность n чисел c₁, c₂, ...,c_n . являющуюся решением каждого из уравнений, входящих в систему. Ясно, что эта совокупность чисел при подстановке ее в систему (3) вместо х₁, х₂, ..., х_n обращает каждое уравнение системы в истинное числовое равенство. Таким образом, множество решений системы является пересечением множеств решений, входящих в систему уравнений.

В частном случае, при n = 2 и n = 3 получаем хорошо знакомые системы двух линейных уравнений с двумя переменными:

(4)

и трех линейных уравнений с тремя переменными:

(5)

Решением системы (4) является упорядоченная пара чисел (c₁, c₂), а решением системы (5) — упорядоченная тройка чисел (с₁, c₂, c₃).

Известно, что исследование и нахождение решения для систем (4) и (5) не представляют особых трудностей. Но задачи практического содержания сводятся к исследованию и решению систем линейных уравнений, содержащих десятки, сотни и даже тысячи переменных. Число элементарных операций при решении линейных систем с n переменными пропорционально примерно n³, поэтому решение таких задач стало возможным только с появлением быстродействующих ЭВМ.

Не останавливаясь на вопросах исследования систем линейных уравнений, в дальнейшем будем предполагать, что система имеет единственное решение. Поэтому основной задачей этой главы и будет изучение универсальных вычислительных алгоритмов, используемых для нахождения единственного решения системы линейных уравнений, когда число переменных совпадает с числом уравнений.

Методы решения систем линейных уравнений можно разделить на две группы: точные и итерационные (приближенные) методы.

Точными являются такие методы, которые позволяют получить решение системы после выполнения конечного числа арифметических операций над коэффициентами системы и их свободными членами. Причем решение получится точным только тогда, когда коэффициенты и правые части системы (3) известны точно и все арифметические действия над ними выполняются без округлений. Из точных методов рассмотрим метод Гаусса и правило Крамера. Однако на практике даже этими методами не всегда удается получить точное решение, ибо в ЭВМ точные коэффициенты представляются приближенно с некоторой погрешностью, а в процессе вычислений необходимо проводить округление чисел.

Итерационными являются методы, позволяющие получать решение системы с заданной точностью путем сходящихся бесконечных процессов. Из приближенных методов рассмотрим ниже метод итераций.

1. Алгоритм метода Гаусса

Пусть дана система n линейных уравнений с n переменными:

Коэффициенты а_ij при переменных будем рассматривать как элементы двумерного массива A (N, N), а свободные члены b_i— как элементы одномерного массива В (N). Решение x_i(i = ) разместим в одномерном массиве В (N). Коэффициенты а_ij и свободные члены b_i будем рассматривать как элементы расширенной матрицы

.

Предписываемые методом Гаусса преобразования будем выполнять над элементами расширенной матрицы. Опишем формально алгоритм решения линейной системы методом Гаусса без выбора главного элемента.

1. Элементы первой строки расширенной матрицы (А | В) делим на а₁₁. Полученную после такого деления первую строку умножаем последовательно на a_k1(k = ) и вычитаем ее затем из k-ой строки (k = ). После этого преобразования в первом столбце массива A (кроме ) все элементы будут равны нулю, то есть получим матрицу:

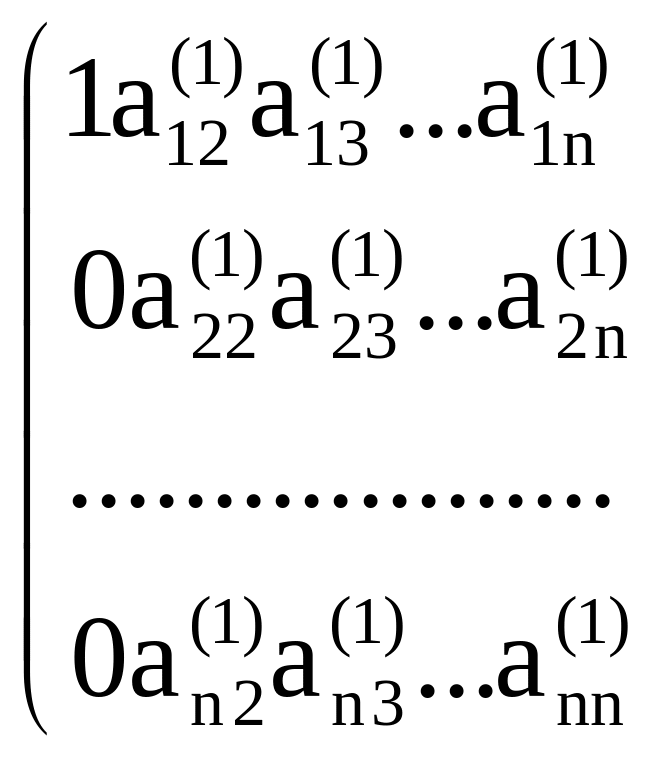
2. Элементы второй строки расширенной матрицы делим на , затем умножаем ее последовательно на и вычитаем из оставшихся строк при

3. Продолжаем этот процесс исключения переменных (получения нулей) до тех пор, пока подобная процедура не будет проделана с (n — 1)-й строкой матрицы. После этого получим матрицу:

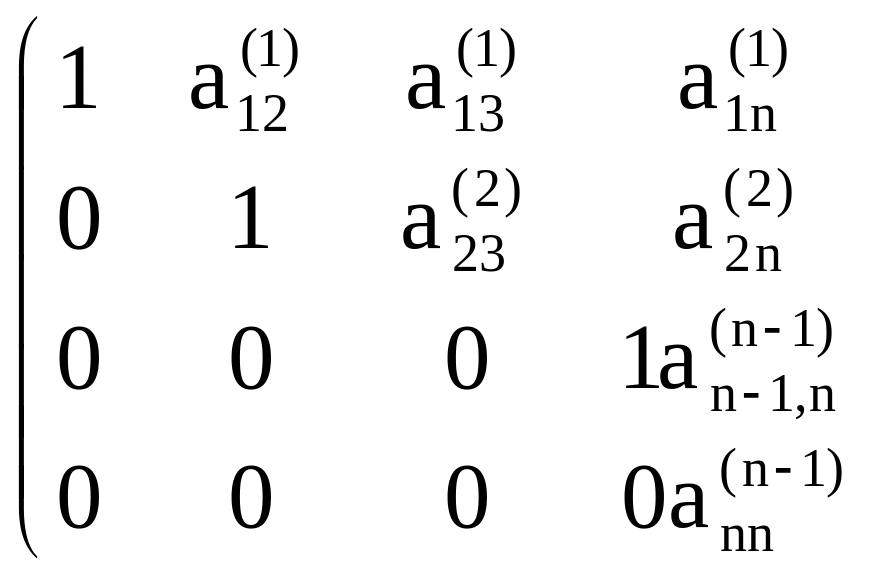
4. Элементы n-й строки делим на и в результате получаем:

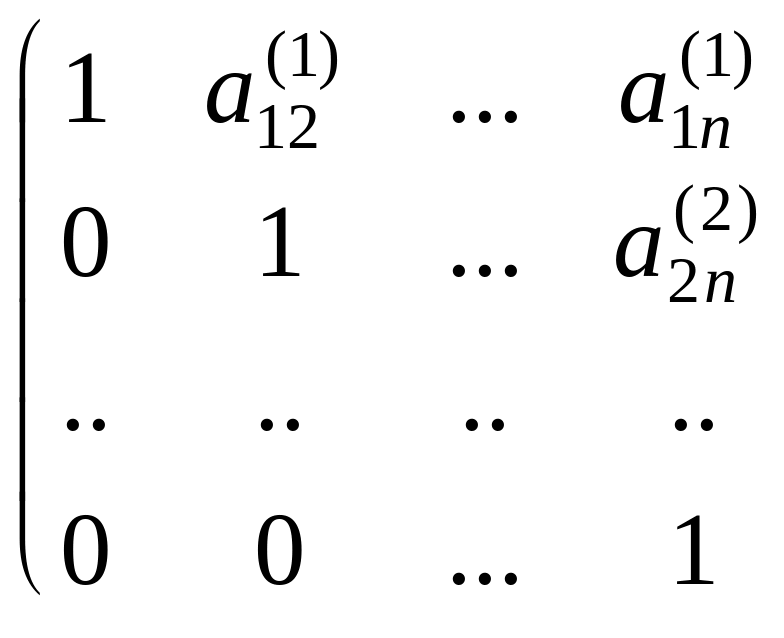
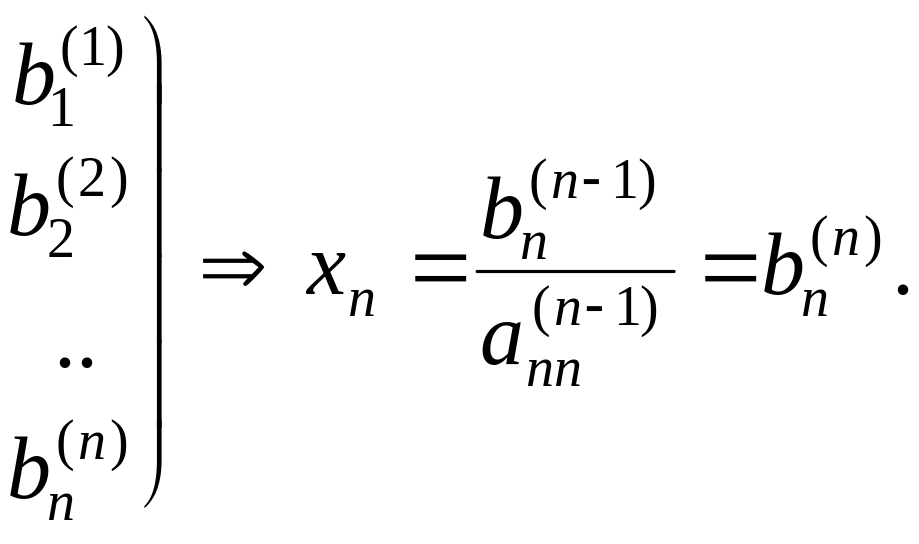
На этом закончился прямой ход метода Гаусса.

5. Выполняем обратный ход метода Гаусса: в (п—1)-ю строку последней матрицы подставляем значение х_n и находим значение x_n-1, затем последовательно находим x_n-2, x_n-3, ... , x₂, x₁ по формулам:

Этот алгоритм является экономичным в смысле использования памяти, так как все промежуточные и окончательные значения элементов в процессе преобразования матриц последовательно хранятся в тех же ячейках памяти, что и массивы А и В. Очередные значения диагональных элементов перед началом преобразования строк будем присваивать простой переменной D, что позволит хранить их до окончания преобразования очередной строки матрицы.

Значения переменных x_n, x_n-1, ...,x₁ присваиваются элементам массива свободных членов В.

Метод Гаусса с выбором главного элемента заключается в том, что при прямом ходе производится выбор наибольшего по модулю (главного) элемента и перестановка строк или столбцов. Последнее исключает деление на 0, если матрица коэффициентов содержит нулевые элементы, и повышает точность вычислений при наличии ошибок округления. Обычно для программ, ведущих вычисления с числами с плавающей точкой, достаточен выбор A_ii  0.

Метод вращения является разновидностью метода Гаусса. Он обладает повышенной устойчивостью к “провалам” промежуточных вычислений. Этот метод обеспечивает приведение исходной системы к системе с верхней треугольной матрицей (см. литературу).

2. Правило Крамера

Правило Крамера рассмотрим на примере двух линейных уравнений с двумя переменными:

(17)

хотя оно применимо и для решения системы n линейных уравнений с n переменными, но с увеличением n требует большого объема вычислительной работы.

Умножим первое уравнение системы (17) на коэффициент а₂₂, а второе — на — a₁₂ и полученные уравнения сложим. Тогда имеем:

Если a₁₁a₂₂ - a₂₁a₁₂ 0, то получаем значение переменной

Аналогично, умножая первое уравнение системы (17) на —a₂₁, второе — на а₁₁ и складывая их, получаем:

Введем обозначения: a₁₁a₂₂ - a₂₁a₁₂ = = ;

b₁a₂₂ - b₂a₁₂ =

a₁₁b₂ - a₂₁b₁ =

Следовательно, — определитель матрицы коэффициентов системы (17). Определитель получается из определителя , если коэффициенты системы (17) при x₁ (первый столбец матрицы А) заменить свободными членами

B = ;

Определитель — если заменить коэффициенты системы (17) при x₂ (второй столбец матрицы А) свободными членами.

Определитель называется главным определителем системы (17), а определители ₁ и ₂ — вспомогательными.

Если главный определитель , то матрица называется неособенной, в противном случае - особенной.

Таким образом, если главный определитель системы уравнений (17) , то система имеет единственное решение, определяемое формулами

(18)

Формулы (18) называются формулами Крамера.

Нахождение решения линейной системы (17) по формулам (18) называется правилом Крамера, который одним из первых пришел к понятию определителя и доказал сформулированное выше предложение.

Справедливы также следующие два предложения:

1. Если главный определитель системы (17) = 0, но хотя бы один из вспомогательных определителей ₁ или ₂ отличен от нуля, то система (17) не имеет решений (система несовместна).

2. Если все три определителя , ₁ и ₂ системы (17) равны нулю, но среди коэффициентов а_ij (i, j = 1,2) есть хотя бы один, отличный от нуля, то система (17) имеет бесконечное множество решений.

Легко дать геометрическое истолкование этим предложениям. Поскольку каждому уравнению системы (17) в плоскости соответствует некоторая прямая, то система (17) имеет единственное решение, если прямые имеют одну общую точку; не имеет решений, если прямые параллельны; и имеет бесконечное множество решений, если прямые сливаются.

Правило Крамера решения системы n линейных уравнений с n переменными имеет определенное теоретическое значение; практически им уже при n = 4 не пользуются. Установлено, что число операций умножения и деления, которые необходимо выполнить при решении линейной системы алгебраических уравнений порядка n по формулам Крамера, равно:

N(n) = (n² — 1)n! + n,

а по схеме единственного деления метода Гаусса:

N(n) = (n² + 3n — 1).

Для сравнения объема вычислительной работы по этим двум алгоритмам подсчитаем количество операций:

по Крамеру по Гауссу

при n = 5 2885 65

при n =10 360*10⁶ 430

Поэтому все современные ЭВМ имеют стандартные подпрограммы, реализующие различные модификации метода Гаусса.

3. Метод итераций и метод Зейделя

Метод итераций позволяет получить последовательность приближенных значений, сходящуюся к точному решению системы линейных уравнений. В отличие от метода Гаусса, метод итераций не требует контроля промежуточных вычислений, так как отдельные ошибки на каком-либо шаге итерации не искажают окончательных результатов, хотя и удлиняет процесс счета. Иначе говоря, метод итераций решения систем линейных уравнений является самоисправляющимся. Кроме того, метод итераций легко запрограммировать для ЭВМ. Пусть имеем систему

или, короче,

. (19)

Предположим, что определитель системы отличен от нуля и что диагональные коэффициенты

Выразим из первого уравнения x₁, из второго x₂, и т. д. Тогда получим эквивалентную систему:

где

Полученную систему запишем так:

(20)

и назовем ее системой нормального вида.

Будем решать ее методом последовательных приближений. За нулевое приближение возьмем, например, столбец свободных членов

Подставив в правую часть системы (20) значения (i = ), получим первое приближение: .

Затем аналогично второе: и т. д.

Таким образом, зная k-e приближение, (k + 1)-е приближение вычисляют по формуле (21)

Если последовательность приближений ( ) (j = ) имеет предел

то является точным решением системы нормального вида, а значит, и исходной системы. В самом деле, переходя к пределу при в (21), имеем:

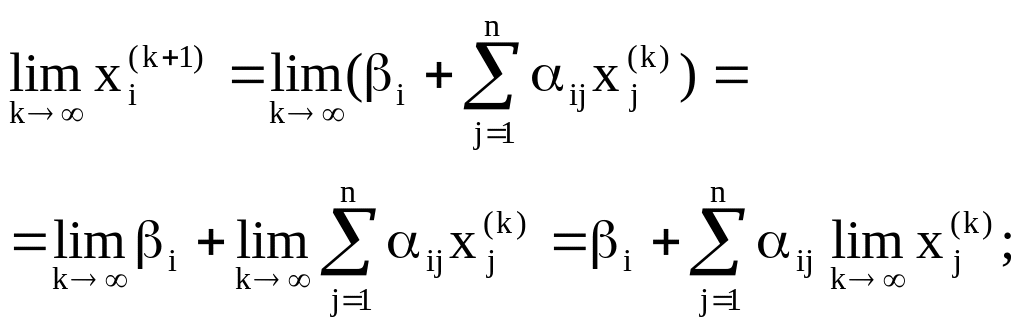
Описанный метод последовательных приближений называется методом итераций. Рабочие формулы метода итераций имеют вид:

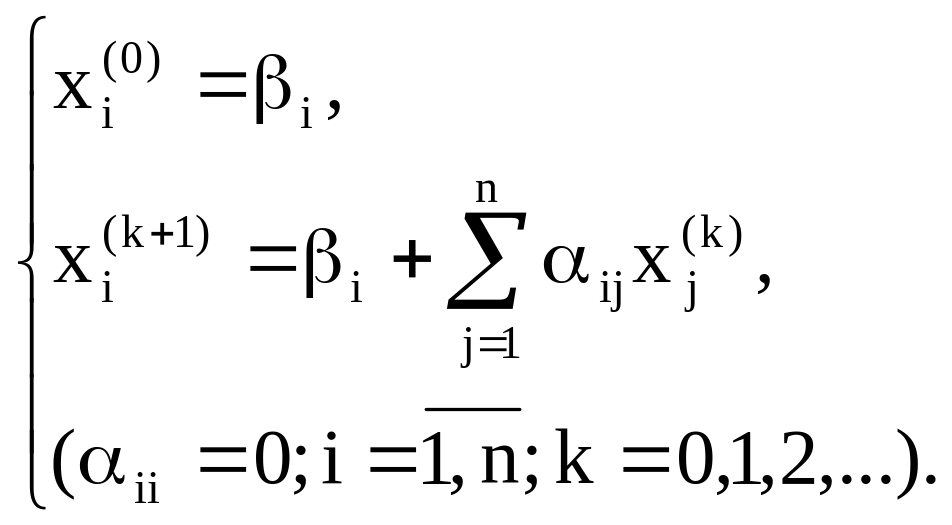(22)

Существование предела

гарантирует теорема о достаточном признаке сходимости процесса итераций.

Достаточным условием сходимости итерационных методов является условие

При методе Зейделя итерационный процесс подобен описанному для метода простых итераций, однако уточненные значения Х_i^j+1 сразу подставляются в последующие уравнения. Формула итерационного процесса имеет вид: