5. Алгоритм Берлекемпа розкладання многочлена на незвідні множники над скінченним полем

Нехай – нормований, вільний від квадратів многочлен степеня над полем 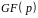. Для розкладання його на незвідні над полем множники застосовується алгоритм, запропонований Е. Берлекемпом (Elwyn R. Berlekamp) у 1967 р.

Алгоритм Берлекемпа ґрунтується на китайській теоремі про остачі для многочленів.

Теорема (китайська теорема про остачі для многочленів). Нехай в системі конгруенцій над полем

многочлени з попарно взаємно прості. Тоді існує єдиний многочлен такий, що і

, ,

де , ,

.

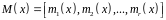Наслідок. Нехай в системі конгруенцій над полем

(6)

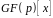многочлени з попарно взаємно прості. Тоді існує єдиний многочлен такий, що і

, ,

де , ,

.

Ідея алгоритму Берлекемпа полягає в тому, щоб скористатися наслідком з китайської теореми про остачі для многочленів наступним чином: якщо відомий многочлен , що задовольняє систему (6), то можна отримати розклад на множники за допомогою того факту, що якщо і , то 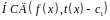ділиться на і не ділиться на .

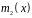Алгоритм Берлекемпа базується на наступних теоремах.

Теорема (про розклад многочлена на взаємно прості множники). Нехай 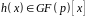, і

.

Тоді справедливий розклад многочлена на взаємно прості множники:

.

Якщо який-небудь многочлен буде побудований, то за його допомогою можна розкласти многочлен не менше, ніж на два множники. Метод побудови таких многочленів (які називаються 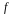-розкладаючими) дається наступною теоремою.

Визначимо матрицю порядку

, (7)

рядки якої є коефіцієнтами многочленів-лишків за модулем . Перший рядок цієї матриці завжди являє собою коефіцієнти многочлена , тобто , другий рядок являє собою коефіцієнти многочлена , третій – , останній – . Щоб знайти коефіцієнти цих многочленів, треба побудувати множину лишків за модулем для степенів , .

Теорема (про -розкладаючий многочлен) Многочлен буде задовольняти умові тоді і тільки тоді, коли вектор його коефіцієнтів 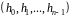є власним вектором матриці , що відповідає власному значенню 1.

Алгоритм Берлекемпа (Berlecamp’s Algorithm)

1. Побудувати матрицю (7).

2. Побудувати матрицю і знайти базис простору розв’язків системи лінійних алгебраїчних рівнянь . Нехай , , 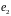…, – знайдений базис.

Зауваження. Оскільки перший рядок матриці (7) є , то перший стовпець матриці буде нульовим. Тому вектор завжди буде базисним.

3. Число знайдених базисних векторів дорівнює числу незвідних дільників многочлена в . При многочлен незвідний, вектору відповідає сталий многочлен . При треба взяти базисний вектор і побудувати -розкладаючий многочлен . За теоремою про розклад многочлена на взаємно прості множники, обчислюючи для всіх , знайти розклад на множники, де , .

Якщо , то алгоритм зупиняється. Якщо , то треба взяти базисний вектор , побудувати -розкладаючий многочлен , обчислюючи для вже знайдених множників , знайти подальший розклад , і т.д., доки не знайдемо всі множників.

Алгоритм зупиняється, коли знайдений розклад многочлена на множників, де .

Приклад 1. Розкласти многочлен 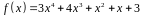на незвідні множники над за алгоритмом Берлекемпа.

Розв’язання. Замінимо даний многочлен на еквівалентний, старший коефіцієнт якого дорівнює 1. Для цього розв’яжемо конгруенцію

і найдемо . Тоді

і отримаємо еквівалентний нормований многочлен

.

1. Побудуємо матрицю . Перший рядок цієї матриці завжди являє собою коефіцієнти многочлена , тобто , другий рядок являє собою коефіцієнти многочлена , третій – , останній – .

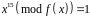Щоб знайти коефіцієнти цих многочленів, побудуємо множину лишків за модулем для степенів , . З рівняння виразимо або

.

Послідовно будемо підносити до степеня, замінюючи на .

,

,

Отримали другий рядок матриці – (3,0,4,2).

,

,

,

,

,

Отримали третій рядок матриці – (3,4,0,3).

,

,

,

,

,

Отримали четвертий, останній рядок матриці – (0,0,0,4).

Таким чином,

,

2. Побудуємо матрицю :

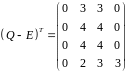
і знайдемо базис простору розв’язків системи лінійних алгебраїчних рівнянь . Розв’яжемо систему методом Гаусса:

.

Невідомі – базисні, – вільні. Виразимо базисні невідомі через вільні:

Останні рівності визначають загальний розв’язок системи:

, .

Надаючи вільним змінним спочатку значення , а потім , знайдемо базис простору розв’язків системи лінійних алгебраїчних рівнянь :

,

3. Число знайдених базисних векторів показує, що многочлен в має два незвідні дільника.

Вектору відповідає сталий многочлен .

Вектору відповідає многочлен .

Обчислимо для всіх .

При .

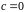
За алгоритмом Евкліда для многочленів знаходимо:

,

або після нормування

.

При .

За алгоритмом Евкліда для многочленів

,

або після нормування

.

Таким чином, маємо розклад многочлена на незвідні множники над :

.