§ 4. Закон Ампера. Взаимодействие параллельных токов

Действие магнитного поля на проводник с током было обнаружено в 1820 году Х.Эрстедом и А.Ампером (1775 – 1836). Французский физик Ампер подробно исследовал это явление и установил, что магнитное поле, действуя на какой-либо элемент тока (сила тока I, длина dl) приводит к появлению силы dF, которая пропорциональна элементу тока (Idl), магнитной индукции (В), а также синусу угла между направлением тока в проводнике и вектором (угол ):

(7)

Коэффициент пропорциональности в (7) зависит только от выбора единиц измерения. В СИ этот коэффициент выбирается равным единице:

dF = IdlBsin (8)

Было также экспериментально установлено, что направление силы, действующей на проводник с током в магнитном поле, оказывается перпендикулярным как направлению тока, так и направлению линий магнитной индукции (см. рис.6). Учитывая это обстоятельство, можно установить связь между векторами , и :

(9)

Выражение (9) описывает закон Ампера.

С

Рис. 6 Сила Ампера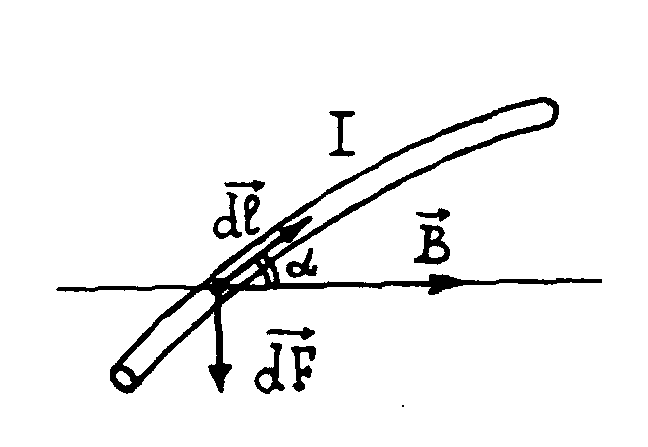

ила, действующая на провод с током конечной длины, находится из (9) путем интегрирования по всей длине провода:

(10)

Силы, действующие на токи в магнитных полях, называются амперовыми силами.

В международной системе единиц СИ закон Ампера играет основополагающую роль. Он используется для определения первичной единицы измерения электрических величин – 1 ампера.

1 Ампер – это сила такого постоянного тока, который проходя по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малого диаметра, расположенным на расстоянии 1 м один от другого в вакууме, вызывает взаимодействие этих проводников с силой 210^-7 Н на каждый метр длины проводника.

§ 5. Сила Лоренца. Движение заряженных частиц в магнитном поле

Как отмечалось выше, на проводник с током в магнитном поле в общем случае действует амперова сила. Магнитное поле действует на любой движущийся заряд. В проводнике без тока носители заряда двигаются хаотически, действующая на них со стороны магнитного поля сила все время меняет величину и направление, и поэтому результирующая сила оказывается равной нулю. В проводнике же с током упорядоченное движение носителей заряда приводит к появлению отличной от нуля результирующей силы.

Найдем выражение для силы, действующей на электрический заряд q, который движется в магнитном поле. По закону Ампера на элемент проводника dl с током I, находящийся в магнитном поле, действует сила, равная

(11)

где dN = nSdl – число носителей заряда в объеме проводника длиной dl.

Поделив обе части равенства (11) на число частиц dN, найдем силу , действующую на каждую заряженную частицу:

, (12)

где q, – заряд и скорость заряженной частицы, двигающейся в магнитном поле с магнитной индукцией .

Выражение (12) впервые было получено Х.Лоренцом. Поэтому сила, действующая на заряд q, движущийся в магнитном поле, называется силой Лоренца.

В общем случае, когда действуют и магнитное и электрическое поле (напряженностью ), на движущийся заряд действует сила:

, (13)

которая тоже называется силой Лоренца.

Сила Лоренца является важнейшим соотношением электродинамики, так как позволяет связать уравнения электромагнитного поля с уравнениями движения заряженных частиц.