Лебедев КММФЯ / Лебедев_4курс / Spetspraktikum_4_kurs

Специальный физический практикум

Задание 1

Электрон в одномерной бесконечно глубокой потенциальной яме

Электрон находится в одномерной бесконечно глубокой потенциальной яме

U(z) шириной a. Найти собственные волновые функции Ψ(z) и собственные значения энергии электрона. Построить огибающие волновых функций и квантованные уровни энергии в прямоугольной квантовой яме с бесконечно высокими стенками для различных значений ширины ямы (атомных монослоёв): а) 10 Å, б) 20 Å и в) 30 Å.

Задание 2

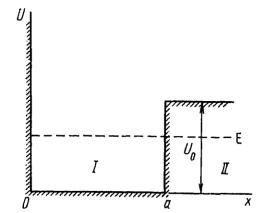
Электрон в одномерной полубесконечной потенциальной яме

Электрон находится в одномерной потенциальной яме U(z), имеющей бесконечно высокую стенку при z = 0 и конечную высоту U0 при z = a (рисунок).

Найти собственные волновые функции Ψn(z) и собственные значения энергии En (n

= 1, 2, 3, 4) электрона для связанных состояний системы (E < U0). Построить огибающие волновых функций и квантованные уровни энергии в квантовой яме для различных значений ширины ямы a и высоты барьера U0: а) 10 Å, 1 эВ, б) 20 Å, 5 эВ и в) 30 Å, 10 эВ.

0, 0 z a U z , z 0

U0 , z a

Задание 3

Электрон в одномерной потенциальной яме конечной глубины

Электрон находится в одномерной потенциальной яме U(z), имеющей конечную высоту U0 при z = ±a/2 (рисунок). Найти собственные волновые функции

Ψn(z) и собственные значения энергии En (n = 1, 2, 3, 4) электрона для связанных состояний системы (E < U0). Построить огибающие волновых функций для различных значений ширины ямы a и высоты барьера U0: а) 10 Å, 1 эВ, б) 20 Å, 5 эВ и в) 30 Å, 10 эВ.

Задание 4

Туннелирование электрона через потенциальную стенку

Электрон падает слева на потенциальную стенку, имеющую конечную высоту U0 при z = 0 (рисунок). Найти:

1) Собственные волновые функции Ψ(z) и собственные значения энергии E

электрона для состояний системы: а) E < U0, б) E > U0.

2)Найти коэффициенты прохождения D(E) и отражения R(E) электрона через

стенку.

3)Построить графики функций D(E) и R(E), а также огибающие волновых функций для заданного значения энергии и различных значений высоты барьера U0:

а) 1 эВ, б) 5 эВ и в) 10 эВ.

Задание 5

Туннелирование электрона через потенциальный барьер

Электрон падает слева на потенциальную барьер, имеющий конечную высоту U0 и ширину a (рисунок). Найти:

1) Собственные волновые функции Ψ(x) и собственные значения энергии E

электрона для состояний системы: а) E < U0, б) E > U0.

2)Найти коэффициенты прохождения D(E) и отражения R(E) электрона через

стенку.

3)Построить графики функций D(E) и R(E), а также огибающие волновых функций Ψ(x) для заданного значения энергии и различных значений ширины ямы

a и высоты барьера U0: а) 10 Å, 1 эВ, б) 20 Å, 5 эВ и в) 30 Å, 10 эВ.

0, x 0, a U x

U0 , x 0, a

Задание 6

Туннелирование электрона через двухбарьерную потенциальную стенку

Электрон падает слева на двухбарьерную потенциальную стенку, имеющую конечную высоту U0, ширину барьеров a и период b = 2a (рисунок). Найти:

1) Собственные волновые функции Ψ(z) и собственные значения энергии E

электрона для состояний системы: а) E < U0, б) E > U0.

2)Найти коэффициенты прохождения D(E) и отражения R(E) электрона через двухбарьерную стенку.

3)Построить графики функций D(E) и R(E), а также огибающие волновых функций Ψ(z) для заданного значения энергии и различных значений ширины ямы a

ивысоты барьера U0: а) 10 Å, 1 эВ, б) 20 Å, 5 эВ и в) 30 Å, 10 эВ.

0, z 0, a , b a, b 2a U z

U , z 0, a , b a, b 2a

0

Задание 7

Модель Кронига-Пени

Решить задачу о движении электрона в кристалле с периодическим потенциалом U(x) с периодом с = a + b. Найти разрешенные значения энергии электрона для связанных состояний в кристалле (E < U0).

0, nc x nc a

U x U0 , nc a x n 1 c