Лебедев КММФЯ / Лебедев_4курс / 1_Infinity_pits

Нестационарное уравнение Шрёдингера ¶

Но если квантовая механика — это не физика в обычном смысле, если она не занимается ни веществом, ни энергией, ни волнами, ни частицами, то чем же она занимается? С моей точки зрения, она занимается информацией, вероятностями, наблюдаемыми величинами и тем, как они соотносятся друг с другом.

Скотт Ааронсон

Это временное уравнение Шрёдингера, и оно описывает эволюцию волновой функции для изолированной квантовой системы во времени. т.е. если дать начальное условие , и проинтегрировать данное уравнение, то мы получим ответ на то, что станет (или что было) с волновой функцией в момент времени t. Уравнение Шрёдингера не выводится, а постулируется методом аналогии с классической оптикой, на основе обобщения экспериментальных данных.

Сматематической точки зрения — это дифференциальное уравнение в частных производных. Уравнение в частных производных имеет множество решений. В каждой конкретной задаче из этого множества следует выбрать одно решение, отвечающее условиям задачи.

Сфизической точки зрения нужно отметить, что согласно уравнению Шредингера волновая функция изменяется детерминировано, то есть совершенно однозначно. В этом смысле квантовая механика напоминает классическую, в которой движение системы заранее предопределено начальными условиями. Однако сама волновая функция имеет вероятностный смысл. Можно сказать, в квантовой механике детерминировано изменяются вероятности, а не сами физические события. События же всегда случайны и совершаются непредсказуемо.

Наконец, необходимо отметить еще одну очень важную особенность уравнения Шредингера: оно линейно. Волновая функция и ее производные входят в него в первой степени и для волновых функций справедлив принцип суперпозиции. Он в квантовой механике играет очень важную роль, так как позволяет сложные движения раскладывать на более простые подзадачи. Например, движение свободной частицы выражается отнюдь не только волнами де-Бройля. Возможны более сложные выражения для результирующих волновых функций той же свободной частицы. Вместе с тем согласно принципу суперпозиции любое сложное движение свободной частицы можно представить как сумму волн де-Бройля.

Уравнение Шредингера является математическим выражением корпускулярно-волнового дуализма микрочастиц. В предельном случае, когда длины волн де Бройля значительно меньше размеров рассматриваемого движения, уравнение Шредингера позволяет описывать движение частиц по законам классической механики.

В то же время одномерное уравнение Шредингера – это волновое уравнение, по структуре подобное уравнению колебания струны. Однако, решения уравнения Шредингера прямого физического смысла не имеют.

координате :

Используем метод Фурье. Итак, поскольку в нашем уравнении операторы действуют на абсолютно разные переменные, предположим, что мы можем

левую и правую части на саму волновую функцию (да, она может быть и нулём, идите нафиг):

в котором левая часть зависит только от t, а правая только от x. Так вот, когда же две функции зависящие от разных переменных могут быть равны друг другу? Правильно, если только они от этих переменных не зависят, т.е. они – константы. Обозначим эту константу как E, как некоторую энергию, чисто из размерности

следовательно получаемый спектр оператора H обладает всеми ништяками спектра оператора. Энергия – одна из наблюдаемых, следовательно, это уравнение на допустимые наблюдаемые значения энергии и на соответствующие им состояния системы . Данное уравнение и называется стационарным уравнением Шрёдингера, и оно даёт все возможные состояния консервативной системы, которая бесконечно долго покоится, пока её не трогают.

времени, а второе – только от координат , а зависимость её от времени и так известна. Именно из-за стационарного уравнения Шрёдингера квантовая механика является квантовой. Дело в том, что для многих физически важных систем оказывается, что спектр гамильтониана H оказывается дискретным (ну или имеет дискретную часть).

Иными словами, существуют решения, между которыми спектр меняется рывками, т.е. энергия при переходе от одного состояния к другому меняется не непрерывно, как в классмехе. Подобные состояния в классической механике соответствуют траекториям, ограниченным в пространстве, т.е. неразбегающимся частицам – связанным состояниям (когда частицы привязаны друг к другу некой силой – потенциалом). То, что возможны не любые состояния, а только избранные и называют квантованием (или дискретизацией). Непрерывный же спектр, который не вписывается в , соответствует траекториям, где частицы убегают друг от друга бесконечно далеко (т.е. случаю рассеяния). В этом случае тоже возможны эффекты, не наблюдаемые в классической механике (например, резонансные состояния), но квантования тут уже, естественно, нету.

Электрон в одномерной бесконечно глубокой потенциальной яме

Получили дифференциальное уравнение для гармонического осциллятора. Вспомним, как решаются линейные ОДУ:

и в нашем случае:

Это решение стационарного УШ. - это просто удобное обозначение констант, потом пригодится. Перейдем к яме с бесконечными стенками:

In [1]: using Luxor cd("C:\\Users\\User\\Desktop\\Mycop")

In [30]: @png begin fontsize(18) l=200

X, U, zer = Point(0.5l, 0.5l), Point(-0.5l, -0.5l), Point(-0.5l, 0.5l)

L, UL = Point(0.3l, 0.5l), Point(0.3l, -0.5l)

label("x = L", :S, L) label("x = 0", :S, zer) label("U(x)", :E, U)

label("U = ∞", :NW, Point(-0.5l, 0) ) label("U = 0", :NW, O)

label("U = ∞", :N, Point( 0.5l, 0) )

arrow(zer, X) arrow(zer, U) arrow(L, UL)

end 300 300 "lab1"

Для данных начальных условий решение стационарного уравнения Шрёдингера

примет вид:

In [1]: using Plots

┌ Warning: On Windows, creating file symlinks requires Administrator privileges └ @ Base.Filesystem file.jl:794

In [2]: function nrg(N, L = 10e-10) ħ = 6.626e-34/(2π) # J*s m = 9.1094e-31 # kg

q = 1.6022e-19 # Kl

E = [ 0.5(n*π*ħ/L)^2 /(m*q) for n = 1:N ]

plot()

for e in E

plot!([e,e], lab = "$(round(e, digits=3))", line = (3) )

end

yaxis!("E, eV")

end

# plot Probability

function ψ(n; L = 10e-10, plotP = false) x = [0:0.01L:L;]

k = π*n/L

S = sin.(k*x)

#plotP ? S = 2/L * S.^2 : S *= sqrt(2/L) plotP ? S = S.^2 : S # тернарный оператор

plot!(x, S, lab = "n=$n", line = (3), xaxis = ("x, A") )

end

Out[2]: ψ (generic function with 1 method)

In [3]: nrg(4) # построим 4 энергетических уровня для ямы шириной 10 ангстрем

Out[3]:

6

0.376

1.504

5 3.384

6.016

2

1

при увеличении ширины ямы, расстояния между энергетическими уровнями уменьшаются - спектр становится квазинепрерывным, и квантовая

Рассмотрим другие начальные условия:

In [34]: @png begin fontsize(18) l=200

X, U, zer = Point(0.5l, 0.5l), Point(-0.5l, -0.5l), Point(-0.5l, 0.5l)

L, UL = Point(0.3l, 0.5l), Point(0.3l, -0.5l)

label("x = a/2", :S, L) label("x = -a/2", :S, zer) label("U(x)", :E, U)

label("0", :SW, Point(0, 0.5l) ) label("U = ∞", :NW, Point(-0.5l, 0) ) label("U = 0", :NW, O)

label("U = ∞", :N, Point( 0.5l, 0) )

arrow(zer, X) arrow(zer, U) arrow(L, UL)

end 300 300 "lab1a"

In [27]: plot([2,2], [2,4], line = (:arrow, 3, :black), annotations=(2.02, 4, text("U(x)", :left)) ) plot!([1.75,3], [2,2], line = (:arrow, 3, :black), annotations=(2.6, 1.92, text("x = a/2", :down))) plot!([2.6,2.6], [2,4], line = (:arrow, 3, :black), leg=false, ticks=nothing, border=:none ) annotate!([(2.3, 3, text("U = 0", :center)), (2.75, 3, text("U = inf", :center)),

(1.8, 3, text("U = inf", :center)), (2, 1.92, text("x = -a/2", :down)) ])

Out[27]:

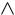U(x)

при четных n синус зануляется, а косинус заединичкивается =>

else

Чтоб найти константы C воспользуемся условием нормировки

In [96]: function Ψ(n; L = 10e-10, plotP = false)

k(n) = π*n/L

x = [-0.5L:0.01L:0.5L;]

cosin(n, x) = iseven(n) ? sin(k(n)*x) : cos(k(n)*x)

#plotP ? S = 2/L * cosin.(n, x).^2 : S = sqrt(2/L)*cosin.(n, x) plotP ? S = cosin.(n, x).^2 : S = cosin.(n, x)

plot!(x, S, lab = "n=$n", line = (3) )

end

Out[96]: Ψ (generic function with 1 method)

Кстати, n не может равняться нулю, так как волновая функция тогда бы всюду на промежутке (0…l) равнялась нулю! Это означает, что частица между стенками не может находиться в покое! Она обязательно должна двигаться. В аналогичных условиях находятся электроны проводимости в металле.

Полученный вывод распространяется и на них: электроны в металле не могут быть неподвижными.

Мы указали, что импульс электрона при отражении от стенок меняет знак. Поэтому на вопрос, каков импульс у электрона, когда он заперт между стенками, определённо ответить нельзя: то ли +p, то ли -p. Импульс неопределённый. Его степень неопределённости, очевидно, определяется так:

соотношение Гейзенберга в условиях нашей задачи, то есть при условии существования наименьшего значения p. Если же иметь в виду

произвольно-возможное значение импульса, то соотношение неопределённости получает следующий вид:

возможную при измерениях. Если в начале движения система была наделена минимальными неопределённостями, то с течением времени они могут расти.

Однако эта формула указывает и на другой чрезвычайно интересный вывод: оказывается, импульс системы в квантовой механике не всегда в состоянии изменяться непрерывно (как это всегда имеет место в классической механике). Спектр импульса частицы в нашем примере дискретный, импульс частицы между стенками может изменяться только скачками (квантами). Величина скачка в рассмотренной задаче постоянна и равна .

Например, для электрона при размерах ямы l =10e-1 м (свободные электроны в металле) ΔEn ≈ 10e-35 nДж ≈10e-16 nэВ, т.е. энергетические уровни расположены столь тесно, что спектр можно считать практически непрерывным. Если же размеры ямы соизмеримы с размерами атомов (l ≈10e-10 м), то для электрона ΔEn ≈10e-17 nДж ≈10e-2 nэВ, т.е. получаются явно дискретные значения энергии (линейчатый спектр). Таким образом, применение уравнения Шредингера к частице в потенциальной яме с бесконечно высокими стенками приводит к квантовым значениям энергии и координат, в то время как классическая механика на энергию этой частицы лишних ограничений не накладывает. Кроме того, квантово-механическое рассмотрение этой задачи приводит к выводу, что частица в потенциальной яме с бесконечно высокими стенками не может иметь энергию меньшую, чем минимальная энергия, равная

Обсудим подробнее вопрос о дискретности энергетического спектра. Разность энергий n-го и n+1-го энергетических уровней:

Как мы показали ранее, при увеличении ширины ямы (кстати, и массы) спектр становится всё менее дискретным. Стоит отметить, что и при увеличении n, дискретность спектра также играет меньшую роль из-за уменьшения соотношения

In [99]: ΔE_E = n-> (2n+1)/n^2 ΔE_E(10)

Out[99]: 0.21

In [101]: ΔE_E(200)

Out[101]: 0.010025

Этот результат является частным случаем принципа соответствия Бора, согласно которому законы квантовой механики должны при больших значениях квантовых чисел переходить в законы классической физики.

Более общая трактовка принципа соответствия: всякая новая, более общая теория, являющаяся развитием классической, не отвергает ее полностью, а включает в себя классическую теорию, указывая границы ее применимости, причем в определенных предельных условиях новая теория переходит в старую.

примеры+стенка

Тунельный

хороший учебник