Лебедев КММФЯ / Лебедев_4курс / 3_Barriers

Туннелирование электрона через потенциальную стенку

http://fn.bmstu.ru/data-physics/library/physbook/tom5/ch4/texthtml/ch4_3.htm

In [1]: using Plots

In [2]: plot([0,0], [0,1.5], line = (:arrow, 1, :black), annotations=(0.05, 1.5, text("U(x)", :left)) ) plot!([-1,1], [0,0], line = (:arrow, 1, :black), annotations=(1, 0.08, text("x", :up))) plot!([-0.7,0,0,1], [0,0,1,1], line = ( 3, :black), leg=false, ticks=nothing, border=:none )

annotate!([(-0.05, 1, text("U0", :right)), (2.4, 1.92, text("a", :center)),

(0, -0.05, text("0", :center)), (-0.5, 0.5, text("I")), (0.5, 0.5, text("II")) ])

Out[2]:

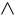U(x)

U0

I

II

x

0

Электрон падает слева на потенциальную стенку, имеющую конечную высоту . В случае				решения УШ будут иметь вид:

Иначе (частица над барьером):

В первом случае

из условия ограничения на бесконечности, во второй системе

, так как в области II над барьером нет отраженной

волны. Находим константы из условий непрерывности на границе:

Положим	, тогда		,		. Из анализа системы уравнений - Е может принимать любое значение (непрерывный спектр). ВФ

принимают вид:

И соответственно для

Физический интерес представляют коэффициенты отражения и прохождения, определяемые отношением плотностей потоков отраженных и прошедших через интерфейс электронов к плотности потока падающих на интерфейс электронов. Определим вектор плотности потока вероятности J следующим образом (в нашем одномерном случае это будет скаляр):

Тогда коэффициент прохождения D и коэффициент отражения R определяются следующим образом:

Вектора плотности вероятности для электронов:

- падающих из области I,

- отраженных в область I,

- прошедших в область II. При

:

В случае высокого порога вероятность прохождения нулевая, то есть частица полностью отражается. При

:

In [3]: #const ħ = 6.5821e-16 # eV*s const ħ = 1.0546e-34 # J*s const m = 9.1094e-31 # kg const q = 1.6022e-19 # Kl

k(E) = sqrt(2m*E*q)/ħ # 1/m

Out[3]: k (generic function with 1 method)

In [8]: function RD(U0 = 1.)

R(E) = E < U0 ? 1. : ( (1-sqrt(1-U0/E)) / (1+sqrt(1-U0/E)) )^2 D(E) = E < U0 ? 0. : 4sqrt(1-U0/E) / (1+sqrt(1-U0/E))^2

e = [0:0.01U0:2U0;]

plot(R, e, line = 3, lab = "R(E)") plot!(D, e, line = 3, lab = "D(E)")

title!("Transmission and Reflection coefficients")

end

Out[8]: RD (generic function with 2 methods)

In [9]: RD(5.)

Out[9]:

Transmission and Reflection coefficients

1.00
				R(E)
				D(E)
0.75
0.50
0.25
0.00
0.0	2.5	5.0	7.5	10.0

Правда занятно? Над барьером существует ненулевая вероятность отражения!

In [185]: function ψ(E::Array{Float64,1}, U0 = 1, a = 10e-10) # номер энерг-го ур-ня, ширина ямы

x1 = [-a:0.01a:0;]

x2 = [0.01a:0.01a:a;]

X = [x1;		x2] # конкатенация массивов
function		ElU(En)
k1	=	k(En)
k2	=	k(	abs(U0-En) )
A1	=	0.5 # из удобства отображения
A2	=	A1*2k1 / (k1+k2)
B2	=	A1*2k1 / (k1+im*k2)
ψ1(x) =			( A1*exp(im*k1*x) + B1*exp(-im*k1*x) ) |> abs2
ψ2(x) =			En > U0 ? A2*exp(im*k2*x) |> abs2 : B2*exp(-k2*x) |> abs2
B1	=	En	> U0 ? A1*(k1-k2) / (k1+k2) : A1*(k1-im*k2) / (k1+im*k2)

[ψ1.(x1); ψ2.(x2)]

end

# plot(x->0.5U0*(sign(x)+1), X, line = ( 3, :black), lab = "" ) plot([-a,0,0, a], [0,0,U0,U0], line = ( 3, :black), lab = "" )# так проще hline!(E, lab = "") # барьер и уровни энергии

for En in E

plot!(X, ElU(En).+En, line = 3, lab = "E = $En eV" )

end

yaxis!("E, eV", (0, maximum(E)+1) ) xaxis!("x, A")

end

Out[185]: ψ (generic function with 6 methods)

In [186]:	ψ([1., 4., 6., 8.], 5.)
Out[186]:	9
								E = 1.0 eV
								E = 4.0 eV
								E = 6.0 eV
								E = 8.0 eV
	6
	E, eV
	3
	0	- 9		- 10	0		- 10		- 9
	- 1×10		- 5×10			5×10		1×10
					x, A

Туннелирование электрона через потенциальный барьер

In [90]: plot([0,0], [0,1.5], line = (:arrow, 1, :black), annotations=(0.05, 1.5, text("U(x)", :left)) ) plot!([-0.5,1], [0,0], line = (:arrow, 1, :black), annotations=(1, 0.08, text("x", :up))) plot!([-0.4,0,0,0.5,0.5,1], [0,0,1,1,0,0], line = ( 3, :black), leg=false, ticks=nothing, border=:none )

annotate!([(-0.05, 1, text("U0", :right)), (2.4, 1.92, text("a", :center)), (0.5, -0.05, text("a", :center)),

(0, -0.05, text("0", :center)), (-0.25, 0.5, text("I")), (0.25, 0.5, text("II")), (0.75, 0.5, text("III")) ])

Out[90]:

U(x)

U0

I

II

III

x

0

a

По аналогии с предыдущими задачами, находим решение УШ для каждой области.

Для :

Примем

, а

так как в области III нет отраженной волны де Бройля. Используем условия сшивки для х = 0 и х = а:

И для

:

Эти системы имеют решения при любых значениях E (энергетический спектр частицы является непрерывным). Основное внимание в данной задаче

можно сосредоточить на анализе прохождения частицы через барьер (поведение в области III), для этого достаточно выразить

через

. Ай, да и

все остальные тоже найдем:

In [91]: using Reduce, Latexify

Reduce (Free CSL version, revision 4534), 05-Apr-18 ...

In [178]: exprn = ( :( A_1+B_1-A_2-B_2 ),

:( im*k_1*A_1 - im*k_1*B_1 - k_2*A_2 + k_2*B_2 ),

:( A_2*e^(k_2*a) + B_2*e^(-k_2*a) - A_3*e^(im*k_1*a) ),

:( k_2*A_2*e^(k_2*a) - k_2*B_2*e^(-k_2*a) - im*k_1*A_3*e^(im*k_1*a) ) )

exprn2 = ( :( A_1+B_1-A_2-B_2 ),

:( im*k_1*A_1 - im*k_1*B_1 - im*k_2*A_2 + im*k_2*B_2 ),

:( A_2*e^(im*k_2*a) + B_2*e^(-im*k_2*a) - A_3*e^(im*k_1*a) ),

:( im*k_2*A_2*e^(im*k_2*a) - im*k_2*B_2*e^(-im*k_2*a) - im*k_1*A_3*e^(im*k_1*a) ) )

vars = (:B_1, :A_2, :B_2, :A_3)

latexify([e for e in exprn2], transpose = true)

Out[178]:

In [179]: sol = Algebra.solve( exprn, vars) solarr = [s for s in sol]

sol2 = Algebra.solve( exprn2, vars) solarr2 = [s for s in sol2]

Out[179]: 4-element Array{Expr,1}:

:(b_1 =		((1 - ^ (2 * a		* im * k_2)) * (k_1 ^ 2 - k_2 ^ 2) * a_1) / ((k_1 ^ 2 + 2 * k_1 * k_2 + k_2 ^				2) - ^ (2 * a * im * k
_2) * ((k_1			^ 2 - 2 * k_1	* k_2) + k_2	^ 2)))
:(a_2	=	(2	* (k_1 + k_2)	* a_1 * k_1)	/ ((k_1 ^ 2 + 2 * k_1 * k_2 + k_2 ^ 2) - ^ (2 * a * im * k_2) * ((k_1 ^ 2 - 2 * k_1 * k
_2) + k_2 ^			2)))					- ^ (2 * a * im * k_2)
:(b_2	=	(-2 * ^ (2 * a		* im * k_2) * (k_1		- k_2)	* a_1 * k_1) / ((k_1 ^ 2 + 2 * k_1 * k_2 + k_2 ^ 2)
* ((k_1 ^ 2			- 2 * k_1 * k_2) + k_2 ^ 2)))				/ ( ^ (a * im * k_1) * ((k_1 ^ 2 + 2 * k_1 * k_2 + k_2 ^ 2) - ^ (2 * a *
:(a_3	=	(4	* ^ (a * im	* k_2) * a_1 * k_1		* k_2)
im * k_2) *			((k_1 ^ 2 - 2	* k_1 * k_2)	+ k_2 ^ 2))))

In [180]: latexify(solarr2, transpose = true)

Out[180]:

почему е не отображается

In [279]: funs = [:B1, :A2, :B2, :A3, :uB1, :uA2, :uB2, :uA3]

Sols = [solarr; solarr2]

funhead(funame) = :( $funame(k_1, k_2, a, a_1) ) for i = 1:8

Expr(:function,funhead(funs[i]), Sols[i] ) |> eval

end

funevl = [eval(fun) for fun in funs]

Out[279]: 8-element Array{Function,1}: B1

A2

B2

A3

uB1

uA2

uB2

uA3

Теперь у нас есть функции считающие константы для волновых функций под и над барьером. Найдем вектор плотности потока вероятности для падающей на барьер и прошедшей через него волны, а также коэффициент прохождения:

Очевидно, что , но если есть желание можете и посчитать...

In [219]: function RDb(U0 = 1., a = 10e-10)

a1 = 1.

e = [0:0.01U0:3U0;]

D(E) = E < U0 ? abs2( A3(k(E), k(U0-E), a, a1) ) : abs2( uA3(k(E), k(E-U0), a, a1) ) R(E) = 1.0 - D(E)

plot(R, e, line = 3, lab = "R(E)") plot!(D, e, line = 3, lab = "D(E)") vline!([U0], lab = "")

title!("Transmission and Reflection coefficients")

# дырочки (разрывы) можно залатать при E=U0: D = 2ħ^2 / (2ħ^2 + m*a^2*U0)

end

Out[219]: RDb (generic function with 3 methods)

In [220]: RDb(2.)

Out[220]:

Transmission and Reflection coefficients

	1.00
							R(E)
							D(E)
	0.75
	0.50
	0.25
	0.00
	0	1	2	3	4	5	6
In [267]:	function Ψ(E::Array{Float64,1}, U0 = 5., a = 10e-10, A1 = 0.5) # номер энерг-го ур-ня, ширина ямы
	x1 = [-a:0.01a:0;]
	x2 = [0.01a:0.01a:a;]
	x3 = [1.01a:0.01a:2a;]
	X = [x1; x2; x3] # конкатенация массивов
	function ElU(En)
	k1 = k(En)
	k2 = k( abs(U0-En) )
	itr = 1:4
	j = 1
	if En > U0
	itr = 5:8
	j = im
	end
	C = [ fun(k1, k2, a, A1) for fun in funevl[itr] ]
	ψ1(x) = ( A1*exp(im*k1*x) + C[1]*exp(-im*k1*x) ) |> abs2
	ψ2(x) = ( C[2]*exp(j*k2*x) + C[3]*exp(-j*k2*x) ) |> abs2
	ψ3(x) = C[4]*exp(im*k1*x) |> abs2
	[ψ1.(x1); ψ2.(x2); ψ3.(x3)]
	end
	plot([-a,0,0,a,a,2a], [0,0,U0,U0,0,0], line = ( 3, :black), lab = "" ) # барьер
	hline!(E, lab = "") # барьер и уровни энергии

for En in E

plot!(X, ElU(En).+En, line = 3, lab = "E = $En eV" )

end

yaxis!("E, eV", (0, maximum(E)+2) ) xaxis!("x, A")

end

Out[267]: Ψ (generic function with 4 methods)

In [268]:	Ψ([1.,3.,5.1,7.])
Out[268]:		9
								E = 1.0 eV
								E = 3.0 eV
								E = 5.1 eV
								E = 7.0 eV
		6
	E, eV
		3
		0	- 9		0		- 9			- 9
		- 1×10				1×10		2×10
						x, A
In [278]:	Ψ([5., 13., 19.8], 20, 1e-10, 1.5)
Out[278]:
		20						E = 5.0 eV
								E = 13.0 eV
								E = 19.8 eV
		15
	E, eV	10
		5
		0		- 10	0		- 10		- 10
		- 1×10				1×10		2×10
						x, A