1. Механика Галилея—Ньютона называется классической механикой. В ней изучаются законы движения макроскопических тел, скорости которых малы по сравнению со скоростью света с в вакууме. Законы движения макроскопических тел со скоростями, сравнимыми со скоростью с, изучаются релятивистской механикой, основанной на специальной теории относительности, сформулированной А. Эйнштейном (1879—1955). Для описания движения микроскопических тел (отдельные атомы и элементарные частицы) законы классической механики неприменимы — они заменяются законами китовой механики. Механика делится на три раздела: I) кинематику; 2) динамику; 3) статику.

2. Динамические уравнения движения материальной точки:

Динамика - это раздел теоретической механики, в котором механическое движение изучают, учитывая силы, вызвавшие движение. Первая из них (прямая задача динамики) заключается в том, что по известному движению находят силы, вызвавшие движение.

Вторая задача (обратная задача динамики) состоит в том, что по известным силам определяют движение.

Первая аксиома динамики (аксиома инерции). Существуют такие системы отсчета, в которых изолированная материальная точка остается в состоянии покоя или равномерного прямолинейного движения.

Вторая аксиома динамики (основная аксиома динамики).

Эту аксиому также называют основным законом механики или вторым законом Ньютона.

В инерциальной системе отсчета ускорение материальной точки пропорционально силе, приложенной к ней: ma = F

Третья аксиома динамики (аксиома действия и противодействия).Эту аксиому также называют третьим законом Ньютона. Две материальные точки взаимодействуют друг с другом с силами, равными по величине, направленными по одной прямой в разные стороны.

3. Количество движения точки. Импульс силы

Количество движения, мера механического движения, равная для материальной точки произведению её массы m на скорость v. К. л. mv - величина векторная, направленная так же, как скорость точки.

И́мпульс (Количество движения) — векторная физическая величина, характеризующая меру механического движения тела. В классической механике импульс тела равен произведению массы m этой точки на её скорость v, направление импульса совпадает с направлением вектора скорости:

4. Теорема об изменении количества движения

Изменение количества движения точки за некоторый промежуток времени равно импульсу силы, действующему на точку в течение того же промежутка времени.

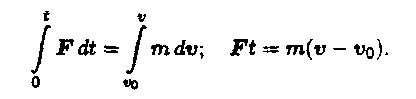
5. теорема об изменении кинетической энергии точки

Пусть точка с массой m в начальный момент t = 0 находится в положении и имеет скорость , а в момент , в положении и имеет скорость .

Выберем систему координат и спроектируем основное уравнение (13.2.2) на касательную

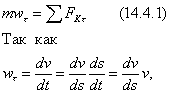
Это теорема об изменении кинетической энергии в дифференциальной форме.Проинтегрировав уравнение (14.4.5), получим туже теорему в конечном виде:

6. Работа силы. Работа силы тяжести и силы упругости

Элементарная работа dA = Ftds, Ft — проекция силы на касательную к траектории, направленная в сторону перемещения, или dA = Fdscosa.

Если a — острый, то dA>0, тупой — <0, a=90o: dA=0. dA= — скалярное произведение вектора силы на вектор элементарного перемещения точки ее приложения; dA= Fxdx+Fydy+Fzdz — аналитическое выражение элементарной работы силы. Работа силы на любом конечном перемещении М0М1: . Если сила постоянна, то = F×s×cosa. Единицы работы:[1 Дж (джоуль) = 1 Нм]. , т.к. dx= dt и т.д., то .

Теорема о работе силы: Работа равнодействующей силы равна алгебраической сумме работ составляющих сил на том же перемещении А=А1+А2+…+Аn.

Работа силы тяжести: , >0, если начальная точка выше конечной.

Работа силы упругости: —работа силы упругости равна половине произведения коэффициента жесткости на разность квадратов начального и конечного удлинений (или сжатий) пружины.

7. Механическая система. Масса системы. Центр масс системы

Масса системы. Центp масс. Движение системы, кpоме действующих сил, зависит также от ее суммаpной массы и pаспpеделения масс. Масса системы pавна аpифметической сумме масс всех точек или тел, обpазующих систему М = ∑mк.

Ц е н т p о м м а с с системы называется геометpическая точка С, pадиус-вектоp котоpой

(1.117)

В пpоекциях на декаpтовы оси кооpдинат это pавенство запишется

, , (1.118)

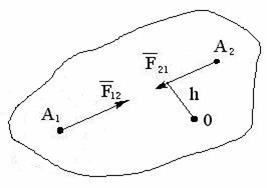
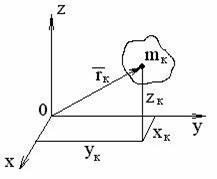
Рис. 1.87 Рис. 1.88

Понятие «центр масс» является очень важным. При исследовании движения системы очень часто невозможно определить движение каждой из точек системы. Поэтому, о движении системы судят по движению ее центра масс.

8. Теорема о движении центра масс системы.

Произведение массы системы на ускорение ее центра масс равно геометрической сумме всех действующих на систему внешних сил 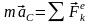– дифференциальное уравнение движения центра масс. В проекциях на оси координат: .

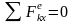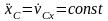Закон сохранения движения центра масс. Если главный вектор (векторная сумма) внешних сил остается все время равным нулю, то центр масс механической системы находится в покое или движется прямолинейно и равномерно. Аналогично в проекциях на оси, если Þ , если при этом в начальный момент v_Cx0= 0, то Þ 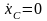Þ x_C= const.

Количество движения системы Q (иногда обозначают К) – вектор, равный геометрической сумме (главному вектору) количеств движения всех точек системы:

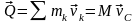, М – масса всей системы, v_C – скорость центра масс.

9. Теорема об изменении количества движения системы: 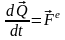– производная по времени от количества движения механической системы геометрически равна главному вектору внешних сил, действующих на эту систему. В проекциях: 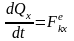, и т.д. Теорема об изменении кол-ва движения системы в интегральной форме:

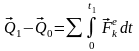, где 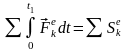– импульсы внешних сил.

В проекциях: Q_1x – Q_0x = åS^e_kx и т.д. количество движения системы за некоторый промежуток времени равно сумме импульсов действующих на систему внешних сил за тот же промежуток времени. Закон сохранения количества движения – если сумма всех внешних сил, действующих на систему, = 0, то вектор количества движения системы будет постоянен по модулю и направлению: Þ 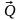= const, аналогично в проекциях: Þ Q_x= const. Из закона следует, что внутренние силы изменить суммарное количество движение системы не могут. Тело переменной массы , масса которого непрерывно изменяется с течением времени m= f(t) (пр.: ракета, топливо которой убывает). Дифф-ное уравнение движения точки переменной массы:

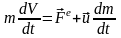– уравнение Мещерского, u – относительная скорость отделяющихся частиц. 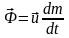– реактивная сила, 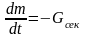— секундный расход топлива, 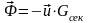. Реактивная сила направлена в противоположную сторону относительной скорости истечения топлива.

10. Дифф-ные ур-ния вращения твердого тела вокруг неподвижной оси: ,

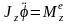J_z – момент инерции тела относительно оси вращения z, 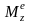– момент внешних сил относительно оси вращения (вращающий момент). 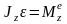_, e – угловое ускорение, чем больше момент инерции при данном _, тем меньше ускорение, т.е момент инерции при вращательном движении является аналогом массы при поступательном. Зная _, можно найти закон вращения тела j=f(t), и, наоборот, зная j=f(t), можно найти момент. Частные случаи: 1) если = 0, то w = const – тело вращается равномерно; 2) = const, то e = const – вращение равнопеременное. Уравнение аналогичное дифф-ному уравнению прямолинейного движения точки .

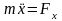11. Радиус инерции. Основные моменты инерции некоторых однородных тел

Радиусом инерции тела относительно данной оси z называется линейная величина , определяемая равенством , где М- масса системы. )Моментом инерции твердого тела относительно оси называется скалярная величина, равная сумме произведений массы каждой точки тела на квадрат расстояния от этой точки до оси.

Моментом инерции твёрдого тела относительно плоскости называется скалярная величина, равная сумме произведений массы каждой точки тела на квадрат расстояний от этой точки до плоскости.

Моментом инерции твёрдого тела относительно полюса (полярным моментом инерции) называется скалярная величина, равная сумме произведений массы каждой точки тела на квадрат расстояния от точки до этого полюса.