1.2 Двумерные случайные величины

Пусть нам дана дискретная двумерная случайная величина Z(X,Y), геометрически каждое ее значение может быть представлено точкой на плоскости (X,Y). При этом каждая из ее координат также является дискретной случайной величиной.

Как мы знаем из теории вероятностей, полное описание такой случайной величины задается таблицей вероятностей p_ij. Т.е. мы предполагаем, что нам известен набор возможных значений дискретных случайных величин Х и Y: {x_i} и {y_j}, тогда p_ij есть вероятность сложного события, состоящего в том, что в одном опыте одновременно величина X примет значение x_i, а величина Y примет значение y_j ¹².

При сделанных предположениях мы можем вычислить характеристики всех упомянутых случайных величин.

M[X] = µ_x = D_x = (1.6)

M[Y] = µ_y = D_y =

Как известно, для двумерной случайной величины помимо двух дисперсий D_x и D_y существует еще один центральный момент второго порядка – корреляционный момент:

(1.7)

Этот момент отражает наличие некоторой связи между случайными величинами X и Y, если они независимы, то σ_ху равен нулю. Отметим, что обратное вообще говоря неверно: из того, что = 0, не следует, что величины непременно независимы, они могут оказаться зависимыми; такие величины называют некоррелированными.

В статистике мы не располагаем вероятностями, но мы предполагаем, что вероятности однозначно связаны с частотами для генеральной совокупности, а именно ; здесь n_ij – количество случаев в генеральной совокупности, в которых случайная величина X = x_i , а Y = y_j. Таким образом, для характеристик генеральной совокупности получим выражения:

(1.8)

Однако и данными о генеральной совокупности мы располагаем редко, потому приведенные формулы имеют скорее теоретическую ценность. Чаще всего мы располагаем только выборочными данными. Причем обычно в ходе получения этих выборочных данных мы проводим n испытаний, в каждом из которых определяется одно значение двумерной случайной величины z_i = (x_i,y_i), т.е. тут i уже не номер одного из возможных значений дискретной случайной величины, а номер опыта, в ходе которого устанавливаются значения двумерной величины z_i. Таким образом, мы располагаем одинаковым количеством одинаково нумерованных значений x_i и y_i, которые получены в ходе i-го измерения.

Для выборочных данных мы получим такие формулы:

(1.9)

(1.10)

Напомним, что здесь, как и в иных случаях, символами , мы будем обозначать выборочные средние, в отличие от генеральных средних µ_х и µ_у.

Соответственно, Var(x), Var(y), Cov(x,y) мы будем называть центральные моменты второго порядка, рассчитанные для выборки. Напомним, что все они являются смещенными оценками¹³ соответствующих моментов для генеральной совокупности:

M[Var(x)] = M[Var(y)] = M[Cov(x,y)] = ¹⁴

1.2.1 Правила вычислений моментов второго порядка

Напомним основные правила вычисления центральных моментов второго порядка:

1. Var(X) = Cov(X,X)

2. Если X = b = const то Var(X) = 0

3. Если X = b Y то Var(X) = b² Var(Y) (1.11)

4. Если X = b + Y то Var(X) = Var(Y)

5. Если X = V + Y то Var(X) = Var(Y) + Var(V) + 2 Cov(V,Y)

Кроме того, часто бывают полезны следующие формулы (они позволяют сократить объём необходимых вычислений):

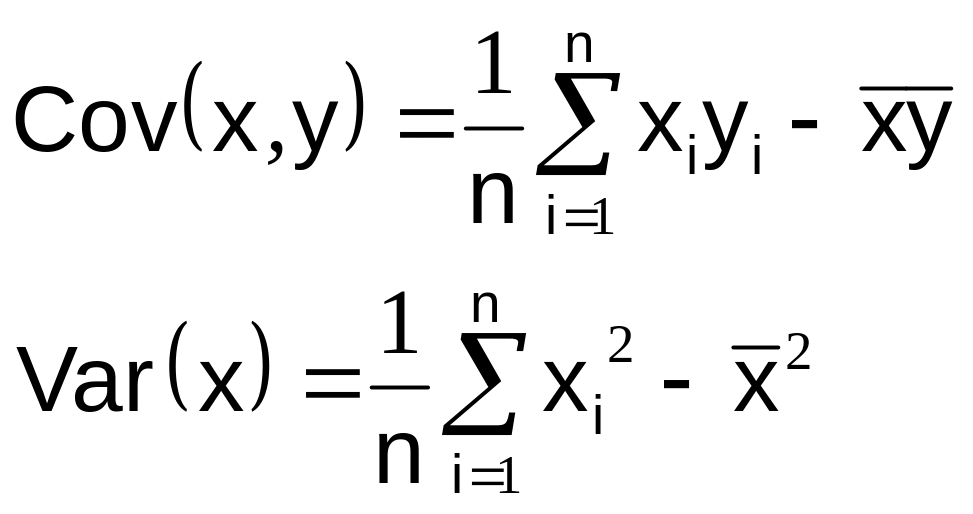(1.12)

Важное замечание. Мы привели формулы для вычислений моментов по выборочным данным. Однако поскольку природа указанных формул чисто алгебраическая, они сохраняют свою силу и для генеральной совокупности, и для непрерывных случайных величин. Например, для произвольной двумерной случайной величины справедливо утверждение, аналогичное формуле 3 из (1.11), а именно:

если X и Y случайные величины, причем X = b Y , то ¹⁵