1.1.10 Критерий χ-квадарат.
Итак, проблема а) из пункта 6 нами разобрана, проблему б) мы пока отложим и перейдем к рассмотрению проблемы в) – проблемы соответствия эмпирического распределения теоретическому закону.
Для решения этой проблемы разработан целый спектр различных методов, но наиболее широко употребительным является метод, получивший название критерия χ-квадарат (читается: хи-квадрат). Он применяется для установления подобия данного эмпирического распределения некоему теоретическому, но мы рассмотрим проблему в конкретном случае: можно ли считать данное эмпирическое распределение нормальным или нет?
Нам нужно выяснить, можно ли считать9 закон распределения некоей случайной величины (например, зарплаты выпускников МСУ спустя 3 года после окончания ВУЗа) нормальным или нет?
Решение такой задачи можно представить в виде такой последовательности шагов.
1. Проводим серию опытов, в результате получаем выборку значений нашей случайной величины объёмом в N значений (возможно, уже вначале мы располагаем данными о подобной выборке)
2. Осуществляем классификацию данных, т.е.разбиваем все имеющиеся данные на группы (классы). Группу образуют данные, принадлежащие некоторому выбранному нами интервалу значений. При этом следует проводить разбиение всего диапазона значений случайной величины таким образом, чтобы в каждом классе оказалось не менее 5-ти представителей, и чтобы общее число классов было не менее 4-х. Заметим, что не обязательно разбивать весь диапазон значений на равные интервалы. Так для задачи классификации выпускников по зарплате можно выбрать следующие интервалы:
< 1800, 1800 ÷ 2400, 2400 ÷ 3200, 3200 ÷ 4300, 4300 ÷ 5800, > 5800
Как нетрудно заметить, ширина интервала в этом примере составляет примерно треть от величины левого края интервала, значит, ширина растет в геометрической прогрессии, что достаточно характерно для экономических задач.
После проведения классификации всем элементам класса присваивается одно и то же значение, равное середине соответствующего интервала. Некоторое исключение делается для крайних интервалов, которые полубесконечны. Элементам этих приписывается значение, равное краю интервала (справа это минимум значений, а слева – максимум) ± полуширина соседнего интервала («+» выбирается для крайнего правого, а «–» для крайнего левого значения; именно такие значения используют для элементов полубесконечных интервалов при вычислении среднего и дисперсии.
3. Подсчитываем количество
представителей в каждом из интервалов
и обозначаем их ni,
здесь – номер соответствующего
интервала. Вычисляем основные
характеристики нашей случайной величины
по формулам:
,
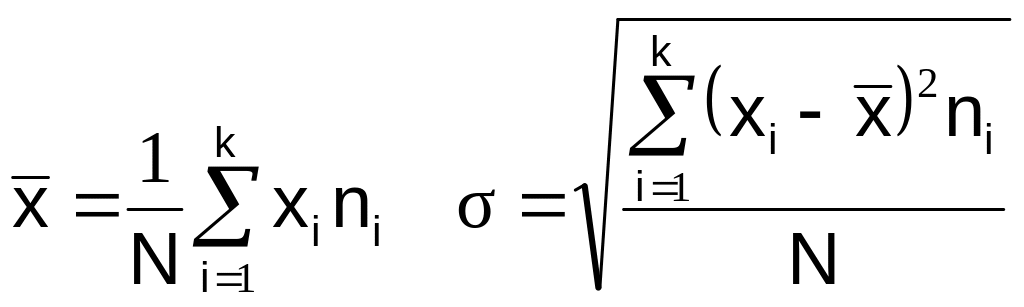здесь N
– объём выборки, хi
– центр i–го интервала, ni
– количество представителей в интервале,
а k
– количество интервалов разбиения.
4. Теперь, зная и σ, мы можем приступить к вычислению характеристик теоретического распределения.
Представим себе, что мы произвели ровно столько же измерений (N) для еще одной случайной величины (назовём её теоретической). Эта величина характеризуется тем, что она распределена в строгом соответствии с нормальным законом распределения и притом имеет в точности те же самые характеристики (матожидание и дисперсию), что и наш набор выборочных данных.
Сколько при таких обстоятельствах было бы представителей у такой случайной величины в каждом из наших интервалов?
Чтобы ответить на этот вопрос, найдем вероятности рi попадания теоретической случайной величины в i–й интервал – для всех интервалов, естественно крайние интервалы считаются полубесконечными. Это вполне можно сделать, т.к. мы располагаем матожиданием и σ, а также предполагаем, что случайная величина строго следует нормальному закону распределения, – как обычно, находим вероятности рi используя функцию Лапласа
А уже располагая величинами
рi,
мы можем вычислить для теоретической
случайной величины и количество попаданий
в те же интервалы. Для этого нужно
умножить вероятности рi
на общее число замеров, которые мы
произвели (на объём выборки):
и округлить полученные величины до
ближайших целых значений.
5. Теперь мы располагаем двумя наборами частот попаданий в наши интервалы: мы имеем реальные величины10 ni и теоретические величины . Как и следовало ожидать, между ними наблюдаются определенные различия. И мы опять оказываемся перед дилеммой: наблюдаемые различия носят случайный характер или вызваны тем, что распределение эмпирической случайной величины не является нормальным?
Вполне очевидно, что перед нами классическая ситуация нулевой гипотезы, и нулевая гипотеза состоит в том, что расхождения теоретического и эмпирического распределений носит случайный характер.
А количественно оценить различия нам поможет критерий χ-квадарат.
Вычислим величину критерия по формуле:
(1.5)
а также число степеней свободы f = k – 311
6. Теперь посмотрим в таблицы критерия χ-квадарат. Они имеют два входа: число степеней свободы и уровень значимости, обычно приведены данные для двух уровней значимости: 5% и 1%.
Далее по обычной схеме:
- если вычисленное нами значение критерия χ-квадарат для нашего числа степеней свободы f меньше того, что дает 5%-ный уровень значимости, то нулевая гипотеза принимается.
- если вычисленное нами значение критерия χ-квадарат для нашего числа степеней свободы f больше того, что дает 1%-ный уровень значимости, то нулевая гипотеза отвергается.
- если вычисленное значение критерия лежит между двумя табличными значениями, ситуация рассматривается как неопределенная.
Т.е. в первом случае (нулевая гипотеза принимается) мы вопрос о соответствии данного эмпирического распределения теоретическому распределению решаем в положительном смысле: у нас нет оснований полагать, что эмпирическое распределение отлично от теоретического, а все наблюдаемые расхождения вполне объяснимы случайными причинами.
Во втором случае у нас есть основания полагать, что расхождение между теоретическим и эмпирическим распределениями существенно, и объяснить его только случайными расхождениями нельзя.