2.1.7 Оценки ошибок коэффициентов регрессии

Напомним, что при вычислении коэффициентов регрессии мы исходим из предположения, что в каждом наблюдении величина y_j состоит из двух компонент: 1)неслучайной составляющей ₁ + ₂ x_i и 2)случайного члена u_i: y_i = ₁ + ₂ x_i + u_i (2.1).

В результате мы получаем представление случайной величины Y в виде , причем . Заметим, что в силу предположения о наличии случайной составляющей u в составе величины Y, найденные нами коэффициенты регрессии тоже являются случайными величинами. Соответственно, возникает задача оценить стандартные ошибки для этих случайных величин, построить доверительные интервалы и т.п.

Если исходить из того, что нам известна дисперсия случайной составляющей u в составе величины Y, то для вычисления величин стандартных отклонений коэффициентов регрессии можно получить следующие выражения:

(2.10)

Из приведенных выражений следуют очевидные заключения.

Во-первых, дисперсии коэффициентов регрессии обратно пропорциональны количеству наблюдений в выборке.

Во-вторых, дисперсии коэффициентов прямо пропорциональны дисперсии случайного члена и обратно пропорциональны дисперсии Х. Дело в том, что наблюдаемые изменения величины Y отчасти вызваны изменениями Х, а отчасти случайным членом u. И чем меньше вариация Х, тем большая доля в изменении объясняемой величины порождена именно случайным членом; соответственно тем больше будет и дисперсия коэффициентов регрессии. Как видим, важны не абсолютные значения величин и Var(X), а их отношение: чем оно больше, тем большая доля в изменении Y порождена случайными причинами. Соответственно, тем большей окажется и дисперсия коэффициентов регрессии.

В реальной ситуации мы разумеется не можем знать величину , но мы можем построить ее оценку. Если мы провели прямую регрессии, значит нам уже известны величины ε_i = y_i – , следовательно мы можем вычислить вариацию Var(ε). Тогда несмещенная оценка дисперсии случайного члена u примет вид:

(2.11)

При этом вариацию Var(ε) следует умножить на корректирующий множитель , т.к. число степеней свободы при вычислении характеристик коэффициентов линейной регрессии составляет n–2 (мы уже знаем два коэффициента).

Теперь располагая оценкой (2.11) мы можем получить несмещенные оценки дисперсии коэффициентов регрессии:

(2.12)

где вычисляется по формуле (2.11). Корни квадратные из величин и называются стандартными отклонениями коэффициентов регрессии:

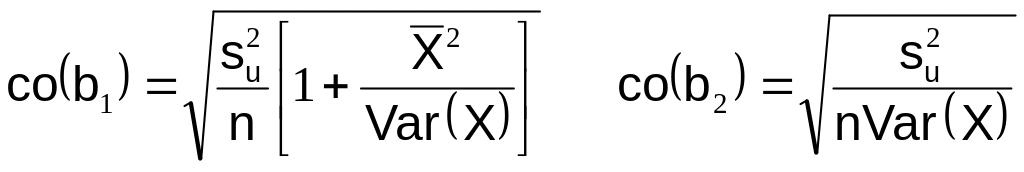(2.13)

2.1.8 Проверка гипотез для коэффициентов регрессии

Располагая оценками величин дисперсии коэффициентов регрессии мы можем обычным образом построить механизм проверки достоверности гипотез, относящихся к значениям коэффициентов регрессии.

Рассмотрим гипотетический пример. Пусть в течении последних 5-ти лет темп роста производительности труда составил t процентов в год, а зарплата росла опережающими темпами Х процентов в год, W = X – t >0. Мы выдвинули гипотезу, что темп роста инфляции Y определяется именно опережающим темпом роста зарплат, причем мультипликатор ₂ равен 1,5; это эквивалентно предположению, что Y = ₁ + 1,5 Х .

Построив уравнение регрессии, мы получили, что Y = b₁ + 1,77 W. Противоречат наши данные выдвинутой гипотезе или нет?

Заметим, что если случайный член нашей зависимости удовлетворяет условиям Гаусса-Маркова, то коэффициенты линейной регрессии также будут нормально распределенными величинами. В соответствии с общими принципами оценки достоверности гипотез мы вычислим параметр z : ¹⁸

Если значение параметра z по модулю не превосходит стандартного значения 1,96 (–1,96 z  1,96), которое отвечает 5% уровню значимости для нормально распределенных величин, мы заключаем, что у нас нет оснований отвергнуть нулевую гипотезу и что отклонение полученного значения коэффициента 1,77 от теоретического 1,5 вызвано случайными факторами.

Если значение параметра z по модулю превосходит стандартное значение 2,58, которое отвечает 1% уровню значимости для нормально распределенных величин, мы заключаем, что у нас нет оснований принять нулевую гипотезу и что отклонение полученного значения коэффициента 1,77 от теоретического 1,5 вызвано неадекватностью нашей гипотезы.

Как обычно, получение значения в интервале между 1,96 и 2,58 требует принятия волевого решения.

Заметим, что при сравнительно небольших объемах выборки вместо значений 1,96 и 2,58 следует пользоваться таблицами распределения Стьюдента, принимая число степеней свободы в случае линейной регрессии равным n–2. В этом случае значение параметра сравниваются со значениями t_крит , которые соответствуют 5%-ному и 1%-ному уровню значимости критерия Стьюдента для нашего значения числа степеней свободы.