Д И Н А М И К А С У Д Н А

МОДУЛЬ 8.7

7.3 Учет влияния скорости хода на продольную качку корабля на тихой воде

Скорость хода влияет на продольную качку двояко:

1. изменяется обтекание корабля из-за появления продольных составляющих скорости и изменяется вследствие этого давление на смоченной поверхности корабля;

2. изменяется вертикальная скорость обтекания каждой шпангоутной рамки. В соответствии с рис.1 при наклонении корабля на угол 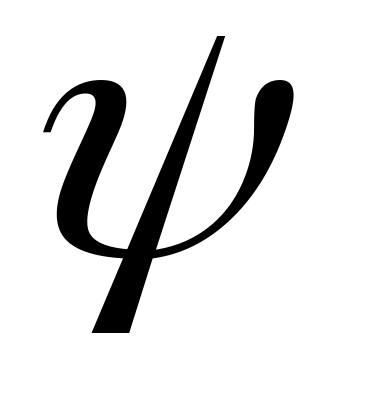появляется составляющая скорости 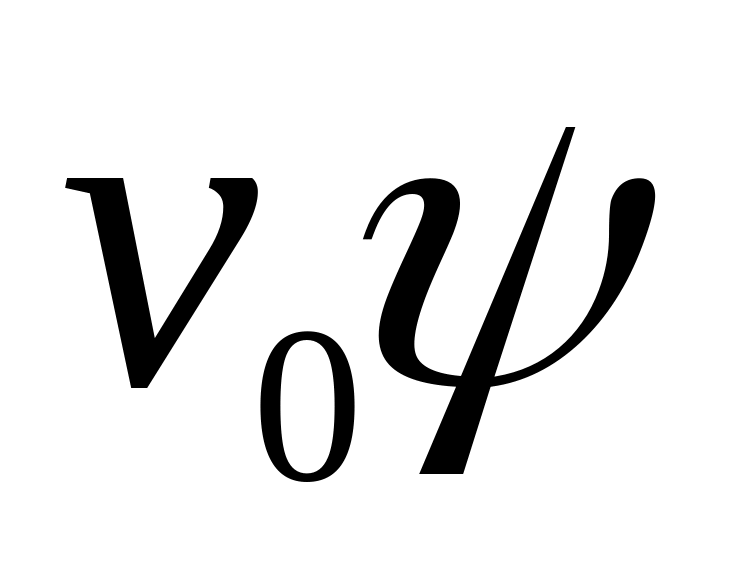, так что скорость обтекания отсека будет равна 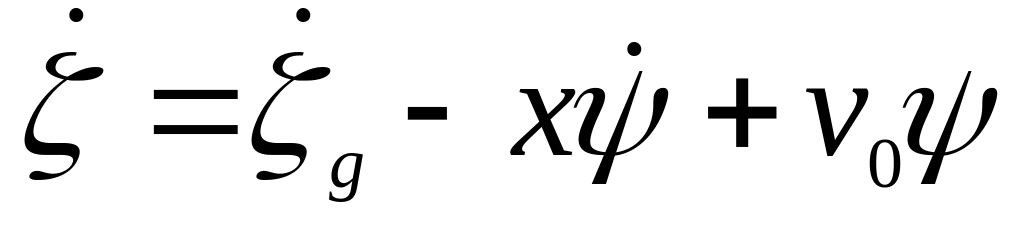, а ускорение .

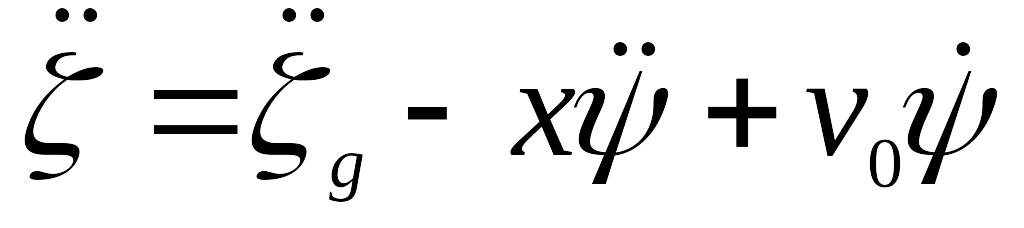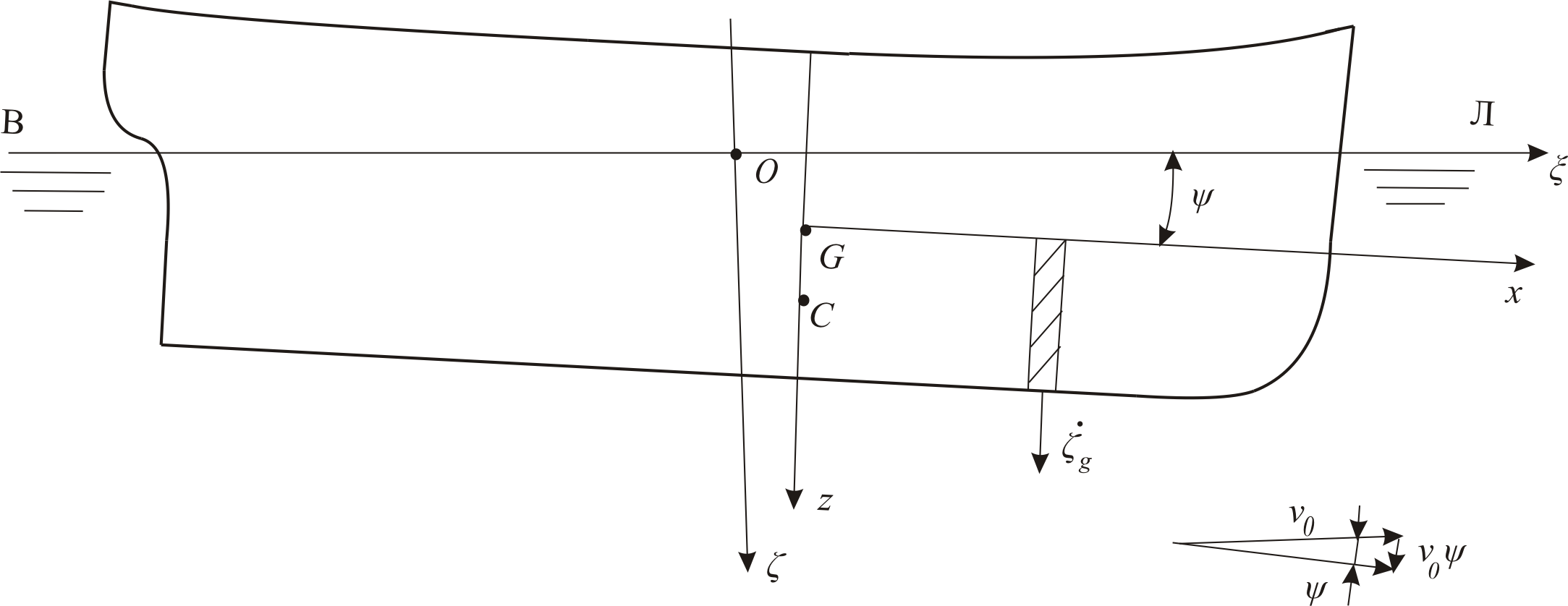
Рис. 1. Определение дополнительной скорости обтекания шпангоута

После всех преобразований уравнения продольной качки на тихой воде с учетом скорости хода будут иметь вид:

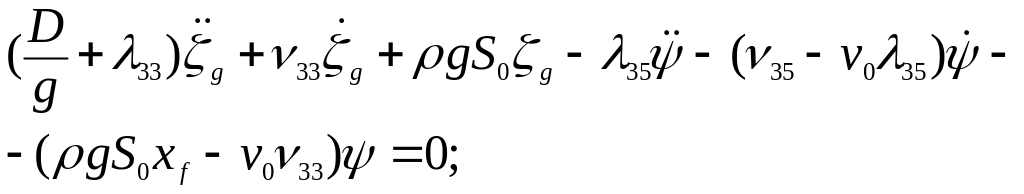
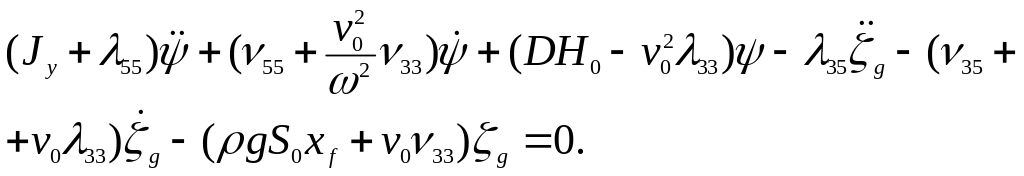(1)

Если корабль будет симметричным относительно мидельшпангоута, ; и уравнения несколько упростятся, но при наличии скорости не разделятся

(2)

7.4. Уравнения продольной качки корабля на встречном волнении без скорости хода

Для встречного волнения курсовой угол и уравнение волновой поверхности можно записать в виде:

.

При выводе сил, действующих на отсек при качке, можно использовать примененный ранее принцип относительного движения. Отсек переместится на расстояние со скоростью и ускорением . Соответственно силы гидромеханической природы будут равны:

.

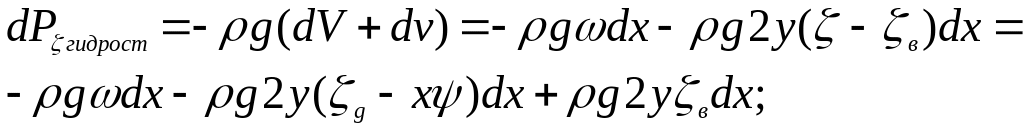
Таким образом, в выражениях для сил по сравнению с тихой водой присутствуют члены, зависящие от волнения. Их можно объединить как возмущающие

,

а затем проинтегрировать отдельно для всего корабля

. (3)

Подставим в (3)

(4)

Тогда получим

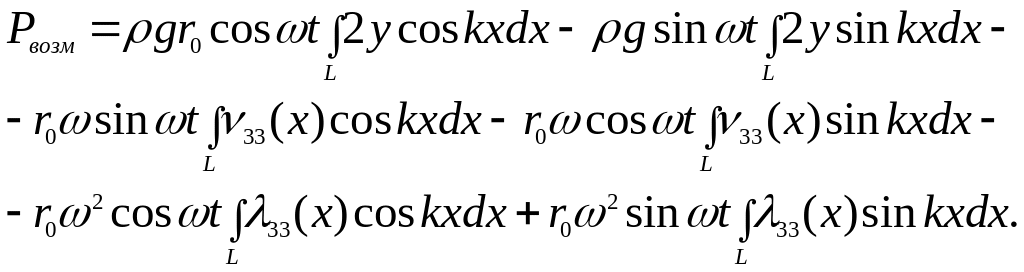(5)

Для возмущающего момента можно записать

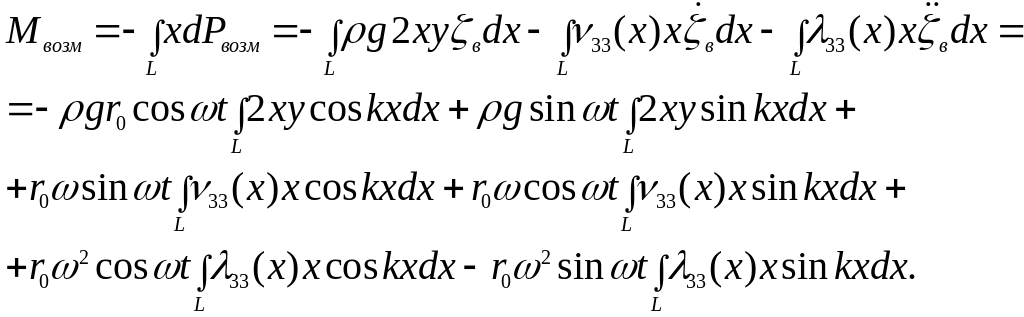(6)

Введем обозначения

; ;

; ;

; ;

; ;

; ;

(7)

Уравнения качки корабля на волнении будут отличаться от уравнений качки на тихой воде наличием в правых частях возмущающих сил и моментов. Поэтому их можно записать сразу с учетом обозначений (8) в виде:

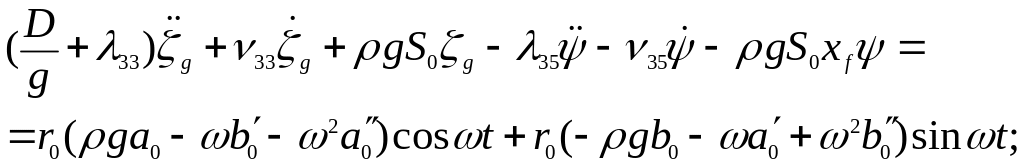(9)

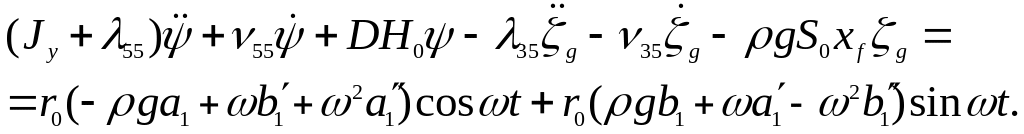(10)

Уравнение (9) – уравнение вертикальной качки корабля на волнении, уравнение (10) – уравнение килевой качки.

7.5. Уравнения продольной качки корабля, движуще- гося на встречном волнении. Решение уравнений

Левые части уравнений качки корабля, движущегося со скоростью , на тихой воде были получены в п. 7.3. Поскольку на волнении корабль качается с кажущейся частотой в левых частях уравнений качки будут стоять те же выражения для сил и моментов, но зависящие от , а в правых частях – выражения, полученные в п. 7.4. Коэффициенты правых частей не зависят от кажущейся частоты, так как они связаны с амплитудами волн, которые не должны меняться от присутствия волн. Тригонометрические функции будут зависеть от :

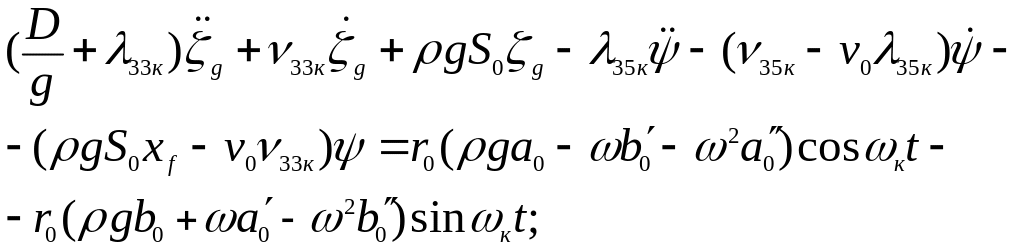(11)

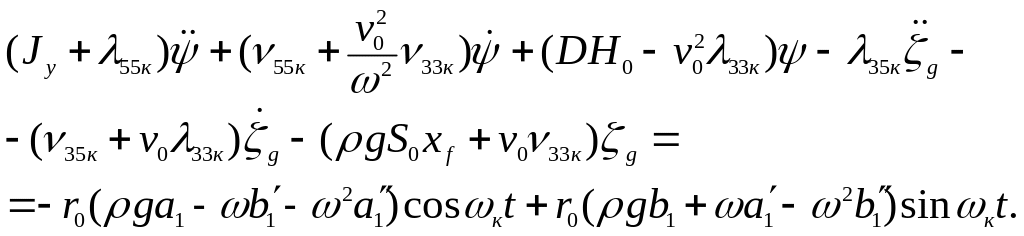(12)

Уравнения (11) и (12) являются обыкновенными линейными дифферен-циальными уравнениями 2-го порядка, неоднородными. Решения их ищутся в виде суммы 2-х решений: решения однородного уравнения (в правой части уравнения стоит 0) и решения неоднородного уравнения в форме правой части. Решения однородного уравнения быстро затухают, как мы это видели на примере бортовой качки на тихой воде, и остаются только решения в форме правых частей.

Правые части уравнений (11) и (12) можно представить в виде , поэтому решения их ищем в виде:

и (13)

После определения производных

; ;

; , (14)

подстановки их в уравнения качки и уравнивания коэффициентов отдельно при и при в левой и правой частях получится система четырех алгебраических уравнений для определения четырех неизвестных величин . Они будут иметь вид:

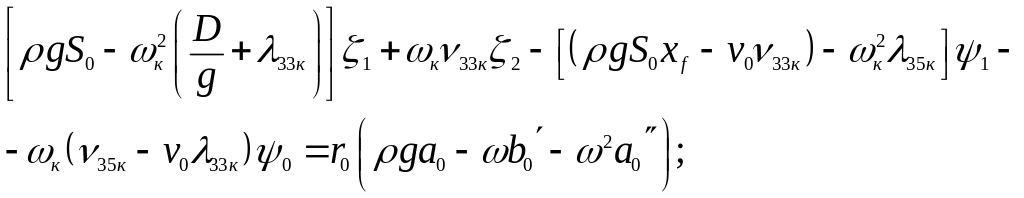
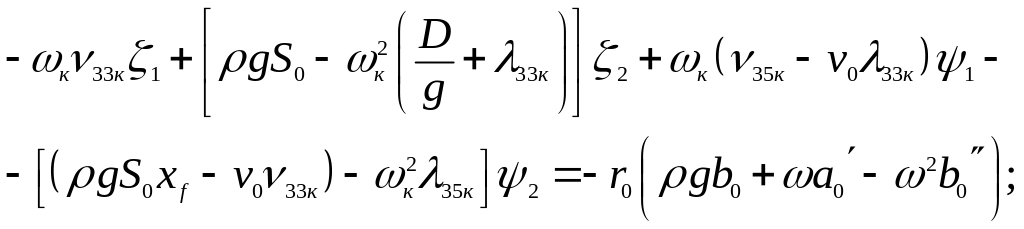
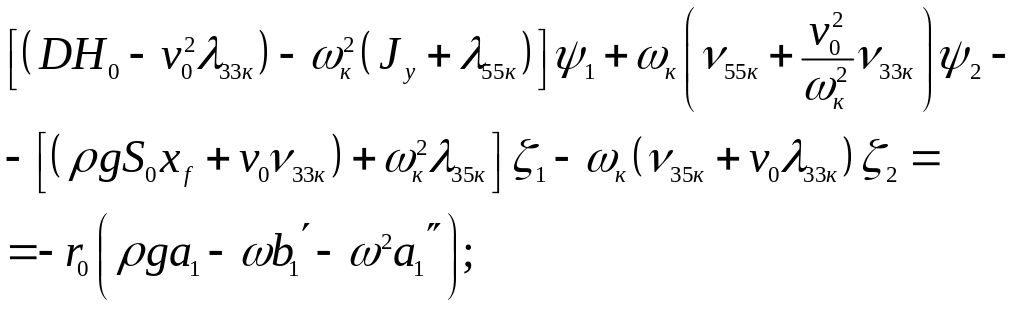
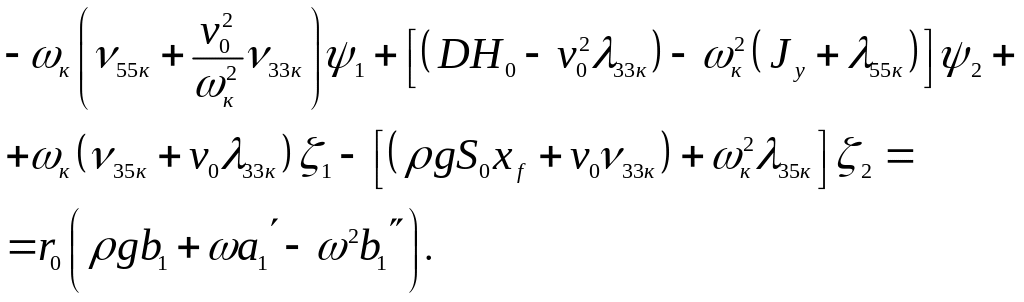(15)

Эта система уравнений решается каким-либо способом, например, с помощью определителей и т.д.

Выражения (13) можно представить в следующем одночленном виде :

(16)

Где - амплитуда вертикальной качки; (17)

-амплитуда килевой качки; (18)

-фаза вертикальной качки; (19)

-фаза килевой качки (20)

На рис.2 Представлены характерные амплитудно-частотные характеристики килевой и вертикальной качки контейнеровоза на различных курсовых углах. Видно, что эти кривые могут иметь резонансный характер , причем наиболее неблагоприятными являются встречные курсовые углы β=180 и β=135, где значения амплитудно-частотных характеристик достигают 1,5-2. На попутных курсовых углах β=0 и β=45 условие резонанса не выполняется, поэтому отсутствуют резонансные пики.

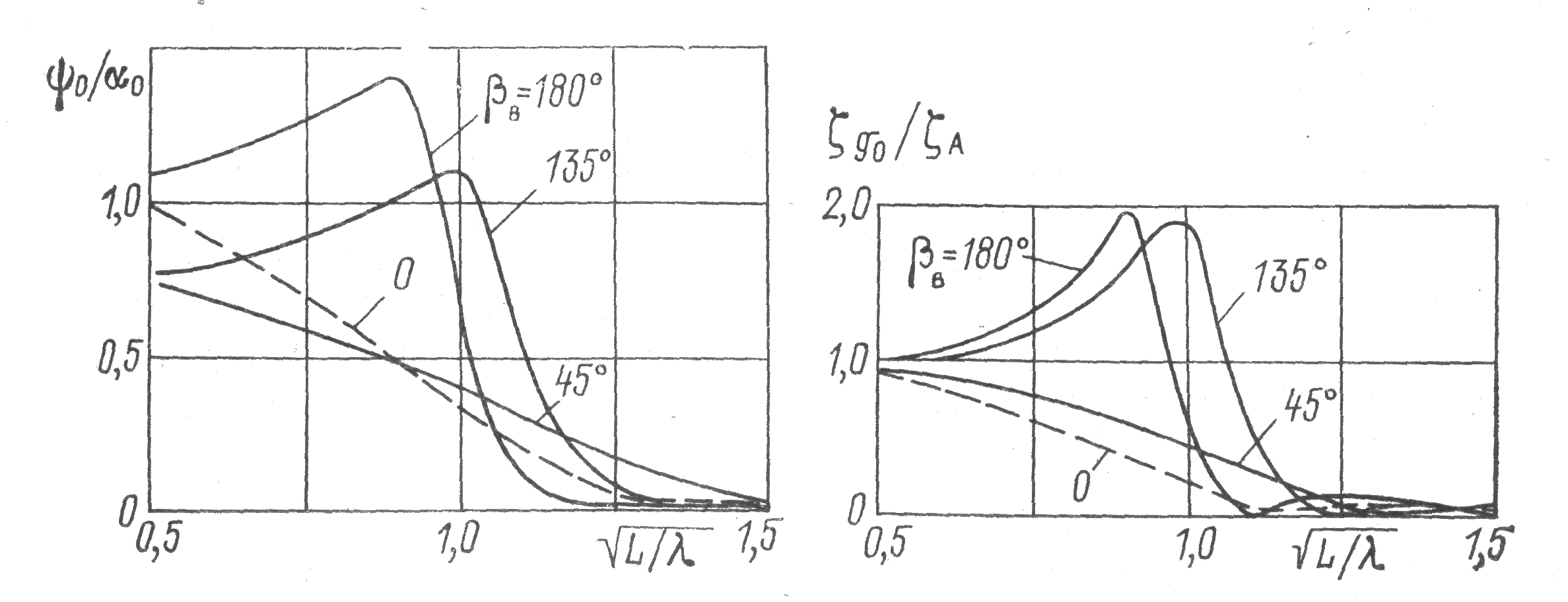
Рис.2 Амплитудно-частотные характеристики килевой и вертикальной качки контейнеровоза на различных курсовых углах.

После нахождения можно построить положения корабля на волнении для ряда моментов времени по формулам (13), и таким образом, увидеть как у корабля заливается палуба или оголяется днище (на рис. 3) затопленные участки палубы заштрихованы). При этом можно решить, как расставить надстройки и фальшборт, чтобы исключить заливание палубы, а также решить другие вопросы обитаемости. При оголении днища можно рекомендовать снизить скорость хода корабля.

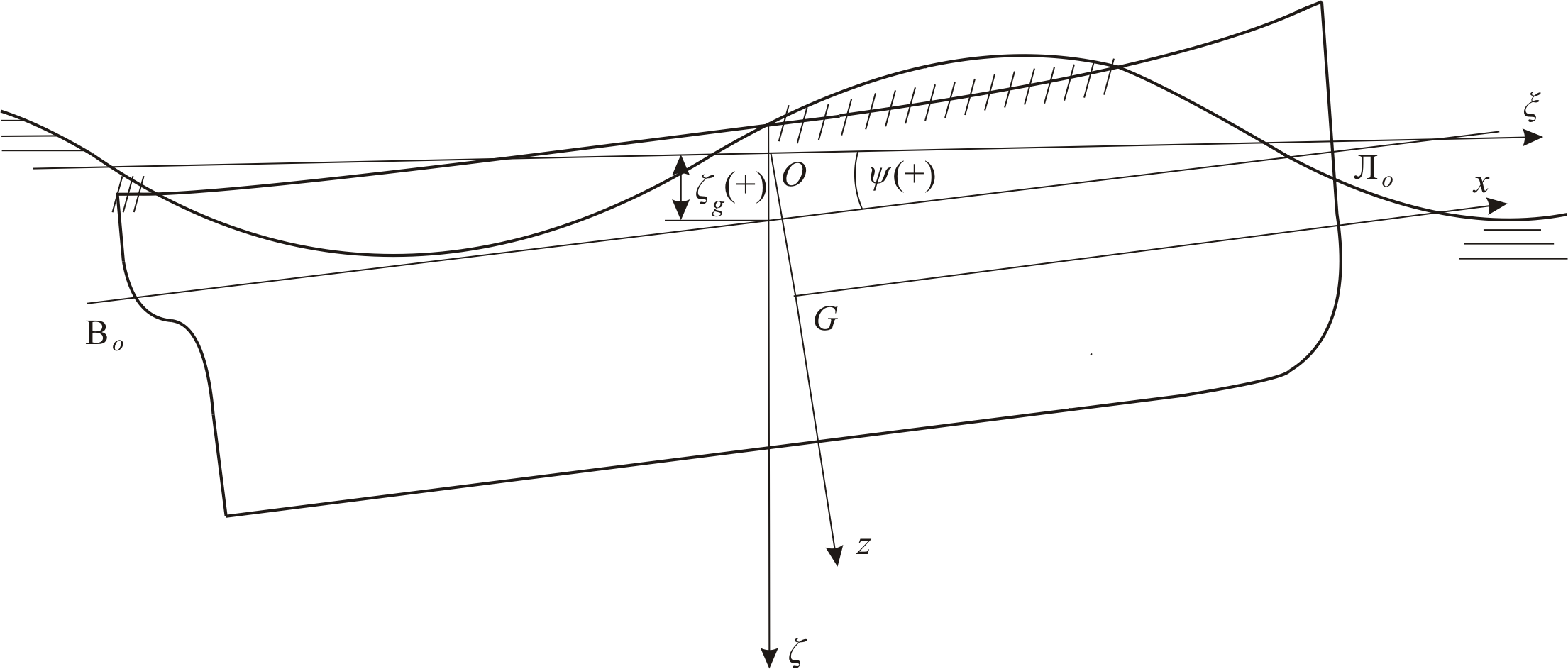
Рис. 3 К определению положения корабля на волнении