1) Решение исходной задачи как функция двух переменных разлагается в двойной ряд, т.Е. Представляется в виде:

С помощью процедуры ортогонализации Бубнова получим неоднородную систему алгебраических уравнений для определения коэффициентов разложения . Координатные функции удовлетворяют следующим условиям ортогональности:

Подстановка решения в исходное уравнение приводит к соотношению:

Проводим процедуру ортогонализации Бубнова: умножаем правую и левую части соотношения на и интегрируем по заданной области . Получим:

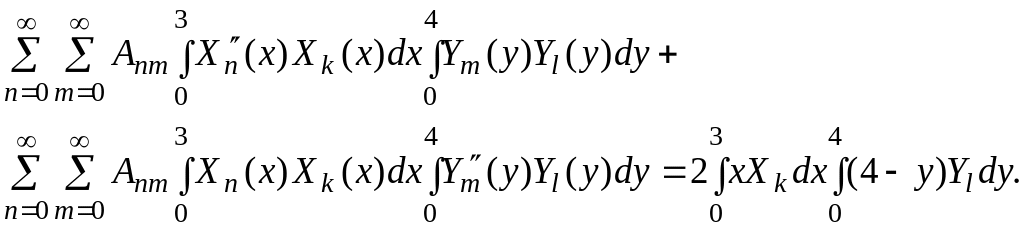
С учетом условий ортогональности используемых координатных функций получим:

Таким образом, решение краевой задачи в виде разложения в двойной тригонометрический ряд записывается в виде:

Величины вычисляются по формулам (4.7),(4.15).

2) Искомую функцию разлагают в ряд только по одному аргументу. Коэффициенты разложения при этом будут уже не числами, а функциями второго аргумента.

2А) Разложение функции в ряд по аргументу имеет вид:

Подстановка в исходное уравнение приводит к соотношению:

Проводим процедуру ортогонализации Бубнова: умножаем правую и левую части соотношения на и интегрируем по аргументу :

С учетом условий ортогональности используемых координатных функций получим:

Получили систему не связанных между собой неоднородных обыкновенных дифференциальных уравнений второго порядка с постоянными коэффициентами, решение каждого из которых представляется суммой общего решения однородного уравнения и частного решения неоднородного уравнения, вычисляемого методом подбора, т.е.

В записанном соотношении величины являются константами интегрирования и определяются из граничных условий задачи, а величины определяются при подстановке частного решения в рассматриваемое уравнение и приравнивании коэффициентов при одинаковых степенях .